Оценка успеваемости студентов по их среднему баллу, формируемому на основании оценок, получаемых при сдаче экзаменов, курсовых работ, зачётов с оценкой и т.д., является хорошим показателем, позволяющим оценить качество усвоения, и часто используется для выявления факторов, влияющих на успеваемость [1–8].
Для выявления причин, вызывающих демонстрацию студентами определённой средней успеваемости, широко применяются методы математической статистики [4–6]. Обычно для выявления связи между данными опросов (тестов, по которым определяются числовые характеристики параметров, предположительно влияющих на успеваемость) и успеваемостью используется различные методы корреляционного анализа. В работе [2, с. 46] отмечается: «Научный подход прежде всего предполагает создание в любой прикладной теории интуитивно понятного эмпирического базиса. Сложность, строгость и стоимость математического аппарата – так сказать, математической надстройки – должны сообразовываться с надёжностью базиса...». В соответствии с этим возникает вопрос о том, насколько информативен показатель средней успеваемости для целей выявления факторов, влияющих на успеваемость студентов.
Ранее [9] нами было показано, что переход от непараметрической статистики успеваемости отдельного студента к параметрической статистике успеваемости большой (> 100 человек) группы студентов оказывается не вполне тривиальным. Ограниченность диапазона допустимых значений средней успеваемости при приближении к границе приводит к возникновению функциональной зависимости между средней дисперсией в локальном интервале и средней успеваемостью в том же интервале. В связи с этим эффектом средние успеваемости, найденные для больших выборок студентов, не подчиняются нормальному закону распределения случайной величины, даже если изучаемое распределение прошло проверку при помощи критерия Хи-квадрат.
В свою очередь, это ставит под вопрос применимость множества статистических методов для интерпретации экспериментальных данных. В данной работе будет продолжен анализ успеваемости ранее полученной выборки студентов [9]. Для определённости напомним, что выборка состояла из студентов очной, заочной и дистанционной форм обучения (11 академических групп 2–4 курса, 108 человек), с количеством студентов в группе, случайным образом варьирующимся от четырёх до девятнадцати человек. Количество оценок, участвовавших в расчёте средней успеваемости отдельного студента, колебалось в интервале от тринадцати до сорока двух. Средняя успеваемость студентов в выборке оказалась равной четырём (с точностью до третьего знака после запятой).
Выявленные проблемы приводят к мысли о необходимости изменения методики анализа эмпирических данных по успеваемости студентов. Понятно, что было бы целесообразным уйти от необходимости осуществления перехода от непараметрической статистики успеваемости отдельного студента к параметрической статистике успеваемости большой группы студентов, от необходимости наложения ограничений на объём и (или) состав создаваемой выборки.
Ранее [9] нами было отмечено, что возможность пересдач на повышенную оценку маскирует реальную характеристику успеваемости студентов и приводит к снижению информативности обрабатываемых данных. Особенно этот фактор сказывается в области очень низких значений успеваемости. Конечно, желания пересдать на повышенную оценку могут возникать и у успевающих студентов, например отличников. В результате можно прийти к выводу о том, что оценка студента является некоторым консенсусом между реальным желанием студента получить определённую оценку и преподавателем, оценивающим, можно или нет поставить студенту желаемую им оценку.
Естественным способом преодоления выявленных проблем является использование вероятностных характеристик успеваемости, которые одинаковым способом рассчитываются как для отдельного студента, так и для большой выборки студентов. В связи с важностью показателя средней успеваемости используем этот параметр в качестве аргумента для функций вероятности получения определённой оценки. Поэтому вероятность получения студентом определённой оценки призвана не заменить, а раскрыть характеристику средней успеваемости, предоставить более информативные данные для сопоставления с результатами психолого-педагогических исследований. Для выполнения поставленной задачи были рассчитаны вероятности получения студентами каждой из возможных оценок. Иными словами, в работе проверялось наличие функциональной зависимости между средней успеваемостью и вероятностными характеристиками получения каждой из возможных оценок студентами использованной выборки.
Прежде всего, рассмотрим графики зависимостей вероятности получения студентами граничных зачётных оценок от средней успеваемости студента (рис. 1). Заметим, что графики пересекаются в области средней успеваемости анализируемой группы студентов. Каждый из графиков построен по всей выборке студентов. Из этого следует, что средняя успеваемость группы формируется усреднением двух тенденций, сосуществующих в каждом студенте. При этом уменьшение одной функции (например, вероятности получения отличной оценки) приводит к закономерному росту другой. На основании изложенного сразу возникает гипотеза о возможном существовании двух психологических характеристик, присущих каждому студенту и коррелирующих с представленными на рис. 1 зависимостями. Иными словами, можно сформулировать проблему нахождения двух-трёх психолого-педагогических характеристик, присущих каждому студенту, которые коррелируют с нисходящей и восходящей вероятностными функциями и имеют точку пересечения в области средней успеваемости изучаемой выборки студентов. При нахождении искомых психолого-педагогических характеристик можно, в свою очередь, предположить возможность прогнозирования успеваемости студентов на основании результатов тестирования. Впрочем, даже при нахождении таких характеристик для одной локальной выборки студентов ещё останутся вопросы относительно внешней валидности полученных результатов, так как имеется не исключаемая вероятность несовпадения факторных пространств, влияющих на изучаемые характеристики. Тем не менее, несмотря на наличие ряда проблем, предлагаемое представление успеваемости студентов может предоставить психологам и педагогам достаточно обширный материал для их творческих поисков и исследований.
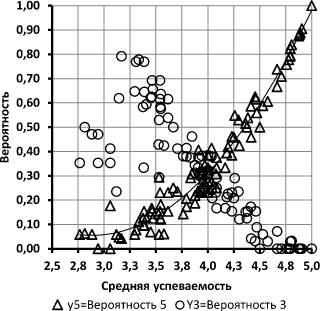
Рис. 1. Зависимости вероятностей получения удовлетворительной и отличной оценок от значения средней успеваемости студентов
После обсуждения общих вопросов, связанных с использованием вероятностных характеристик успеваемости студентов представляет интерес получить определённые численные характеристики представленных на рис. 1 зависимостей. Наименее проблематичной для целей трактовки полученных результатов выглядит зависимость вероятности получения отличной оценки, подчиняющаяся уравнению
Y5 = 0,2107x2 – 1,2258x + 1,8403. (1)
Заметим, что вероятность получения оценки «отлично» не равна нулю даже для очень слабо успевающих студентов. Это подтверждает наблюдение за тем, что у слабоуспевающих студентов может проявляться интерес к освоению отдельных дисциплин, или по каким-либо причинам, освоение некоторых дисциплин им даётся существенно легче. Очевидно, что эта особенность может представлять интерес для определения профориентации студентов. Тем не менее, даже проблематичные студенты не выпадают из общей зависимости распределения отличных оценок.
Вероятность получения удовлетворительной оценки имеет менее однозначный характер. Прежде всего, отметим, что в области слабых успеваемостей зависимость внезапно обрывается на уровне вероятности получения удовлетворительной оценки Y3 ≈ 0,8. Если принять во внимание, что даже для очень слабых студентов имеется отличная от нуля вероятность получения хороших и отличных оценок и что не все «двоечники» могут успеть пересдать неудовлетворительную оценку, то можно предположить, что значение вероятности получения удовлетворительной оценки никогда не достигнет сто – процентной отметки. Обращает на себя внимание то, что зависимость вероятности получения удовлетворительных оценок имеет тенденцию к разветвлению на две зависимости. Сопоставление с исходной выборкой показало, что нижняя ветвь (3) сформирована студентами со средней успеваемостью, близкой к трём баллам, и имеющими неудовлетворительные оценки по одному или нескольким предметам. Линии тренда ветвей, относящихся к вероятности получения оценок «удовлетворительно», описываются следующими уравнениями:
Y3в = 2,111 – 0,443x; (2)
Y3н = 0,735 – 0,114x. (3)
Зависимости (2) и (3) имеют точку пересечения, находящуюся в области средней успеваемости х = 4,18. Для полноты изложения отметим, что точка пересечения кривых, описываемых уравнениями (1)и (2) соответствует средней успеваемости х = 4,034, а кривые (1) и (3) пересекаются при х = 3,95. Иными словами, все точки пересечения лежат в области значений средней успеваемости изучаемой выборки студентов (х = 4,0021). Ещё раз отметим, что точки пересечения графиков могут быть реперными точками для сопоставления графиков, полученных при помощи различных тестов с характеристиками успеваемости.
Естественно, что изложенный материал является дискуссионным и требует дальнейших проверок. Вполне понятно, что если в дальнейшем будет подтверждено существование двух ветвей графика удовлетворительной успеваемости студентов, можно предполагать наличие различий и в факторном пространстве, описывающем мотивацию к обучению.
В отношении неудовлетворительных оценок отметим их нестабильность в количественном аспекте: их стараются побыстрее пересдать, либо стабильно неуспевающих студентов просто отчисляют. Таким образом, пересданные неудовлетворительные оценки пополняют график функции вероятности получения удовлетворительных оценок. Продолжая анализировать структуру средней успеваемости студентов, построим график вероятности получения студентами изучаемой выборки оценки «хорошо» (рис. 2), составляющей в нашем случае 28 % от общего количества оценок. Вид полученного распределения однозначно свидетельствует о том, что не имеет никакого смысла сопоставлять значения какого-либо фактора с вероятностью получения оценки «хорошо».
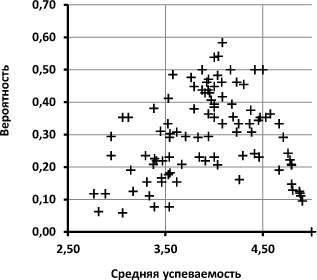
Рис. 2. Зависимость вероятности получения оценки «четыре» от средней успеваемости студентов
Полученная зависимость отражает тот факт, что оценка «хорошо» является компромиссной и имеет две фундаментальные тенденции: «четыре» ближе к «трём» или «четыре» ближе к «пяти». В результате можно заключить, что использование рассматриваемой методики вероятностного анализа успеваемости студентов предоставляет более информативный базис для педагогических исследований, так как в явном виде отражает тенденции к получению отличных и удовлетворительных оценок.
Например, в работе [8] изучалась связь ряда потенциально существенных факторов со средним баллом сессии, полученным студентом специальности «Статистика» за пятый семестр (2008/2009 г.). Полученные результаты показывают, что основное количество выявленных связей относится по уровню к слабых и очень слабых, лишь в отдельных случаях достигая умеренного и среднего уровня (рис. 3).
Обращает на себя внимание наличие отрицательных значений коэффициентов корреляции. Возможно, было бы интересно проследить, как изменились бы найденные связи, если вместо значений средней успеваемости использовать значения вероятностей получения отличных и удовлетворительных оценок. В связи с тем, что расчёт всех вероятностей вёдётся по всей выборке студентов, можно предполагать наличие потенциальной возможности выявления дополнительных факторов, способствующих переходу от тенденции снижения вероятности получения удовлетворительных оценок к повышению вероятности получения отличных оценок. Отметим, что выбор рассмотренного примера во многом случаен, но хорошо иллюстрирует суть обсуждаемой проблемы.

Рис. 3. Матрица парных корреляций [8]
Подводя итоги, можно отметить, что рассмотренная методика снимает проблемы предельного перехода, а также позволяет сделать предположение о том, что вероятностные характеристики успеваемости студентов являются более информативными, чем средняя успеваемость, и представляют интерес для более глубокого их изучения. Можно также предположить, что выделяемые на основании вероятностного анализа подклассы могут иметь собственные структуры факторного пространства, описывающего мотивацию к обучению студентов.
Рецензенты:
Долинер Л.И., д.п.н., заведующий кафедрой информационных технологий, ГБОУ ДПО «Институт развития образования», г. Екатеринбург;
Гребенников В.И., д.ф.-м.н., профессор, главный научный сотрудник, Институт физики металлов УрО РАН, г. Екатеринбург.
Работа поступила в редакцию 28.05.2014.
Библиографическая ссылка
Сосницкий В.Н., Потанин Н.И. ВЕРОЯТНОСТНЫЙ ПОДХОД К АНАЛИЗУ УСПЕВАЕМОСТИ СТУДЕНТОВ // Фундаментальные исследования. 2014. № 8-3. С. 734-738;URL: https://fundamental-research.ru/ru/article/view?id=34625 (дата обращения: 18.11.2025).



