Охрана здоровья населения требует не только совершенствования современных технологий при разработке лекарственных средств и внедрения перспективных методов лечения, но и, в первую очередь, поиска новых способов диагностики.
Данные статистики свидетельствуют, что, несмотря на наличие огромного практического опыта, экспериментальных исследований и разнообразия применяемых медикаментозных средств, число выявляемых заболеваний печени и осложнений после лечения не уменьшается. Среди основных причин такого положения можно выделить две: с одной стороны – высокая компенсаторная и адаптивная способность печени (заболевание выявляется на поздней стадии), с другой – проблемы объективности оценки состояния органа. Кроме того, тактика лечения выявленного заболевания, как правило, заключается в стимуляции восстановительных процессов – попытке реализовать обратное развитие изменений, которые по ходу заболевания сложились как компенсаторные или адаптивные [11]. Нередко лечение не приводит к желаемому результату, так как возврат к физиологической норме, в силу сложившегося морфофункционального соотношения и разной «подвижности» отдельных тканевых структур, сформировавшихся в процессе адаптивной реакции, невозможен. Таким образом, без учёта динамической составляющей тканевых процессов в органе такие действия могут приводить к ещё более тяжёлым последствиям и единственно возможным лечением в этом случае может оказаться хирургическое вмешательство.
Накопленный клинический опыт и экспериментальный материал являются основой для совершенствования существующих методов постановки диагноза и лечения печени [7]. Однако базируются они, как правило, на статических, в основном бинарных методах оценки показателей – позволяют определять две противоположные фазы – наличие активности процесса или стабильности и благоприятная тенденция или неблагоприятная. В этом случае сложно выявить закономерности динамики патологического процесса, что повышает вероятность ошибки в оценке состояния органа и делает используемые методы принятия решений не перспективными при разработке новых подходов к лечению заболевания. Действительно, диагноз, базирующийся на ограниченном количестве экспериментальных данных, подвергнутых в лучшем случае статистической обработке, не позволяет, например, оценить динамическую составляющую и выраженность реакции на повреждение, определить момент возникновения явления декомпенсации и начало перехода системы к адаптивной реакции – формированию нового стационарного состояния и оценить его устойчивость.
Разработка и внедрение перспективных методов лечения нуждается в новых подходах к исследованию состояния печени, учитывающих кинетику показателей, характеризующих её состояние. Реализовать такой подход можно только на базе математической модели, опирающейся на экспериментальные данные и отображающей зависимость показателей, характеризующих состояние системы, от степени интоксикации. Это позволит дать объективную характеристику состояния органа и создать основу для моделирования вариантов событий при разработке схем повышения функциональной активности органа [9; 10]. Однако исследование и оценка собственных, полученных в ходе эксперимента, и анализ литературных данных, свидетельствует о невозможности создания общей математической модели патологического процесса в широком диапазоне действия патологического фактора (от физиологического до терминального состояния) на базе дифференциальных уравнений или при помощи полиномиальных представлений [2; 3; 6; 9]. Это обусловлено тем, что в зависимости от морфофункционального состояния органа характер реакции системы на повреждение изменяется.
Цель исследования. С использованием новых подходов на базе экспериментальных данных создать математическую модель, позволяющую исследовать влияние степени интоксикации на морфофункциональные показатели печени. В основе такой модели должны лежать непрерывные зависимости, отображающие изменения отдельных показателей, что даёт возможность, используя аппарат математического анализа, оценивать не только такой очень важный параметр, как кинетика происходящих изменений, но и, по совокупности результатов исследования, состояние органа в целом. Это позволит не только повысить достоверность и точность определения текущего состояния органа, но и более основательно подойти к выработке стратегии и тактики лечения [5].
Материалы и методы исследования
В качестве модели патологии использована адекватная клиническим формам модель токсического гепатита, созданная введением тетрахлорметана (CCl4) в организм животного [4]. Экспериментальные исследования влияния степени интоксикации на печень проводились на крысах линии Вистар. Интоксикацию вызывали путём подкожного введения масляного раствора CCl4. В зависимости от тяжести моделируемого состояния вводили 4, 8, 20 и 64 инъекции тетрахлорметана. Исследования проводились на 1-е сутки после прекращения введения CCl4. В качестве контроля использовались интактные животные. Оценка общего состояния печени на разных стадиях повреждения, в процессе нарастающей степени интоксикации осуществлялась при помощи математической модели, позволяющей исследовать параметры динамики отдельных её показателей. Для математического моделирования были выбраны показатели, позволяющие дать объективную оценку состояния органа: относительная плотность волокнистой соединительной ткани (ОПСТ), число гепатоцитов (ГЕП), митотическая активность гепатоцитов (МИТ) и содержание гидрооксипролина (ОН-пр.). Информативность и точность оценок может быть повышена, если использовать дополнительную информацию – параметры, отражающие динамику процессов перекисного окисления липидов (ПОЛ) и функциональной активности органа.
Анализ данных базировался на основных принципах организации сложной живой системы:
1) любая реакция в самоорганизующейся системе направлена на обеспечение стационарности процессов;
2) максимальная функциональная активность органа может быть достигнута только в рамках стационарного состояния;
3) пока не исчерпан запас внутреннего противоречия, система стремится сохранять свою структуру и функцию.
Такой подход позволяет объяснить как состояние гомеостаза, так и возникновение компенсаторных явлений, роль адаптации.
В основе математической модели лежит аппроксимация экспериментальных данных непрерывными зависимостями вида «f = f(ССl4)», отражающими влияние степени интоксикации ССl4 на показатели печени «fi», определяющие стационарность её состояния и функциональную активность. Для решения этой задачи на этапе статистической обработки экспериментальных данных использовались пакеты статистических программ Microsoft Excel, Statistica 6.0 for Windows.Аппроксимация полиномиальными сплайнами выполнена с помощью системы компьютерной алгебры Mathcad 14 [1; 8; 12].
Результаты исследования и их обсуждение
Результаты исследований приведены в таблице.
Полученные путём аппроксимации непрерывные зависимости (полиномиальные сплайны) «fsp = fsp(ССl4)», отображающие изменения исследуемых показателей на высоте патологии (1-е сутки после прекращения введения CCl4), свидетельствуют об их полифункциональной зависимости от числа инъекций CCl4 (рис. 1-4, а). В совокупности со статистическим анализом они позволяют получить графическую информацию о влиянии числа введений CCl4 на показатели, характеризующие состояние системы. Однако без анализа данных, отражающих соответствующие изменения параметров их динамики, возможности такого анализа в значительной степени ограничены.
Морфологические данные, отражающие состояние печени
|
Число инъекций CCl4 |
МИТ (на 100 п/з) |
ГЕП (на 100 п/з) |
ОПСТ (усл. ед.) |
ОН-пр. (мкг/г) |
|
1 сут |
1 сут |
1 сут |
1 сут |
|
|
Контроль |
0,33 |
20,33 |
0,16 |
2,25 |
|
4 |
3,60 (р < 0,01) |
17,80 (р < 0,05) |
0,24 (р < 0,01) |
2,55 (р < 0,05) |
|
8 |
9,50 (р < 0,01) |
12,75 (р < 0,01) |
0,26 (р < 0,01) |
2,79 (р < 0,01) |
|
20 |
3,00 (р < 0,01) |
13,83 (р < 0,01) |
0,29 (р < 0,01) |
2,16 (р < 0,05) |
|
64 |
3,67 (р < 0,01) |
10,33 (р < 0,01) |
0,96 (р < 0,01) |
3,05 (р < 0,01) |
Примечание. Достоверность (p) рассчитана по отношению к контролю (Utest Маnn – Whitney); п/з – полей зрения.
Для исследования параметров динамики использовалась фазовая плоскость, на которой представлены зависимости
f(х) = dfsp/d(CCl4) и φ(х) = d2fsp/d(CCl4)2,
отражающие характер изменений исследуемых показателей под действием экзогенного фактора (CCl4) (рис. 1-4, б).
Зависимости вида f(х) = dfsp/d(CCl4) определяют чувствительность исследуемого параметра «fsp» к введению CCl4. Максимальное по модулю значение функции f(х) представляет интоксикацию, при которой происходят наиболее быстрые изменения исследуемого параметра.
Точка  , в которой выполняется условие
, в которой выполняется условие 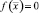 и при переходе происходит смена знака, является точкой экстремума (max или min)
и при переходе происходит смена знака, является точкой экстремума (max или min)
зависимости fsp = fsp(ССl4).
а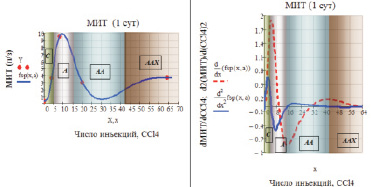 б
б
Рис. 1. а – зависимость числа митозов (МИТ) от степени интоксикации CCl4 (аппроксимация сплайнами); б – динамика показателей митотической активности (МИТ) в зависимости от степени интоксикации CCl4: d(МИТ)/d(CCl4) и d2(МИТ)/d(CCl4)2. (С, А, АА, ААХ – обозначения зон стационарности митотической активности гепатоцитов)
Кроме того, если в точке  выполняется условие
выполняется условие 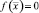 , то в окрестности этой точки возможны три случая [9]:
, то в окрестности этой точки возможны три случая [9]:
1. Переход функции f(х) через нулевое значение со сменой знака с «+» на «–».
2. Переход f(х) через нулевое значение со сменой знака с «–» на «+».
3. Приближение f(х) к нулевому значению из области без смены знака.
Ситуация, оцениваемая, как показано в первом случае, свидетельствует, что исследуемый параметр, находится в устойчивом стационарном состоянии, которое обеспечивается в системе (в активной среде), где протекает множество процессов, в том числе и разнонаправленных, превалирует отрицательная обратная связь (ООС). Во втором – параметр находится в неустойчивом стационарном состоянии. Это может быть следствием того, что ООС в системе слаба или отсутствует и преимущественным является действие положительной обратной связи (ПОС). Это не способствует стабилизации состояния и с изменением переменной х будет происходить удаление исследуемого параметра от стационарного состояния. В третьем случае оцениваемый параметр также находится в неустойчивом стационарном состоянии, представлена ситуация монотонного приближения к области, где действие патогенного фактора уже не оказывает значимого влияния на исследуемый параметр, так как система уже не обладает достаточным ресурсом для обеспечения функциональной активности органа.
а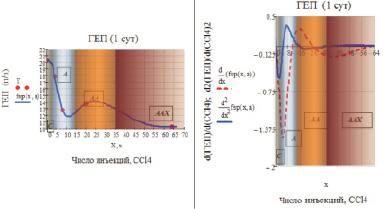 б
б
Рис. 2. а – зависимость числа ГЕП от степени интоксикации CCl4 (аппроксимация сплайнами); б – динамика показателей числа ГЕП в зависимости от степени интоксикации CCl4: d(ГЕП)/d(CCl4) и d2(ГЕП)/d(CCl4)2. (С, А, АА, ААХ – обозначения зон стационарности числа гепатоцитов)
а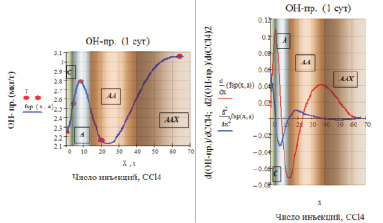 б
б
Рис. 3. а – зависимость содержания Он-пр. от степени интоксикации CCl4 (аппроксимация сплайнами); б – динамика показателей содержания Он-пр. в зависимости от степени интоксикации CCl4: d(ОПСТ)/d(CCl4) и d2(ОПСТ)/d(CCl4)2. (С, А, АА, ААХ – обозначения зон стационарности содержания гидрооксипролина – ОН-пр.)
а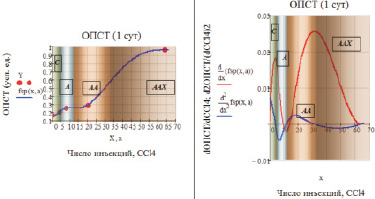 б
б
Рис. 4. а – зависимость ОПСТ от степени интоксикации CCl4 (аппроксимация сплайнами); б – динамика показателей ОПСТ в зависимости от степени интоксикации CCl4: d(ОПСТ)/d(CCl4) и d2(ОПСТ)/d(CCl4)2. (С, А, АА, ААХ – обозначения зон стационарности относительно плотности волокнистой соединительной ткани – ОПСТ)
Функции φ(х) = d2fsp/d(CCl4)2 также являются важным аналитическим инструментом, они позволяют исследовать интенсивность реакции системы, а следовательно, оценить соотношение действующих в системе «сил-антагонистов», обеспечивающих её стационарное состояние. Так, условие (φ(х) = 0) позволяет найти точки перегиба графика исследуемой зависимости, что можно охарактеризовать как момент наступления явления декомпенсации при сложившейся морфофункциональной организации печени. Это явление возникает в силу ограниченности ресурса системы, оно приводит к нелинейности ответной реакции и является началом выхода её из сложившегося стационарного состояния. Условие, когда функция φ(х) = max(min), позволяет оценить интенсивность реакции системы на действие патогенного фактора. Действительно, чем больше значение φ(х) в области стационарности, тем интенсивнее реакция активной среды, тем больше затрачивается энергии для обеспечения стационарного состояния органа. Условие φ(х) < 0 относится к области устойчивого, а φ(х) > 0 области неустойчивого стационарного состояния системы. Аппарат математического анализа даёт возможность оценить интенсивность реакции активной среды на повреждение; границы степени интоксикации, в рамках стационарного состояния, в пределах которых наблюдается компенсаторная реакция печени; степень интоксикации, при которой компенсаторная реакция органа становится недостаточной (условия возникновения декомпенсации); условия формирования нового стационарного состояния и ресурсную базу для его обеспечения.
Как показано на рис. 1–4, а, введение тетрахлорметана вызывало сложную реакцию живой системы, сопровождавшуюся изменением митотической активности, числа гепатоцитов состояния соединительной ткани.
Используя математические представления (условие: f(х) = (dfsp/d(CCl4)) = 0 и φ(х) = (d2fsp/d(CCl4)2) = 0), можно выделить несколько зон: С, А, АА и ААХ (на рис. 1-4 они окрашены в разные цвета), оцениваемых по числу инъекций CCl4, при которых состояние исследуемого показателя можно охарактеризовать как стационарное. Из представленных данных (ГЕП, МИТ, ОПСТ, ОН-пр.) следует, что с ростом степени интоксикации первая недостаточность компенсаторной реакции систем органа возникает в области от 4 до 5 инъекций CCl4 (зона С – физиологическое состояние). Практически это тот «рубеж» (левая граница), после которого начинает формироваться новое стационарное состояние – хроническое (зона А – адаптивная реакция). Правая граница этой зоны находится в области 15–18 инъекций тетрахлорметана. Анализ представленных на рис. 1–4 данных, отражающих состояние основных показателей печени на высоте патологии, позволяет сделать вывод, что для МИТ, ОПСТ и ОН-пр. в зоне (А) наблюдается устойчивое стационарное состояние, для ГЕП – состояние неустойчивое.
Дальнейший рост степени интоксикации приводит к тому, что в области 16–18 инъекций CCl4 возникает недостаточность компенсаторной реакции – зона А. В результате начинает формироваться новое стационарное состояние – зона АА. Верхняя граница этой зоны в значительной степени «размыта» и находится в области 32–39 инъекций CCl4. На высоте патологии в зоне АА из представленных показателей в устойчивом стационарном состоянии находится только ГЕП. Общее состояние системы в зоне АА можно охарактеризовать как стационарное на грани устойчивости, так как в этой зоне наблюдается снижение МИТ и увеличение ОПСТ. Недостаточность энергии, слабая ООС или полное её отсутствие приводят к тому, что дальнейшее увеличение степени интоксикации вызывает нарастающую деградацию системы, вплоть до полного её разрушения. Действительно, при достижении верхней границы зоны АА (32–39 инъекций CCl4) система переходит в новое состояние – зону ААХ, назвать которое стабильным уже нельзя, поскольку ни один из исследуемых показателей не находится в устойчивом стационарном состоянии (рис. 1–4). Кроме того, на фоне низкой МИТ, снижения ГЕП наблюдается быстрый рост ОПСТ. Это свидетельствует о том, что система уже не имеет ресурса не только для обеспечения стационарности состояния, но и функциональной активности органа. На этой стадии наблюдалась гибель значительного числа исследуемых животных.
Заключение
Проведённый анализ свидетельствует, что обнаруженные с использованием математической модели закономерности, отражающие объективные процессы, вызванные действием патогенного фактора, позволяют определить степень интоксикации, при которой наступает декомпенсация системы, а также границы в которых её состояние можно оценить как стационарное. Кроме того, такой подход позволяет исследовать значения и динамику отдельных показателей, на основе которых формируется состояние органа и их соотношения. Математическое моделирование позволяет также установить один из важнейших показателей, отображающий реактивность живой системы – характер действующей обратной связи, оценить устойчивость параметров и процессов, обеспечивающих стационарное состояние системы в широком диапазоне действия патогенного фактора (от физиологического до терминального состояния).
Рецензенты:
Шатров А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования, ФГБОУ ВПО «Вятский государственный университет», г. Киров;
Спицын А.П., д.м.н., профессор, заведующий кафедрой патофизиологии, ГБОУ ВПО «Кировская государственная медицинская академия» Министерства здравоохранения Российской Федерации, г. Киров.
Работа поступила в редакцию 07.03.2014.
Библиографическая ссылка
Кудрявцев В.А., Косых А.А., Цапок П.И. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМНО ОРГАНИЗОВАННЫХ ПРОЦЕССОВ В ПЕЧЕНИ ЖИВОТНОГО ПРИ ИНТОКСИКАЦИИ ТЕТРАХЛОРМЕТАНОМ // Фундаментальные исследования. 2014. № 5-6. С. 1201-1206;URL: https://fundamental-research.ru/ru/article/view?id=34067 (дата обращения: 16.01.2026).



