Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лелявин К.Б. 1 Аникин А.С. 2 Горнов А.Ю. 2

---

1 ГБОУ ВПО «Иркутский государственный медицинский университет»

2 Институт динамики систем и теории управления СО РАН

Проведено одноцентровое, рандомизированное, открытое, ретроспективное, обсервационное, когортное клиническое исследование, в котором приняли участие 896 больных мышечно-неинвазивным (Та, Т1 и Тis) раком мочевого пузыря. Из них у 256 (28,6 %) пациентов (группа А) применены биполярные технологии эндоуретрального удаления опухолей мочевого пузыря в 0,9 % растворе NaCl (TURis-vap), а 640 (71,4 %) больных (группа Б) были оперированы с помощью эталонного метода – монополярной трансуретральной резекции и вапоризаци (TUR-vap) опухоли мочевого пузыря. Проанализированы возможности и ограничения использования метода Шепарда для моделирования рисков хирургического лечения рака мочевого пузыря. Для ряда показателей (общее число осложнений) модели имеют довольно хорошие характеристики при минимальном объеме «чистки». Для других показателей (срок возникновения рецидивов) модели аппроксимации по Шепарду имеют весьма низкое качество и требуют гораздо более тщательной процедуры обработки исходных данных. Проведение процедуры «чистки» позволяет существенно повысить точность работы созданных моделей аппроксимации по Шепарду. Для достижения приемлемой точности (≥80 %) в среднем потребовалось удаление порядка 40 % данных исходных выборок. Проведение дальнейшей чистки позволяет создавать модели, имеющие точность работы, превосходящую 95 %.

Статья в формате PDF

908 KB

мышечно-неинвазивный рак мочевого пузыря

эндоуретральное хирургическое лечение

метод Шепарда

1. Аляев Ю.Г., Рапопорт Л.М., Цариченко Д.Г., Калантаров Р.А. Опыт использования биполярной трансуретральной резекции в лечении поверхностных опухолей мочевого пузыря // Онкоурология. – 2009. – № 1. – С. 32–34.

2. Аникин А.С. Решение задачи факторного анализа с использованием аппроксиманта Шепарда // Ляпуновские Чтения. Презентация информационных технологий. Материалы конференции. – Иркутск, 2008. – С. 1–2.

3. Горнов А.Ю., Кузьменко Е.Т., Аникин А.С., Зароднюк Т.С. Применение алгоритмов аппроксимации экспериментальных данных в задаче выявления значимых медико-социальных факторов // Современные технологии. Системный анализ. Моделирование. – Иркутск: ИрГУПС, 2008. – Спец. выпуск. – С. 92–96.

4. Калантаров Р.А. Биполярная трансуретральная резекция при раке мочевого пузыря: автореф. дис …канд. мед. наук: 14.01.23. – М., 2010. – 27 с.

5. Клиническая онкоурология / под ред. проф. Б.П. Матвеева. – М.: Издательский дом «АБВ-пресс», 2011. – 934 с.

6. Кузьменко В.В., Аникин А.С., Горнов А.Ю. Оценка точности математических моделей расчета концентраций фракций холестерина // Бюллетень ВСНЦ СО РАМН. – 2010. – № 4. – C. 185–189.

7. Математический энциклопедический словарь. – М.: Большая Российская энциклопедия, 1995.

8. Переверзев А.С. Опухоли мочевого пузыря / А.С. Переверзев, С.Б. Петров. – Xарьков: Изд-во Факт, 2002. – 303 с.

9. Умеров А.Н., Шуршев В.Ф. Методы и программны Вестник Астраханского технического университета. – 2005. – № 1. – С. 97–104.

10. Shepard D. A two-dimensional interpolation function for irregularly-spaced data. Proc. of the 23 ACM National Conference. N.Y.: ACM Press, 1968. pp. 517–524.

Современный уровень развития медицинской науки, в частности, онкологии, требует проведения широкомасштабных междисциплинарных клинических исследований и связан с обработкой большого количества результатов (показателей, факторов) диагностики и лечения заболеваний, которая не представляется возможной без применения современных средств вычислительной техники и соответствующих методов анализа имеющихся данных [2; 3; 6; 9].

Рак мочевого пузыря (РМП), являясь распространенным урологическим заболеванием, по-прежнему привлекает пристальное внимание ученых во всем мире, так как вопросы диагностики и лечения данного заболевания и сегодня далеки от окончательного решения.

Основным и первым этапом в диагностике и лечении мышечно-неинвазивным РМП является монополярная трансуретральная резекция (ТУР) опухоли мочевого пузыря (МП), признанная во всем мире эталонным (стандартным) методом лечения заболевания [5; 8]. Однако, несмотря на все преимущества, монополярная ТУР не может претендовать на исключительную роль в лечении описываемой патологии [5; 8]. В последние годы в эндоуретральной хирургии прочные позиции заняла биполярная трансуретральная резекция (TURis) в 0,9 % растворе NaCl [5; 8]. Количество исследовательских работ, в которых оценивались возможности нового описанного выше метода эндоуретрального лечения мышечно-неинвазивного РМП, в том числе непосредственные и отдаленные результаты лечения пациентов, незначительное [1; 4].

Накапливаемые данные и разрабатываемые методики их обработки открывают перед клиническими исследователями широкие возможности для решения медицинских задач различного уровня сложности. Однако разнородность имеющейся информации и многообразие методов ее обработки заметно усложняют процесс анализа и сопоставления получаемых результатов лечения больных.

На данный момент в хирургии РМП нет методик, позволяющих с высокой степенью достоверности принимать правильное решение в лечебной тактике у конкретного больного на основе моделирования рисков и исходов оперативного лечения. Перспектива использования метода D. Shepard при моделировании и анализе клинических медицинских данных, в частности, у больных РМП для прогнозирования рисков и контроля эффективности эндоуретрального хирургического лечения описываемой патологии является актуальной и перспективной проблемой, требующей изучения.

Цель исследования: проанализировать возможности и ограничения использования методик аппроксимации по D. Shepard для моделирования рисков и исходов различных видов эндоуретрального хирургического лечения больных мышечно-неинвазивным раком мочевого пузыря.

Материалы и методы исследования

Поставленная задача была реализована в рамках одноцентрового, рандомизированного, открытого, ретроспективного, обсервационного, когортного клинического исследования, в котором приняли участие 896 пациентов, страдающих РМП (Та, Т1 и Тis) находившихся на оперативном лечении в урологическом отделении ГБУЗ «Областной онкологический диспансер» г. Иркутскав период с 2000 по 2011 гг., главный врач – докт. мед. наук, профессор В.В. Дворниченко

Согласно критериям включения и учетом вида использованного эндоуретрального хирургического вмешательства полученная выборка рандомизировалась на 2 клинические группы. В основную группу (далее А) вошли 256 (28,6 %) больных, оперированных с использованием биполярных технологий эндоуретрального удаления опухоли МП – трансуретральной резекции (TURis) и электровапоризации (vap) в 0,9 % растворе NaCl (UES-40 Surg. Master, Olympus). В группу клинического сравнения (далее Б) вошли 640 (71,4 %) пациентов, оперированных с использованием эталонной техники эндоуретрального удаления опухолей МП – монополярной трансуретральной резекции (TUR) и электровапоризации (vap) (Autocon, серии 350, Karl Storz). Для снижения риска рецидивирования и прогрессирования РМП в исследуемых группах после операции (при отсутствии противопоказаний) проводилась адьювантная внутрипузырная лекарственная химио- или иммунотерапия в монорежиме. Адьювантная внутрипузырная лекарственная терапия выполнялась немедленно (доксорубицин – 50 мг, митомицин С – 40 мг) или отсроченно (вакцина БЦЖ «Имурон») после оперативного лечения с обязательным учетом объективных данных о распространённости РМП (данных патологоанатомического исследования), радикальности хирургического вмешательства и анализа прогностических факторов течения заболевания. В зависимости от вида адьювантной внутрипузырной лекарственной терапии среди больных мышечно-неинвазивным РМП в каждой группе (А и Б) было выделено по 4 подгруппы. Стандартный план обследования и показания к выполнению операции определяли согласно рекомендациям Европейской ассоциации урологов. Распределение по группам и подгруппам изучаемой выборки больных РМП представлено в табл. 1.

Под аппроксимацией понимается замена одних математических объектов другими, в том или ином смысле близких к исходным [7]. В данном случае широкое понятие аппроксимации использовано в узком смысле – как «восстановление функциональной зависимости по клиническим данным, полученным в ходе исследования эффективности эндоуретрального хирургического лечения 896 больных мышечно-неинвазивным РМП».

Таблица 1

Распределение пациентов, включенных в исследование, по группам и подгруппам, абс. / %

Моделирование является частью клинического исследования, ставящей целью использование построенной модели для практического применения (обобщения клинических данных, выявления значимых факторов процессов, построения моделей для дальнейшего прогнозирования и др.) или для дальнейшего развития какой-либо теории медико-биологической науки.

Для решения рассматриваемой задачи был применен метод создания статических моделей с использованием оператора D. Shepard [10], который предполагает построение интерполянта в виде отношения двух дробно-рациональных функций, опирающихся на клинические данные (обучающую выборку), полученных при изучении эффективности эндоуретрального хирургического лечения мышечно-неинвазивного РМП.

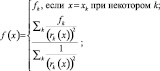
где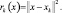

Метод Шепарда, идеологически близкий к методу обратных расстояний и методу радиально-базисных функций, которые широко применяются в нейромоделировании, достаточно редко используется для задач, связанных с анализом клинических данных. Изначально метод был создан для обработки картографической информации, но его возможности, по нашему мнению, гораздо шире. К достоинствам метода следует отнести невысокую вычислительную сложность, что позволяет с успехом применять его для обработки больших массивов экспериментальных данных, содержащих тысячи и десятки тысяч показателей и прецедентов.

Используя принцип тестирования данных на самих себе («метод комитетов»), из исходных данных, полученных при лечении больных РМП, сформированы две выборки – обучающая и тестирующая. На обучающей части выборки при помощи технологии D. Shepard строилась аппроксимирующая функция, а тестирующая выборка использовалась для оценки качества этой функции.

Тестирование сводилось к процедуре оценки значения функции в каждой точке тестирующей выборки и вычисления среднего и максимального «разброса». Для того, чтобы результаты такого тестирования можно было считать достаточно правдоподобными, исходные данные случайным образом разбиваются в пропорции 80/20, где 80 % попадают в обучающую выборку, а 20 % ‒ в тестирующую, а процедура тестирования повторяется достаточно большое количество раз (например, 1000). Погрешность построенной модели в процентах оценивается по формуле 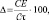где CЕ – число «число промахов» (неудачных точек аппроксимации), Сτ – число элементов обучающей выборки. Естественно считать, что чем меньше данная величина, тем более точной является построенная аппроксимация.

В ретроспективном массиве описание каждого больного РМП состояло из значений 190 переменных, содержащих ряд ключевых признаков: паспортные данные, пол, возраст, факторы риска, данные анамнеза и результаты проведенных инструментальных методов исследования, наличие сопутствующих заболеваний, клинико-морфологические признаки злокачественного новообразования (размер опухоли, ее локализация и характер роста, степень распространенности заболевания по системе TNM, гистологическая структура опухоли и ее гистопатологическая градация), вид проведенного эндоуретрального лечения и последующей адъювантной внутрипузырной терапии, непосредственные и отдаленные результаты лечения.

На первом этапе предлагаемой методики оказалось целесообразным выявить элементы обучающей выборки (прецеденты), вносящие наибольший «шум» в генерируемые модели, произвести «чистку» исходных данных по горизонтали.

На основе исходных данных больных мышечно-неинвазивным РМП были созданы три обучающие выборки: все больные, включенные в исследование (n = 896); основная группа больных (группа А) и группа клинического сравнения (группа Б).

В дальнейшем для каждой такой выборки были созданы модели из интересующих нас показателей: длительность эндоуретрального вмешательства (мин.); общее число интра- и послеоперационных осложнений; общее количество рецидивов опухоли МП; длительность безрецидивного периода (мес.) и общая пятилетняя выживаемость (да/нет).

Для оценки качества построенных моделей применялся метод комитетов, заключающийся в том, что для каждого элемента выборки проводился расчет значения интересующего нас показателя при помощи многомерной аппроксимирующей функции, построенной методом Шепарда на всех остальных элементах исходной выборки. Поскольку истинные значения показателя для всех таких элементов известны, становится возможным вычислить погрешность проводимого расчета и, соответственно, погрешность всей модели. При оценке погрешности модели учитывается количество элементов выборки, для которых вычисленное значение показателя отличается от истинного не более, чем на заданное отклонение Δmax.

В данной работе производилось удаление до 90 % исходных данных для получения более общей информации о поведении моделей. Одним из разумных критериев может быть удаление минимального количества элементов выборки, которое обеспечивает требуемое качество работы модели. Алгоритмы, реализующие предложенные подходы и методики, реализованы на языке C++ и функционируют под операционными системами семейств Linux, Windows и Mac OS X.

Результаты исследования и их обсуждение

По результатам проведенных вычислительных экспериментов были получены следующие данные.

Из приведенных в табл. 2 данных очевидно, что качество работы моделей является неудовлетворительным, что однозначно сигнализирует о необходимости предварительной обработки исходных данных.

По опыту предыдущих работ было принято решение о проведении так называемой «горизонтальной чистки», заключающейся в постепенном удалении элементов выборки, которые вносят большой шум, т.е. увеличивают погрешность модели. Выполнение данной операции позволяет в большинстве случаев существенно повысить качество модели. Максимальное количество удаляемых при «чистке» элементов может быть различным – это зависит от выбранной стратегии и постановки задачи.

Таблица 2

Обучающие выборки и точность методик аппроксимации по D. Shepard, %

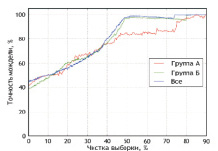
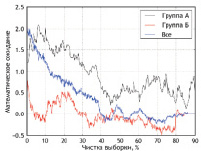
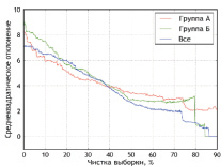
Рис. 1. Многомерные аппроксимирующие функции по признаку длительность эндоуретрального хирургического вмешательства, Δmax = 5 мин

Выводы

Установлено, что поведение различных моделей аппроксимации по D. Shepard отличается существенным образом. Для ряда показателей (общее число осложнений) модели имеют довольно хорошие характеристики при минимальном объеме «чистки». Для других показателей (срок возникновения рецидивов) модели аппроксимации по D.Shepard имеют весьма низкое качество и требуют гораздо более тщательной процедуры обработки исходных данных.

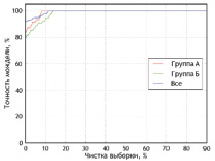
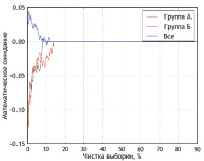
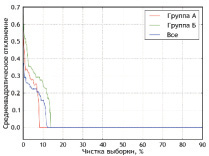
Рис. 2. Многомерные аппроксимирующие функции по признаку «общее число интра- и послеоперационных осложнений», Δmax = 0,5

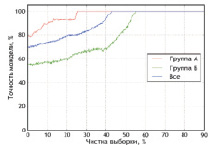
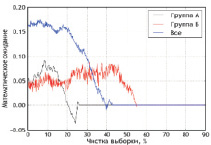
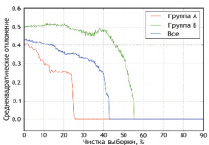
Рис. 3. Многомерные аппроксимирующие функции по признаку «общее количество рецидивов», Δmax = 0,5

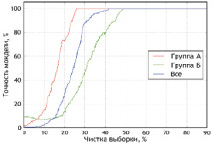
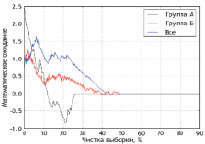
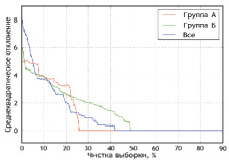
Рис. 4. Многомерные аппроксимирующие функции по признаку «длительность безрецидивного периода», Δmax = 1 мес

Таблица 3

Точность моделей аппроксимации по D. Shepard

Проведение процедуры «чистки» позволяет существенно повысить точность работы созданных моделей аппроксимации по D. Shepard. Для достижения приемлемой точности (≥ 80 %) в среднем потребовалось удаление порядка 40 % данных исходных выборок. Проведение дальнейшей чистки позволяет создавать модели, имеющие точность работы, превосходящую 95 %.

Оценка в 40 % «чистки» выборок свидетельствует как о сложности постановки задачи, так и необходимости более тщательного анализа исходных данных. В дальнейших исследованиях планируется применение различных методов кластерного анализа и ряда других подходов, направленных на декомпозицию исходной задачи для создания более адекватных моделей исследуемой предметной области.

Рецензенты:

Куклин И.А., д.м.н., ведущий научный сотрудник, ФГБУ НЦРВХ СО РАМН, г. Иркутск;

Зеленин В.А., д.м.н., ведущий научный сотрудник, ФГБУ НЦРВХ СО РАМН, г. Иркутск.

Работа поступила в редакцию 21.12.2013.

Библиографическая ссылка