Цель исследования. Схемы территориального планирования разрабатываются для систем расселения различных масштабов: государственный, субфедеральный, региональный, муниципальный. Агломерационная форма расселения ставит задачу разработки для себя аналогичных схем.
Территориальное планирование агломераций призвано максимизировать синергетический эффект, получаемый от взаимодействия частей городской агломерации (Далее – ГА). При неграмотном расположении населенных пунктов в агломерации, при превышении порога её численности наступает эффект дезэкономии. Он опасен не только для самой ГА, но и для региона (эффект «опустынивания»).
Соответственно для предотвращения возникновения эффекта дезэкономии важно оптимально спланировать в ГА расположение одних городов относительно других, плотность населения, расположение транспортной и иной инфраструктуры.
Необходимо наличие теории пространственного развития, отвечающей на следующие вопросы:
1. Определение границ (делимитация) ГА.
2. Построение оптимальной агломерационной системы для избегания образования гигантских мегалополисов и «схлопывания» экономики региона.
3. Выявление оптимальных мест для застройки, расположения промышленности, зеленых зон и иных объектов внутри ГА.
Решению вопроса оптимального расселения населения посвящено сразу несколько моделей города и систем городов.
Антология исследования
Для единичного города выделяют пять моделей города:
- Изолированное государство фон Тюнена (поясная структура города; конец 19 в. – нач. 1930-х гг.).
- Концентрическая модель Бёрджеса (расширение зон по направлению к периферии; 1925 г.).
- Секторная модель Хойта (радиальная модель города с секторальными вставками (вдоль дорог и т.п.), т.е. комбинация секторального подхода и модели фон Тюнена; с 1931 г.).
- Многоядерная модель Ульмана-Харриса (многоядерная, в городе несколько центров; c 1946 г.).
- Факторная экология.
Для систем городов существует пять моделей системы городов:
- Модель центральных мест Кристаллера – Лёша (пригодна для нескольких городов и позволяет построить модель каркаса городов; 1930–1950-е г.).
- Правило Ципфа.
- Диффузия нововведений Хагерстранда (процесс не охватывает всю территорию сразу, а возникает сначала в неких точках и распространяется отсюда по неким законам, упорядоченно).
- Гравитационные модели и теория поля потенциалов (позволяет построить модель двух городов, когда их влияние различно по силе; но эту модель сложно распространить на число городов более двух; псевдоаналогия с законом Ньютона-Кулона).
- Географическая теория поля или модель потенциалов Кларка-Медведкова (потенциал точки равен сумме отношений людности каждого города к расстоянию от него до данной точки).
Так или иначе, но каждая из перечисленных моделей обладает рядом недостатков:
- существенные ограничения в применимости по отношению к крупным системам расселения, объединяющим более двух городов;
- не учитывают влияние географических объектов на развитие города;
- нет увязки развития систем городов в контексте развития всего региона.
Материал и методы исследования
Мы предлагаем использовать принципы теории фракталов при территориальном планировании ГА. В России данная теория по отношению к пространственному развитию агломераций практически не применяется (на сегодня опубликованы не более 5 статей по использованию теории фракталов для планирования городов) [3]. В иных науках фракталы применяются учёными России более активно: геология, экология, астрономия и т.п.
В остальном мире фракталы активно используются в городском планировании, например, при анализе пространства городских агломераций, в обосновании их сбалансированного развития в регионе (Франция, Италия, США, Китай, Алжир и т.п.).
Фрактал – это структура, состоящая из частей, которые в каком-то смысле подобны целому. Самоподобие означает, что объект может быть построен на основе любой своей части. Подобие части и целого означает масштабную инвариантность. Легко убедиться, что нет ни одной реальной структуры, которую можно было бы последовательно увеличивать бесконечное число раз и которая выглядела бы при этом неизменной. Тем не менее, принцип самоподобия в приближенном виде имеется в природе: в линиях берегов морей и рек, в очертаниях облаков и деревьев, в турбулентном потоке жидкости и в иерархической организации живых систем, звёздные системы и галактики часто также устроены по принципу фракталов. Самоподобие предполагает наличие некоего инварианта, сохраняющегося при преобразованиях. Наличие инварианта говорит об определенной симметрии самоподобных объектов. О самоподобии говорят нам русские матрешки, теория преформации (предварительное формирование), свойства голограмм [1].
Фракталы как инструмент объяснения и моделирования социально-экономических, пространственных структур применяется сравнительно недавно. Первые упоминания о практическом применении фракталов можно встретить лишь после 1977 года.
Довольно много исследователей отмечают фрактальную природу городов и городских систем [13]. Простейшая схема фрактального города выглядит так (рис. 1, 2, 3)
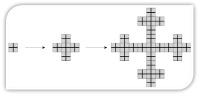
Рис. 1. Образование «Ковра Серпинского». Пример самоподобного образования сложного объекта из простых. Выявляется иерархия морфологии ГА
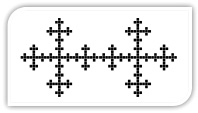
Рис. 2. Срастание «Ковров Серпинского», образование системы более высокого уровня
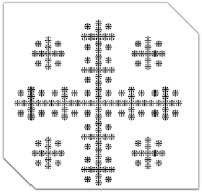
Рис. 3. Фрактальная схема сложных агломерационных скоплений
Выделяется три типа самоподобия: строгое, квази, статистическое. Для городских систем характерно квазифрактальное (или мультифрактальное) и статистическое самоподобие. Форма города или ГА приближённо повторяет саму себя на различных масштабах наблюдения. Особенно это заметно на примере планировки средневековых городов-крепостей с целым рядом круговых оборонительных сооружений (например, Москва).
Планировка современных городов и ГА аналогично имеют повторы на разных масштабах, при этом геометрические формы мультифрактального развития города могут быть разными (рис. 4).
Самая простая форма города: квадрат или круг. При фрактальном планировании происходит перегруппировка частей, когда площадь остаётся неизменной, но увеличивается граница. В результате многократных вариаций на различных масштабах планирования происходит оптимизация расположения инфраструктуры, застройки и зонирования города или ГА.
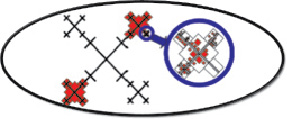
Рис. 4. Квазифрактальное самоподобие на 3-х уровнях в ГА: квартал ядра ГА, ядра ГА, система ГА
Соответственно в городском планировании фракталы используются для [11]:
- Морфологических характеристик городских моделей.
- Преобразования правил планирования в геометрическое русло.
- Моделирования городского роста.
- Избегания фрагментации природных ландшафтов.
- Повышения энергетической автономии в пригородной зоне.
При описании морфологических характеристик городских моделей используется две меры: плотность, фрактальная размерность.
Как измерить фрактальную размерность?
1. Имеем карту города. Разбиваем её на клетки. Часть клеток будут иметь застройку, а часть будут пустыми (площади, дороги, леса, озёра, скверы и т.п.). Размер квадратов в сетке можно варьировать. При гигантском размере квадрата, охватывающем всё пространство города, фрактальная размерность равна 2.
2. Если уменьшить размер квадрата до 20–50 метров, то размерность уменьшится. Уменьшение размера квадрата называется итерацией. При итерации меняется:
- количество подсчитанных элементов – квадратов (N);
- размер исследуемой площади (e).
3. Фрактальную размерность подсчитываем по формуле:
D = log N/log(1/r), (1)
где D – показатель фрактальной размерности; 1/r – понижающий коэффициент (т.е., например, если предыдущая клетка дробится на 16 клеток, то r = 4, если на 9, то r = 3).
За N берём количество застроенных квадратов на анализируемом масштабе, т.е. если застройка имеется в 9 квадратах из 9, то D = 2, если застройка имеется в 4 квадратах из 9, то D = 1,26 и т.д.
4. Далее проводим итерацию и начинаем считать размерность на более мелкой сетке, т.е. идёт поэтапное сокращение размера сетки элементов от крупнозернистого к мелкозернистому.
5. Процедура МУП-анализа позволяет выявить оптимальные площади застройки.
Что такое МУП-город (от англ. MUP-city)? (рис. 5)
Для МУП-анализа выявлены правила оценки актуальности клеток для жилой застройки:
1. Обеспечение доступа к открытым пространствам.
2. Близость к существующим дорогам.
3. Доступность к местам услуг и торговли первого порядка.
4. Доступность к местам услуг и торговли второго порядка.
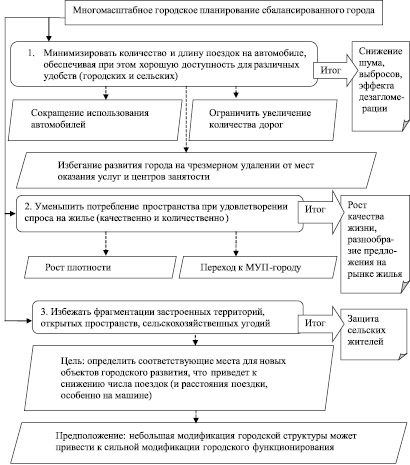
Рис. 5. МУП-анализ
Критерии правил:
1. Число незастроенных клеток вокруг застроенной.
2. Расстояние до ближайшей дороги.
3. Расстояние от оцениваемой клетки до клетки оказания услуг/занятости; диверсификация и количество центров услуг/занятости в каждой группе первого (второго и иных) порядка.
На городском масштабе фрактальное планирование предполагает 3 уровня степени посещаемости центров (ежедневный – кластер 1-го порядка, еженедельный – кластер 2-го порядка, ежемесячный – кластер 3-го порядка). Соответственно при фрактальном моделировании используется различный масштаб клеток: 150–250, 400–600 м, 2–6, 4–10 км радиус. Значит, при рассмотрении трех степеней посещаемости используется выявление ещё кластеров третьего порядка.
Данный подход одновременно учитывает две основные характеристики территориальной структуры города: форма освоения и характер происходящих процессов.
Преимущества территориального планирования с использованием принципов теории фракталов:
1. Возможность обосновать расстояния объектов застройки друг от друга таким образом, что удобство и оптимальность расположения застройки будут сохраняться, а плотность может быть увеличена без ущерба для транспортной доступности.
2. Снижение к минимуму площади используемого городского пространства без увеличения плотности.
3. Организация мультиузорного планирования территории при обеспечении хорошего доступа к различным видам и городских и сельских удобств поможет снизить риск разбросанного хаотичного разрастания. Тем самым снижаются риски ослабления экологии и роста осложнений при организации транспортных потоков.
4. Повышение доступа к центрам услуг и занятости при минимальной пространственной фрагментации.
5. Данный подход позволяет частично побороть эффекты дезэкономии: перегруженность дорог, снижение скорости движения транспортных средств, сужение проезжей части, снижения возможностей для парковки автомобиля.
Фрактальный подход пригоден для устранения разрыва между исследованиями отдельных городов и систем городов [12].
Практическое применение
Фрактальный подход пространственного освоения территории, разработанный французским учёным Франкхаузером, основан на математической теории фракталов, теории Кристаллера и концепции города-сада [9]. Введены новые принципы: новое видение транспортной структуры, рост доступности услуг в модели, приоритет общественного транспорта, доступность зеленых зон на всех масштабах иерархической структуры.
Существуют наработки трёхмерного моделирования фрактального пространства города. Например, для Брюссельской ГА фрактальная размерность застроенной поверхности может отличаться даже при одинаковой плотности застройки. Это изменение может быть объяснено уровнем организации застройки. Средняя плотность застройки дает примерное представление об уровне занятости поверхности, в то время как фрактальная размерность даёт представление об устройстве внутренней структуры застроенных пространств [14]. Фрактальная размерность отличается у одной части города от другой. Фрактальная размерность растёт по мере старения города и увеличения плотности застройки [6].
Фрактальная модель позволяет картографически представить и классифицировать зоны потенциального освоения в ГА [8]. Для городов наиболее характерная размерность : 1,0 ≤ D ≤ 1,8. Сравнение между городами во всем мире приводит к среднему числу D = 1,713.
Со временем размерность города растет. Так, для Лиссабона: D (1960) = 1,42, D (1990) = 1,61 и D (2004) = 1,66.
Выделяется пять фрактальных уровней, для каждого из которых нужен свой подход в развитии [8]:
Тип 1: сельское хозяйство и леса (D ≤ 1,00).
Тип 2: большая доля свободных пространств, освоение – вдоль дорог, иногда образуются небольшие ядра застройки (как маленькие поселения) (1,00 < D≤ 1,26).
Тип 3: рост застройки. Рост городских ядер и образование всё новых ядер (1,26 < D ≤ 1,54).
Тип 4: высокая застройка, но начинается стагнация её роста, что находит отражение в достижении пика прироста размерности (1,54 < D ≤ 1,78).
Тип 5: экономический центр города. Прирост размерности стремится к 0, т.к. возможности новой застройки сильно снижены (1,78 < D ≤ 2,00).
Наиболее эффективно планирование в типах 3 и 4.
Данная методика была использована при территориальном планировании транспортной инфраструктуры Лиссабона в 2005–2008 гг.
Интересно то, что города с похожей структурой освоения территории обладают приблизительно равной размерностью. Так, для американского типа ГА характерен один порядок размерности, а для типа, по которому развиваются Берлин и до недавнего времени Москва – иной.
Фрактальная логика при моделировании систем ГА на региональном уровне отличается от логики городского уровня. Связано это с тем, что в действие вступают уже сформированные системы [1]. Методика фрактального планирования развития ГА не развита.
Результаты исследования: фрактальный подход к агломерациям
Фракталы за рубежом уже применялись для анализа региональной экономики [10]. Фракталы являются фундаментальным инструментом, закладывающим основы для углубленного анализа ГА [10]. Один из немногих отечественных ученых, применяющих фрактальную теорию к ГА, Ю.В. Храмов, выявил зависимость между размерностью и рангом города[5].
Мы предлагаем расширить прикладной аспект фрактальной теории в части использования ее при построении классификации агломерационных систем расселения различных масштабов. Это позволит устранить многозначность толкования определений составляющих агломерационных систем вне зависимости от их масштаба.
Мы утверждаем, что суть процессов, происходящих в агломерациях из трёх деревень и агломерациях из трёх городов-миллионников, практически не отличается. Механизм получения «агломерационной выгоды» один и тот же. Различия лишь в уровне углубления данных процессов (до каких секторов экономики продвинется эффект).
Данное утверждение позволяет рассматривать все системы населенных мест вне зависимости от их масштаба как самоподобные (мультифракталы и статистические фракталы). Отсюда, можно выделить агломерации различных порядков (уровень порядка зависит от рассматриваемого масштаба поселенческой системы). Каждая такая агломерация есть самоподобная структура, являющаяся частью более крупной агломерационной системы, в то же время состоящая из группы агломераций более низкого порядка (таблица).
Иерархия агломерационных систем
|
Уровень системы |
Система |
Составляющие системы |
||
|
Микроуровень: город как агломерация (1-й порядок) |
Тольятти |
Центральный район |
Автозаводской район |
Комсомольский район и др. |
|
Мезоуровень: городская агломерация (2-й порядок) |
Тольяттинская агломерация |
Тольятти (1-й порядок) |
Жигулёвская ГА |
Тимофеевка и др. |
|
Макроуровень: конурбация (3-й порядок) |
Самарско-Тольттинская агломерация |
Самарская агломерация (2-й порядок) |
Тольяттинская агломерация (2-й порядок) |
Сызранская агломерация (2-й порядок) |
|
Региональный/национальный уровень: мегалополис (4-й порядок) |
Мегалополис (Большая Москва) |
Московская ГА (3-й порядок) |
Тверская ГА |
Иные ГА Центра России |
|
Национальный уровень: национальная система расселения – совокупность мегалополисов (5-й порядок) |
Совокупность мегалополисов Москва-Санкт-Петербург |
Большая Москва (4-й порядок) |
Большой Санкт-Петербург (4-й порядок) |
- |
Самарско-Тольяттинская агломерация (Далее – СТА) также является мультифракталом. Её можно рассмотреть в разных масштабах и выявить, что состоит она из ГА разных порядков.
Для примера используем данный принцип рассмотрения ГА при анализе Санкт-Петербургской ГА: Санкт-Петербургский регион расселения (помимо Ленинградской области, простирается на территорию южной части Карелии, всей Новгородской области, северной и срединной частей Псковской области) – внутри него Санкт-Петербургская городская формация – часть территории этой формации занимает Санкт-Петербургская городская агломерация [6].
Дело в том, что данная закономерность при построении многих ГА была замечена довольно давно. Однако адекватной теории, объясняющей факт самоподобия систем расселения в различных масштабах, не существовало до обращения к фрактальной теории.
Важным плюсом применения данной теории к различным по масштабам агломерационным системам является объективность, т.к. она применима ко всем агломерациям вне зависимости от их мощности.
Выводы
Фрактальная теория позволяет подойти к территориальному планированию ГА как к сложному многослойному объекту. Преимущество подхода в том, что он позволяет объяснить (в т.ч. математически) принцип развития систем расселения, опираясь на свойства мультифрактальности. Открываются перспективы формирования математической модели, объясняющей на первый взгляд хаотичную застройку урбанизированных территорий. Внедрение данного подхода позволит ГА развиваться без образования единых урбанизированных массивов.
Рецензенты:
Королева Е.Н., д.э.н., профессор, зам. директора Института Национальной экономики, СГЭУ, руководитель лаборатории комплексных региональных исследований, г. Самара;
Смирнов С.В., д.т.н., профессор, директор ФГБУН «Институт проблем управления сложными системами Российской академии наук», г. Самара.
Работа поступила в редакцию 30.10.2013.
Библиографическая ссылка
Павлов Ю.В. ФРАКТАЛЫ КАК ИНСТРУМЕНТ ТЕРРИТОРИАЛЬНОГО ПЛАНИРОВАНИЯ АГЛОМЕРАЦИОННЫХ СИСТЕМ // Фундаментальные исследования. 2013. № 10-10. С. 2242-2248;URL: https://fundamental-research.ru/ru/article/view?id=32744 (дата обращения: 08.07.2025).



