Пористые материалы широко распространены в природе, в современной технике и промышленности. Значительный интерес представляют исследования волновой динамики и акустики дисперсных сред применительно к проблеме подавления звуковых возмущений пористыми средами.
Первая математическая модель пористой среды, состоящей из твердого тела (скелета), пронизанного длинными узкими каналами (порами), заполненными жидкостью, была изложена в [6]. Однако она была весьма идеализированной и неполной, так как позволяла описать только характер затухания акустической волны и не объясняла другие значимые механические эффекты. Позже были разработаны несколько теоретических и полуэмпирических моделей, которые также имели весьма существенные недостатки. С их помощью не удавалось связать частотные характеристики (инерционные и диссипативные), скорость звука и его затухание с измеряемыми структурными элементами сред и физическими свойствами материалов.
Статья Х.А. Рахматулина «Основы газодинамики взаимопроникающих движений сжимаемых сред» [4] положила начало новому этапу развития механики многофазных сред. В ней объединились достижения, идеи и методы газодинамики, механики взаимопроникающих континуумов и реальных процессов межфазного взаимодействия.
Уравнения многоскоростного движения и тепломассообмена в многофазных средах, а также выражения для внутренних и межфазных взаимодействий в плотноупакованных зернистых, порошкообразных и пористых средах были впоследствии получены Р.И. Нигматулиным на основе пространственного осреднения [2, 3].
Теоретический анализ характеристик акустических волн Био, распространяющихся в пористых средах, применительно к случаям насыщения порового пространства жидкостью и в случае газового заполнения пор, выполнен в работе [1]. Численное исследование дисперсии фазовой скорости и коэффициента поглощения продольных волн проведено на основе теории Био для упругих волновых процессов в двухкомпонентной среде.
В сухой насыщенной газом пористой среде влияние теплообменных процессов на распространение волн исследовано в работе [5]. Указаны области частот, когда затухание волн в насыщенной газом пористой среде определяется в основном теплообменными процессами.
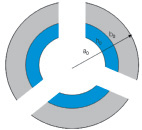
Рис. 1. Ячейка пористой среды
Основные уравнения
При описании распространения одномерных волн во влажной пористой среде примем следующие допущения: значения длин рассматриваемых волн намного больше размеров пор; скорости жидкой пленки и скелета при прохождении волны равны (υl = υs). В качестве характерных размеров среды примем средний радиус пор a0, среднюю толщину водной пленки h0 и среднюю полутолщину стенок пор b0 (рис. 1).
Система уравнений, описывающих рассматриваемый процесс, имеет следующий вид:
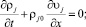
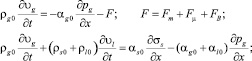
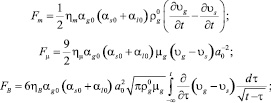(1)
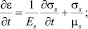
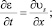
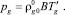
Здесь pg – давление в газовой фазе; αs, αl и αg – объемные содержания твердой, жидкой и газовой фаз соответственно; σs – напряжение в скелете; Fm – сила присоединенных масс, вызванная инерционным взаимодействием фаз; Fμ – аналог силы вязкого трения Стокса; FB – аналог силы Бассэ, проявляющейся при высоких частотах из-за нестационарности вязкого пограничного слоя около границы с твердой фазой; μg – динамическая вязкость газа; ρj,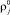 
, υ j, pj, αj – средняя по объему и средняя по фазе плотности, скорость, давление, объемные содержания.
Дополнительным нижним индексом (0) определены параметры, соответствующие невозмущенному состоянию, а параметры без индекса выражают малые возмущения параметров от равновесного значения; верхний индекс (0) соответствует истинному значению параметра.
Для описания неоднородностей температуры произведем схематизацию структуры среды, используя ячеистую схему. При этом пористую среду, насыщенную газом, примем как систему сферических газовых пузырьков, окруженных слоем жидкости и материала скелета. Таким образом, в каждой макроскопической точке, определяемой координатой x, вводим типичную ячейку, состоящую из газового пузырька со слоем жидкости и приходящегося на него скелета. Внутри ячейки имеется распределение микропараметров, а именно температуры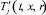 
и плотности газа 
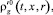где r – микрокоордината, отсчитываемая от центра ячейки. В дальнейшем штрихами наверху снабжены микропараметры.
Для истинных плотностей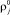 
и объемных содержаний αj справедливы следующие кинематические соотношения:
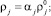
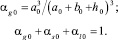
Распределения температур в ячейке пористой среды получим на основе системы уравнений теплопроводности:
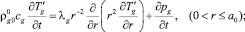
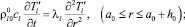(2)
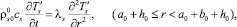
где λj и cj – соответственно коэффициенты теплопроводности и удельной теплоемкости при постоянном давлении (j = g, l, s).
Граничные условия для данной системы имеют вид:
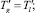
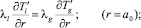
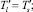
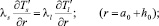(3)
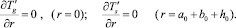
Решение системы уравнений будем искать в виде затухающих бегущих волн:
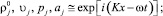(4)
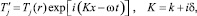
где ω – круговая частота; K – комплексное волновое число; δ – коэффициент затухания.
Из условия существования решения вида (4) получим дисперсионное соотношение, на основе которого можно проанализировать характеристики распространения волн:
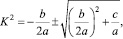
где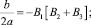 
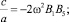
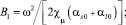
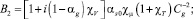
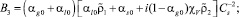
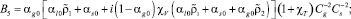
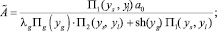
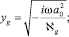
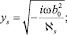
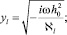
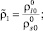
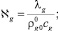
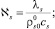
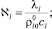
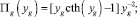
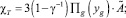
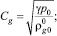
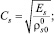
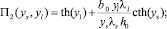
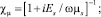
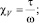
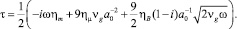
Результаты расчета
В расчетах параметры фаз взяты при температуре среды 300 К. Для воздуха:
γ = 1,4,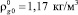 
, cg = 1006 Дж/(кг∙К), λg = 0,027 Дж/(м∙с∙К), μg = 1,86∙10–5 Па∙с.
Для резины:
μs = 108 Па∙с, λs = 0,15 Дж/(м∙с∙К), cs = 1571 Дж/(кг∙К),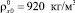 
, Es = 108 Па.
Для воды:
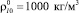, cl = 4200 Дж/(кг∙К), λl = 0,6 Дж/(м∙с∙К).
На рис. 2 показаны зависимости коэффициента затухания δ и фазовой скорости Cp «быстрой» и «медленной» волн от частоты ω для системы «резина – вода – воздух»; характерные размеры среды a0 = 103 м. Линия 1 – жидкая фаза отсутствует, αs0 = 0,2, αg0 = 0,8; линия 2 – αl0 = 0,07, αs0 = 0,13, αg0 = 0,8.
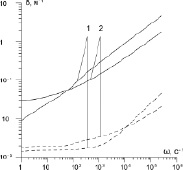
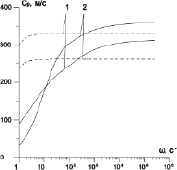
Рис. 2. Влияние водной пленки на коэффициент затухания и фазовую скорость «медленной» (сплошные линии) и «быстрой» (пунктирные линии) волн
Видно, что наличие жидкости приводит к тому, что для «медленной» волны в диапазоне частот ω ≤ 80 с–1, а для «быстрой» волны в диапазоне частот ω ≤ 104 с–1 коэффициент затухания больше, чем в случае «сухой» пористой среды. Это связано с тем, что водная пленка является дополнительным «балластом» для скелета и, таким образом, как бы увеличивает его массовую долю. Также из рис. 2 видно, что скорость «быстрой» волны из-за «утяжеления» скелета водой уменьшается на 68 м/с. Для «медленной» волны при частотах ω ≤ 10 с–1 наличие водной пленки приводит к уменьшению фазовой скорости, а для высоких частот к увеличению (около 47 м/с) скорости звука по сравнению со случаем, когда водной пленки нет.
На рис. 3 представлены зависимости коэффициента затухания и фазовой скорости обеих волн от частоты для разных объемных содержаний газовой фазы при постоянном объемном содержании скелета. Линии 1 – a0 = 10–3 м, b0 = 4,5∙10–5 м, h0 = 2,8∙10–5 м αg0 = 0,8, αs0 = 0,13, αl0 = 0,07, линии 2 – a0 = 10–3 м, b0 = 5,2∙10–5 м, h0 = 9,1∙10–5 м αg0 = 0,67 αs0 = 0,13, αl0 = 0,2.
Видно, что изменение объемного содержания жидкой фазы с 0,07 до 0,2 приводит к росту коэффициента затухания «быстрой» и «медленной» волн. При этом скорость «быстрой» волны уменьшается на 60 м/с, что связано с увеличением доли жидкой фазы в пористой среде. Скорость «медленной» волны при меньшем объемном содержании газовой фазы меньше в диапазоне частот ω ≤ 30 с–1, тогда как в области частот ω > 30 с–1 скорость «медленной» волны постепенно растет, достигая на высоких частотах различия до 33 м/с.
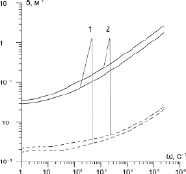
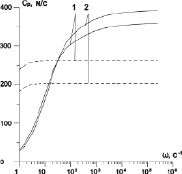
Рис. 3. Влияние объемного содержания газовой фазы на коэффициент затухания и фазовую скорость и «медленной» (сплошные линии) и «быстрой» (пунктирные линии) волн
Стоит отметить, что увеличение объемного содержания скелета приводит к росту скорости «быстрой» волны, что связано с упругими свойствами скелета. Коэффициент затухания «медленной» волны при этом выше во всем диапазоне частот. «Быстрая» волна затухает меньше в случае большего объемного содержания скелета в диапазоне частот ω ≤ ω*, тогда как в области частот ω > ω* картина затухания меняется (здесь ω* – некоторая характерная частота, зависящая от объемного содержания скелета среды).
Выводы
В результате проведенных в работе вычислений установлено, что:
- увеличение объемного содержания водной пленки при постоянном объемном содержании газовой фазы приводит к росту коэффициента затухания и уменьшению скорости «быстрой» волны, что связано с эффектом «утяжеления» скелета водой;
- увеличение объемного содержания скелета при постоянном объемном содержании жидкости приводит к росту скорости «быстрой» волны, что связано с вязко-упругими свойствами скелета;
- уменьшение массовой доли газа и увеличение массовой доли воды приводит к снижению фазовой скорости «быстрой» волны, что связано с ролью жидкости как «утяжелителя» скелета. При этом скорость «медленной» волны уменьшается на низких частотах и увеличивается на высоких частотах.
Рецензенты:
Михайлов П.Н., д.ф-м.н., профессор, заведующий кафедрой алгебры, геометрии и методики обучения математике, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;
Биккулова Н.Н., д.ф-м.н., профессор, заведующий кафедрой общей физики, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Работа поступила в редакцию 30.10.2013.
Библиографическая ссылка
Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. ОБ ЭВОЛЮЦИИ ЗВУКОВЫХ ВОЛН ВО ВЛАЖНЫХ ПОРИСТЫХ СРЕДАХ // Фундаментальные исследования. – 2013. – № 10-10. – С. 2198-2202;URL: https://fundamental-research.ru/ru/article/view?id=32735 (дата обращения: 22.11.2024).