Для расчета и анализа энергетических характеристик процесса резания порубочных остатков дисковой рубительной машиной [1] исследуем дифференциальное уравнение вращательного движения диска с ножами (рис. 1).
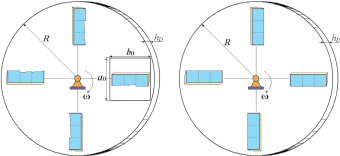
Рис. 1. Расположение на диске режущих элементов с тремя и одним лезвием
Для вывода используем уравнение Лагранжа 2-го рода:
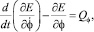(1)
где φ – обобщенная координата, угол поворота диска с ножами;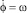 
– обобщенная скорость, угловая скорость диска с ножами; E – кинетическая энергия диска с ножами; Qφ – обобщенная сила, действующая на диск с ножами.
Кинетическая энергия диска с ножами:
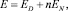(2)
где ED – кинетическая энергия диска; EN – кинетическая энергия ножа; n – количество ножей на диске.
При вращательном движении имеем:
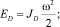
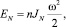(3)
где JD, JN – моменты инерции диска и ножа относительно оси вращения [2].
Приближенно можно записать для моментов инерции диска и ножа:
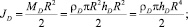
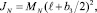(4)
где MD, MN – массы диска и ножа;ρD – плотность материала диска; R, hD – радиус и толщина диска.
Масса комбинированного и традиционного ножа (рис. 2) определится как
MN = ρNGN, MNtr = ρNGNtr,
где GN, GNtr – объемы комбинированного и традиционного ножей; ρN – плотность материала ножа.
Объемы традиционного ножа и комбинированного (рис. 2) вычисляются по формулам геометрии для многогранников.
Масса традиционного ножа:
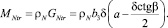(5)
Для комбинированного ножа из трех лезвий общая масса :
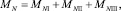
где масса участка I:
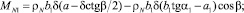
масса участка II:
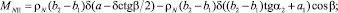
масса участка III:
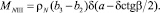
Теперь формулы для момента инерции традиционного и комбинированного ножей запишутся в виде:
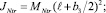
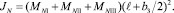(6)
Окончательно кинетическая энергия запишется в виде:
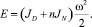(7)
Обобщенная сила складывается из моментов действующих внешних сил относительно оси вращения диска с ножами [3, 4]:
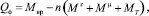(8)
где Mвр = const – момент вращения двигателя привода, раскручивающего диск с ножами; Mz – момент сил сопротивления резанию; Mμ – момент сил вязкого трения; MТ = const – момент силы сухого трения скольжения.
Момент режущих сил пропорционален квадрату угловой скорости вращения диска с ножами:
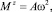(9)
где коэффициент A является функцией геометрических и физических параметров и характеристик ножа.
Момент сил вязкого трения пропорционален первой степени угловой скорости вращения диска с ножами[5, 6]:
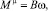(10)
где коэффициент B является функцией геометрических и физических параметров и характеристик ножа.
Момент MT сил сухого трения скольжения не зависит от угловой скорости вращения диска с ножами,следовательно, обобщенная сила примет вид:
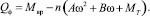(11)
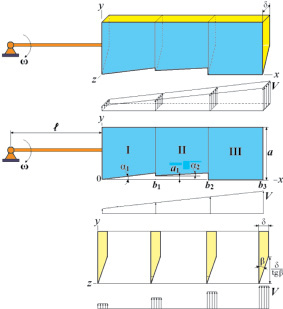
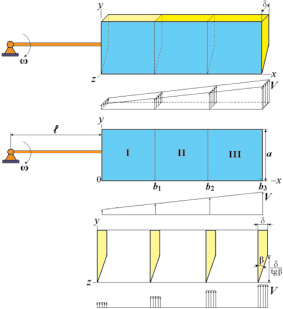
Рис. 2. Общий вид режущего элемента: а – с тремя лезвиями, расположенными ступенчато (комбинированный нож); б – с одним лезвием (традиционный нож)
Вычисляем нужные производные от кинетической энергии в уравнениях Лагранжа 2 рода
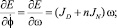
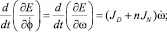
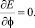
С учетом выражения для обобщенной силы, получим следующее нелинейное обыкновенное дифференциальное уравнение движения диска с ножами:
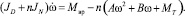(12)
Полученное уравнение (13) описывает динамику вращательного движения диска с n ножами с учетом найденных моментов внешних сил сопротивления и действующего вращательного момента привода.
Исследуем полученное уравнение движения (12) диска с ножами. Для этого представим его в приведенном виде:
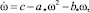(13)
где
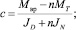
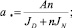
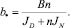
Отсюда, разделяя переменные, получим:
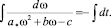
После интегрирования будем иметь:
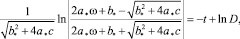
где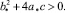 
Знак модуля опустим, поскольку, выбирая угловую скорость ω вращения диска достаточно большой, можно добиться положительности числителя:
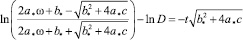
или
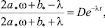
где
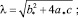
– произвольная постоянная определяется из начальных условий ω(0) = ω0.
Разрешая полученное уравнение относительно ω, получим выражение для угловой скорости вращения, как функции времени [7]:
(14)
За счет значительного вращательного момента Mвр, входящего в коэффициент c, показатель λ экспоненциальной функции достаточно велик и переходные процессы установления угловой скорости вращения диска с ножами весьма быстрые.
При t → ∞ установившееся значение угловой скорости вращения диска с ножами примет вид:
(15)
Это выражение для ω(∞) эквивалентно выражению
(16)
определяющему равенство нулю суммы моментов внешних сил в установившемся процессе резания порубочных остатков.
Полученные моменты режущих сил, сил вязкого и сухого трения и проведенный анализ динамики движения диска с ножами позволяет оценить мощности всех рассмотренных внешних сил.
Мощность внешних сил при вращательном движении тела определяется по формуле:
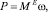
где ME – момент внешних сил относительно оси вращения; ω – угловая скорость вращения.
Применительно к рассматриваемой задаче исследования процесса резания порубочных остатков n ножами, расположенными на вращающемся с угловой скоростью ω диске,формулы для вычисления мощностей принимают следующий вид.
Мощность момента сил сопротивления резанию:
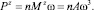(17)
Мощность момента сил вязкого трения:
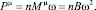(18)
Мощность момента сил сухого трения скольжения:
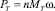(19)
Суммарная мощность сил сопротивления:
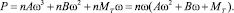(20)
Формулы (17)–(20) позволяют рассчитывать мощности внешних сил как функции параметров движения, геометрических и физических характеристик рассматриваемых ножей.
Мощность сил вращения двигателя привода, раскручивающего диск с ножами равная суммарной мощности сил сопротивления:
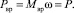(21)
Производительность П, кг/с, процесса резания порубочных остатков может быть оценена как
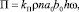(22)
где kП – коэффициент потерь при резании; ρ – плотность сплошной среды порубочных остатков; n – число ножей; a0, b0 – размеры (рис. 1) окна подачи порубочных остатков; h – толщина срезаемого слоя порубочных остатков в рубильной машине; ω – угловая скорость вращения диска с ножами.
Полученные теоретические оценки процесса измельчения древесины ножами различной конструкции полностью подтвердились при использовании построенной модели, а именно: комбинированный нож (рис. 2, а) с заданными параметрами эффективней, чем традиционный нож (рис. 2, б). Суммарный момент всех сил сопротивления резанию, сил вязкого трения и сухого трения скольжения у комбинированного ножа на ≈9,4 % меньше, чем у традиционного ножа при их заданных геометрических характеристиках. При этом «вклад» различных составляющих в такое улучшение характеристик у комбинированного ножа различен:
– уменьшение собственно сил и момента сил сопротивления резанию составило соответственно ≈ 0,4 и 0,2 %.
– уменьшение сил и момента сил вязкого трения составило соответственно ≈ 3,5 и 3,3 %.
– уменьшение сил и момента сил сухого трения скольжения составило соответственно ≈ 4,9 и 5,9 %.
На такое же число процентов улучшились и такие энергетические характеристики (мощности сил сопротивления) в случае применения комбинированного ножа.
Абсолютное значение суммарной мощности сил сопротивления не превысило 67 кВт при принятых исходных данных. Масса комбинированного ножа получилась меньше, чем традиционного ножа на ≈ 6 %. Показатель λ ≈ 0,63 с–1, характеризующий длительность переходных процессов при действующих моментах сил сопротивления, практически не изменился при использовании комбинированного ножа. Производительность процесса резания рассматриваемыми ножами, при принятых исходных данных, составила ≈ 97 кг/с.
Рецензенты:
Маштаков Д.А., д.с.-х.н., доцент, заведующий кафедрой «Лесное хозяйство и лесомелиорация», ФГБОУ ВПО «Саратовский государственный аграрный университет им. Н.И. Вавилова», г. Саратов;
Панкратов В.М., д.т.н., профессор, заместитель директора, Институт проблем точной механики и управления РАН, г. Саратов.
Работа поступила в редакцию 30.10.2013.
Библиографическая ссылка
Фокин С.В., Березников С.В. О ПРОВЕДЕНИИ АВТОМАТИЗИРОВАННОГО АНАЛИЗА ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ПРОЦЕССА РЕЗАНИЯ ДРЕВЕСИНЫ ДИСКОВОЙ РУБИТЕЛЬНОЙ МАШИНОЙ // Фундаментальные исследования. – 2013. – № 10-10. – С. 2182-2187;URL: https://fundamental-research.ru/ru/article/view?id=32732 (дата обращения: 22.11.2024).