Общеизвестно, что значительные разрушения и гибель людей вызывают не только землетрясения, считающиеся основными толчками, но и их афтершоки – сейсмические события, инициированные основным толчком. Прогнозирование афтершоков не менее актуально, чем прогнозирование основных толчков. В отличие от последних, афтершоковая активность является более определенным процессом, который аналогичен процессу образования трещин при хрупком разрушении горной породы. Благодаря успехам механики разрушения и теории случайных процессов в конце XIX и в XX в. были предложены модели афтершоковых процессов, которые впоследствии были апробированы на огромном материале сейсмологических наблюдений. Вместе с тем на сегодняшний день задача прогнозирования афтершоков далека от решения.
В настоящем исследовании предлагается методика прогнозирования афтершоковых процессов в различных диапазонах магнитуд, основанная на использовании закона Гуттенберга-Рихтера и временной модели афтершокового процесса. Фактически при прогнозировании воспроизводится работа центра сейсмологического мониторинга после сильного землетрясения, когда одной из задач является представление прогноза афтершоковой активности на следующие сутки по данным наблюдений за предыдущие дни.
В качестве примера применения методики приводится ретроспективной прогноз афтершоковой активности зоны Рачинского землетрясения за период с 29.04.1991 по 1993 г. (рис. 1).
Использованные данные
Афтершоковая область Рачинского землетрясения хорошо изучена и в плане представляет собой квазиэллипс, главная ось которого имеет длину 100 км и ориентирована вдоль Главного Кавказского хребта, малая ось – 37 км [1] (рис. 1, а). Данные о сейсмичности зоны Рачинского землетрясения за период с 29.04.1991 по 23.09.1993 взяты из каталога [6], который содержит сведения о 956 землетрясениях с M ≥ 2,5 (магнитуда представительности равна 3), произошедших в афтершоковой области основного толчка.
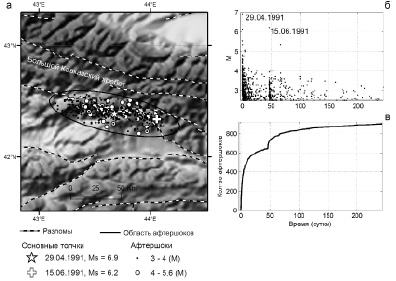
Рис. 1. Основные толчки и афтершоки зоны Рачинского землетрясения за период с 29.04.1991 по 23.09.1993 г. [6] на фоне рельефа и глубинных разломов [5]: а – эпицентры основных толчков и афтершоков с M ≥ 3; б – зависимость магнитуды событий от времени после Рачинского землетрясения; в – зависимость суммарного количества афтершоков от времени
Первый толчок с Ms = 6,9 произошел 29.04.1991 09:12 UT на южном склоне Большого Кавказа (см. рис. 1, а), в Рача-Джавском районе Грузии. В первые сутки после основного толчка интенсивность афтершокового процесса достигала 18 событий с M ≥ 2,5 в час [6].
Через 46,5 суток после этого события 29.04.1991 (15.06.1991 в 0:59 UT), на расстоянии 25 км от него произошло второе Рачинское землетрясение с Ms = 6,2 (см. рис. 1, а), инициировавшее собственный афтершоковый процесс (рис. 1, б, в). К моменту второго Рачинского землетрясения афтершоки первого практически прекратились [2], поэтому эти афтершоковые процессы можно рассматривать независимо.
Использованные модели и методика прогнозирования
К настоящему времени сложилось два подхода к прогнозированию сейсмичности. Первый подход основан на Монте-Карло симуляции афтершокового процесса с заданной условной интенсивностью для генерации возможных сценариев будущей сейсмичности. Второй – на моделировании афтершокового процесса на базисном интервале времени (0, t) и последующем переносе параметров модели на прогнозный интервал (t, t + h). В данной работе мы придерживаемся второго полхода. Достаточно полный обзор методов прогноза приведен в работе [7]. Предлагаемая в настоящей работе методика является развитием подхода, предложенного в работах [3, 4].
Прогнозирование выполнялось с помощью закона Омори-Утсу [11]:
n(t) = K/(t + c)p, (1)
где t – время с момента основного толчка; n(t) – интенсивность афтершокового процесса; K, c, p – параметры модели.
Прогнозирование выполнялось по следующей итерационной схеме. На начальном шаге полагаем t = 1 сутки после основного толчка.
1. Оцениваются параметры закона Омори-Утсу (1) методом максимального правдоподобия по фактическим данным на базисном интервале (0, t).
2. Оценивается количество афтершоков на прогнозном интервале (t, 2t) как интеграл от t до 2t по модели и вычисляется количество афтершоков с магнитудой большей или равной M с помощью подхода Ризенберга-Джонс [10], основанного на использовании закона Гутенберга-Рихтера:
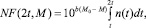 (2)
(2)
где b = 0,83 – параметр закона Гутенберга-Рихтера (LgN = a – bM) для рассматриваемого региона; M0 = 3 – минимальная магнитуда; n(t) – закон Омори-Утсу (1), оцененный на интервале (0, t).
3. Вычисляется прогнозное число афтершоков c магнитудой большей или равной M на интервале (0, 2t) как сумма наблюдаемого числа афтершоков на базисном интервале (0, t) и прогнозного на интервале (t, 2t):
NT(2t, M) = N(t, M) + NF(2t, M), (3)
где NT(2t, M) – прогнозное число афтершоков на интервале (0, 2t) c магнитудой большей или равной M; N(t, M) – наблюденное число афтершоков c магнитудой большей или равной M на интервале (0, t). Если прогнозное число афтершоков на интервале (0, 2t) меньше значения, полученного на предыдущей итерации, NT(2t, M) < NT(2(t – 1), M), то значение с предыдущей итерации принимаем за текущее значение: NT(2t, M) = NT(2(t – 1), M).
4. Увеличиваем длину базисного интервала на одни сутки: t = t + 1, переходим к пункту 1 и начинаем следующую итерацию.
Для оценки качества прогноза используется относительная ошибка:
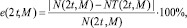 (4)
(4)
где N – фактическое, а NT – прогнозное (3) число афтершоков с магнитудой большей или равной M на интервале (0, 2t).
Помимо закона Омори-Утсу, мы проверяли и другие известные модели афтершоковых процессов, такие как LPL-модель [8] и ETAS-модель [9]. Также тестировалась методика с выбором лучшей модели на каждом шаге с помощью информационного критерия. В результате было установлено, что лучшая (в смысле информационного критерия) модель на базисном интервале (0, t) не означает лучший прогноз на интервал (0, 2t). Лучшие результаты достигаются с использованием закона Омори-Утсу (1), поскольку он имеет меньшее число параметров.
Результаты прогнозирования
Для первого Рачинского землетрясения 29.04.1991 ошибка прогноза афтершоков с M ≥ 3 не превышает 5 % на всем интервале наблюдений; среднее значение ошибки не превышает 2 % (рис. 2). Для сильных афтершоков с M ≥ 4,9 ошибка прогноза достигает 30 % при прогнозировании на 6 сутки по данным за первые 3 суток после основного толчка. Затем ошибка снижается. В дальнейшем значения ошибки не превышают 4 %. Среднее значение ошибки равно 4,5 %.
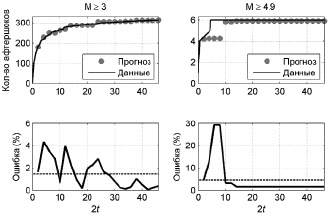
Рис. 2. Прогноз афтершоков первого Рачинского землетрясения 29.04.1991 в различных диапазонах магнитуд по данным за (0, t) на (t, 2t) суток после основного толчка. Пунктиром показано среднее значение относительной ошибки прогноза (4)
Прогноз афтершоков второго Рачинского землетрясения 15.06.1991 (рис. 3). Для M ≥ 3 ошибка прогноза достигает 30 % при прогнозировании на 4 сутки по данным первых 2 суток после основного толчка. Другое пиковое значение ошибки составляет 17 % при прогнозировании на 36 сутки по данным за 18 суток. Затем ошибка уменьшается и далее не превышает 10 % на всем интервале наблюдений. Среднее значение ошибки равно 4.5 %. Для сильных афтершоков с M ≥ 4.2 при прогнозировании на 4 сутки по данным первых двух суток ошибка достигает 80 %; другое пиковое значение ошибки 40 % – прогноз на 38 сутки по данным за 19 суток. Затем ошибка снижается и не превышает 27 %. Среднее значение ошибки прогноза – 27 %.
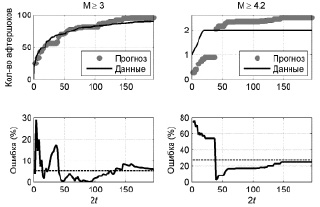
Рис. 3. Прогноз афтершоков второго Рачинского землетрясения 15.06.1991 в различных диапазонах магнитуд по данным за (0, t) на (t, 2t) суток после основного толчка. Пунктиром показано среднее значение относительной ошибки прогноза (4)
Для рассмотренных афтершоковых последовательностей максимальные значения ошибки прогноза приходятся на начало интервала наблюдений. Затем, с течением времени, по мере накопления информации об афтершоковом процессе ошибка снижается.
Заключение
В работе представлена методика прогнозирования афтершоковых процессов в различных диапазонах магнитуд, основанная на использовании закона Гутенберга-Рихтера и временной модели афтершокового процесса. На примере афтершоков зоны Рачинского землетрясения показано, что при использовании в качестве модели закона Омори-Утсу методика дает приемлемые результаты при прогнозировании афтершоков с магнитудами большими или равными магнитуде представительности каталога. При повышении нижнего порога магнитуд для прогнозирования сильных афтершоков качество прогноза ухудшается. Причина заключается во временных вариациях и отклонении параметров закона Гутенберга-Рихтера, оцененных для всего региона, от параметров конкретной афтершоковой последовательности. По-видимому, для улучшения качества прогноза сильных афтершоков следует ввести зависимость от времени в параметры закона Гутенберга-Рихтера и оценивать их на базисном интервале анализируемой афтершоковой последовательности.
Работа выполнена при поддержке гранта РФФИ (проект № 13-05-00158).
Рецензенты:
Скуфьин П.К., д.г.-м.н., ведущий научный сотрудник, ФГБУН «Геологический институт Кольского научного центра Российской академии наук», г. Апатиты;
Олейник А.Г., д.т.н., заместитель директора по науке, ФГБУН «Институт информатики и математического моделирования технологических процессов Кольского научного центра Российской академии наук», г. Апатиты.
Работа поступила в редакцию 08.10.2013.
Библиографическая ссылка
Баранов С.В. МЕТОДИКА ПРОГНОЗИРОВАНИЯ АФТЕРШОКОВЫХ ПРОЦЕССОВ (НА ПРИМЕРЕ ЗОНЫ РАЧИНСКОГО ЗЕМЛЕТРЯСЕНИЯ) // Фундаментальные исследования. 2013. № 10-7. С. 1441-1445;URL: https://fundamental-research.ru/ru/article/view?id=32602 (дата обращения: 12.07.2025).



