При проектировании защитно-диагностических систем, основанных на анализе составляющих поля в торцевой зоне синхронного генератора (СГ) [1-5], необходимы данные с конкретной точки торцевой зоны. Величина воздушного зазора δ, особенно мощных СГ в сравнении с размерами торцевой зоны, значительна. Так, например, в СГ ТВВ-500-2ЕУ3 она составляет 95 мм при высоте и ширине расчетного призматического канала торцевой зоны 1020 и 1193 мм соответственно. При этом максимальное значение индукции магнитного поля воздушного зазора может достигать величины 1,6…2,0 Тл [7]. Поэтому поле «выпучивания» [8] из воздушного зазора в торцевую зону должно быть значительно. Поэтому при расчетах магнитного поля в торцевой зоне СГ необходима оценка влияния поля «выпучивания» из воздушного зазора на выходные параметры измерительного преобразователя.
Цель работы – изложение результатов исследования по моделированию влияния поля «выпучивания» из воздушного зазора на показания точечного преобразователя магнитного поля в торцевой зоне СГ.
Постановка задачи. Разработать простую методику позволяющую учесть магнитное поле «выпучивания» из воздушного зазора при расчете ЭДС на выходе точечного преобразователя магнитного поля, устанавливаемого в торцевой зоне СГ.
Методика моделирования. Точное моделирование поля воздушного зазора является достаточно сложной задачей [9] по целому ряду причин, в частности, из-за неравномерности воздушного зазора в аксиальном направлении у торцов сердечника статора неявнополюсных СГ, а также его неравномерностью в тангенциальном направлении у явнополюсных СГ. Поэтому для его приближенной оценки предлагается воспользоваться моделью, прототип которой изложен в [10, 11]. Эта модель проста и дает неплохие результаты. Основная идея состоит в том, чтобы заменить поле «выпучивания» воздушного зазора полем проводника диаметром dδ = (0,1…0,2)δ с током Iδ в нем. Расчетная схема для моделирования приведена на рисунке, а. Величина тока Iδ в проводнике рассчитываются по уравнению Био–Савара–Лапласа с учетом
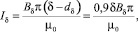
где Bδ – индукция магнитного поля воздушного зазора.
Для определения радиальной и аксиальной составляющей индукции By Bz от проводника с током можно воспользоваться любым метом расчета магнитного поля, но в рамках поставленной задачи наиболее эффективным является усовершенствованный метод зеркальных отражений, в котором предлагается ввести коррекцию токов [12].
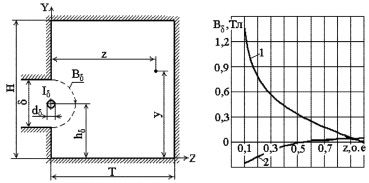
а б
Расчетная схема и результаты расчета поля воздушного зазора в торцевой зоне СГ
Расчет поля проводника с током, расположенного между параллельными ферромагнитными поверхностями, учитывается бесконечным числом отражений [12]. По закону Био–Савара–Лапласа для i, j-гo отражения проводника с током Ix(i,j) вдоль осей y и x соответственно индукция магнитного поля в плоскости, перпендикулярной проводнику, определяется выражением:
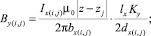
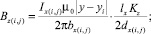
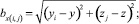
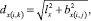
где yi, zj – координаты i, j-гo отражения проводника; μ0 – относительная магнитная проницаемость; y, z – координаты точки, в которой определяются аксиальная – Bz(i,j) и радиальная – By(i,j) составляющие индукции магнитного поля отражений; lx – длина проводника, вдоль которого и разворачивается машина; Ky, Kz – коэффициенты коррекции; bx – расстояние от точки расчета индукции до центра проводника; dx – расстояние от точки расчета индукции до конца проводника.
Если принять, что магнитная проницаемость ферромагнитных элементов равна бесконечности, то величина тока для любого отражения
Ix(i,j) = Ix.
Если магнитная проницаемость не равна бесконечности, то величина тока для i, j-гo отражения равна
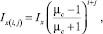
где µс – магнитная проницаемость ферромагнитных элементов.
При расчете Bz в областях 0 < y < hδ и hδ < y < H рис. 1 коэффициент коррекции определяется как
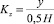и 
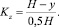
Если в системе координат ферромагнитные поверхности параллельны оси z, то для расчета составляющей индукции магнитного поля By в области 0 < z < Т коэффициент коррекции
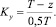
В реальных условиях [9] магнитная проницаемость ферромагнитных стенок в электрических машинах имеет конечную величину и колеблется в пределах 40…1400. В этом случае при расчете Bz в областях 0 < y < hδ и hδ < y < H следует применять коэффициенты коррекции, рассчитанные следующими уравнениями:
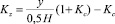
и
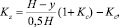
где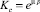 
, а p ≈ –0,00264.
Расчет составляющей индукции магнитного поля By в области 0 < z < Т соответственно осуществляется с коэффициентами коррекции
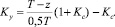
В результате радиальная и аксиальная составляющие магнитного поля от проводника с током Iδ в торцевой зоне определятся как
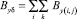
и
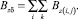
Проверка. Результаты моделирования магнитных полей «выпучивания» воздушного зазора приведены на рис. 1, б, где кривые 1 и 2 радиальная и аксиальная составляющие этого поля при y = hδ. Полученные результаты хорошо согласуются с результатами в [9, 10, 13, 14]. При расчетах в разных частях торцевой зоны расхождение с результатами расчетов, полученных численными методами расчета аксиальной составляющей вблизи торцевого щита, редко достигало уровня 15 %, что вполне удовлетворяет предъявляемых к методике расчета требованиям.
Выводы
Метод зеркальных отражений с коррекцией токов позволяет учесть влияние магнитного поля «выпучивания» на поле в заданной точке торцевой зоны генератора с погрешностью порядка 15 %. Использование при расчете поля простых аналитических выражений дает возможность производить учет влияния магнитного поля «выпучивания» на показания датчиков без дополнительных временных потерь на ПЭВМ.
Работа выполнена в рамках исполнения Госзадания «Наука» ГК № 7.2826.2011.
Рецензенты:
Лукутин Б.В., д.т.н., профессор кафедры ЭПП ЭНИН, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Исаев Ю.Н., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Работа поступила в редакцию 08.10.2013.
Библиографическая ссылка
Полищук В.И., Лиясова О.В., Оболтина А.В. МЕТОДИКА МОДЕЛИРОВАНИЯ ВЛИЯНИЯ ВОЗДУШНОГО ЗАЗОРА НА МАГНИТНОЕ ПОЛЕ В ТОРЦЕВОЙ ЗОНЕ СИНХРОННОГО ГЕНЕРАТОРА // Фундаментальные исследования. – 2013. – № 10-6. – С. 1234-1237;URL: https://fundamental-research.ru/ru/article/view?id=32522 (дата обращения: 18.04.2024).