Проблема рационального использования существующих транспортных сетей населенных пунктов, а также планировка транспортных сетей в новых микрорайонах бесспорно актуальна в настоящее время. Существует большое количество макро- и микромоделей распределения транспортных потоков. Задачи макромоделирования базируются на поиске равновесного распределения потоков, микромоделирование решает проблемы пропускных способностей локальных участков сетей. Из-за различного характера гипотез, закладываемых в макро- и микромодели, задача обмена информацией между ними не решена ни теоретически, ни в виде программных продуктов. Сложность численного решения задачи потокового равновесия в основном зависит от аналитического задания функции транспортных затрат.
Актуальной является задача создания модели функционирования сети, позволяющей на основании минимального количества исходных данных делать адекватные прогнозы эффективности распределения сетевых потоков. Перспективной задачей является разработка микромодели транспортной динамики в узлах сети и оценка их влияния на распределение потоков по сети. Удельные затраты на прохождение конкретной дуги зависят и от потоков по другим дугам.
Граф-представление транспортной сети
Конкретизируем основные понятия, используемые в данной работе. Назовем сетевые потоки неконфликтными, если на данном участке сети они не пересекаются, и конфликтными – в противном случае. Вершинами графа будем считать узловые точки – точки, в которых либо расположены источники или потребители информации, либо происходит пересечение конфликтных потоков. То есть узловые точки образуются пересечением многоканальных магистралей.
В работах [2, 4, 5] автор предлагает следующую классификацию узловых точек (УТ). Пусть одна часть потоков (назовем их главными) проходит через УТ беспрепятственно. Требования второй части потоков (второстепенных) ожидают возникновения достаточных интервалов по времени между требованиями главных потоков для пересечения УТ. Такая УТ названа узловой точкой первого типа.
Рассмотрим теперь узловую точку, в которой для возможности ее пересечения поочередно перекрывается движение для одной из групп неконфликтных потоков на фиксированное время. Это узловая точка второго типа.
Будем придерживаться традиционного представления сети в виде графа. Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое число. Поток на графе – это совокупность однородных объектов (требований), пересылаемых из одной вершины в другую. Таким образом, поток – это некоторая функция, заданная на дугах графа. В разработанной автором модели поток на графе задается в виде функции плотности распределения интервалов по времени между следующими подряд требованиями.
Определение функции транспортных затрат для узловой точки второго типа
В работах [2, 4] подробно рассмотрены методы расчета функции транспортных затрат в случае справедливости гипотезы о распределении интервалов по времени между требованиями по закону Эрланга порядка k, k Î {1, 2, 3, 4}. Справедливость гипотезы и адекватность аналитических моделей подтверждено серией экспериментов. Согласно мнению ряда ученых [1, 3], занимающихся теорией случайных процессов, с помощью обобщенного распределения Эрланга можно аппроксимировать практически любое распределение при правильном подборе параметров. В данной работе рассмотрим функцию транспортных затрат для узловой точки второго типа при справедливости гипотезы об обобщенном распределении Эрланга.
Найдем среднее значение величины Nt – числа требований, прибывающих к данной точке дороги за интервал времени (0; t). H(t) = M(Nt) – функция восстановления (математическое ожидание числа прибывающих за время t требований).
Функция распределения обобщенного закона Эрланга имеет вид:
 (1)
(1)
где 
Преобразование Лапласа f(*)(s) функции плотности распределения f(t) (причем, даже в случае совпадения некоторых из параметров λi):
 (2)
(2)
Тогда преобразование функции простого процесса восстановления [3] имеет вид:
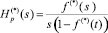 (3)
(3)
Следовательно, H*(s) представляет собой рациональную дробь и может быть разложена на простые дроби. С этой целью необходимо найти корни знаменателя дроби
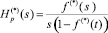 :
:
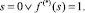 (4)
(4)
Таким образом, разложение H*(s) на простые дроби содержит члены:
1) от полюса s = 0;
2) от ненулевых полюсов в точках, являющихся корнями уравнения f*(s) = 1. Причем это уравнение кроме действительных может иметь только попарно сопряженные комплексные корни, действительная часть которых Re < s.
При k = 1 получим хорошо изученное показательное распределение. Рассмотрим вид функции H*(s) в случае обобщенного закона Эрланга порядков k ∈ {1, 2, 3, 4}.
I случай) k = 2.
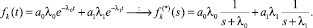
Здесь

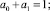
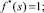
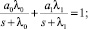
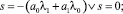
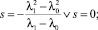
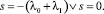
II cлучай) k = 3.
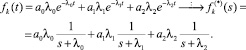
Здесь
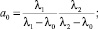
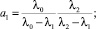
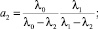

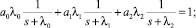
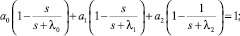
Левая часть последнего уравнения представляет собой многочлен второй степени, нахождение корней которого не вызывает затруднений.
III cлучай) k = 4.
Здесь
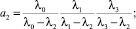
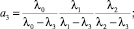
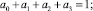
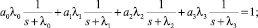
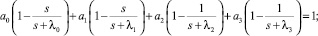
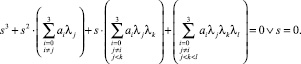
Левая часть последнего уравнения представляет собой многочлен третьей степени, корни которого могут быть найдены с помощью формулы Кардано.
Таким образом, изображение функции восстановления имеет вид:
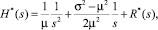 (5)
(5)
где μM(T); σ2 = D(T); R*(s) – сумма простейших рациональных дробей. Следовательно, сама функция восстановления в случае обобщенного закона Эрланга имеет вид:
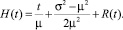 (6)
(6)
Каждому простому действительному корню sp соответствует дробь 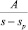 (слагаемое в R*(s)), а ей, в свою очередь, соответствует оригинал
(слагаемое в R*(s)), а ей, в свою очередь, соответствует оригинал 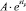 (слагаемое в R(t)).
(слагаемое в R(t)).
Действительному корню sp кратности 2 соответствует в разложении сумма 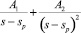 (слагаемые в R*(s)). Следовательно, оригинал имеет вид:
(слагаемые в R*(s)). Следовательно, оригинал имеет вид: 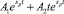 (слагаемые в R(t)).
(слагаемые в R(t)).
Каждой паре комплексно-сопряженных корней 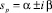 соответствует дробь в разложении
соответствует дробь в разложении 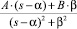 (слагаемые в R*(s)). В этом случае оригинал имеет вид:
(слагаемые в R*(s)). В этом случае оригинал имеет вид: 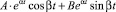 (слагаемые в R(t)).
(слагаемые в R(t)).
Введем ряд обозначений, принятых автором при разработке математической модели функционирования сети. Дуга представляет собой часть многоканальной магистрали, заключенную между двумя вершинами (узловыми точками). Обозначим {lj} – множество дуг графа, {zj} – множество вершин (узловых точек). Для определения показателей эффективности распределения потоков по сети и решения оптимизационных задач введем следующие понятия:
1) ωM(zn) – средняя задержка в узловой точке zn требования выбранного направления;
2) 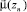 – вес вершины zn (узловой точки) для потока данного направления, то есть средняя суммарная задержка всех требований потока данного направления в узловой точке zn в единицу времени;
– вес вершины zn (узловой точки) для потока данного направления, то есть средняя суммарная задержка всех требований потока данного направления в узловой точке zn в единицу времени;
3) μ(zn) – вес вершины zn (узловой точки), то есть средняя суммарная задержка всех требований в узловой точке zn в единицу времени.
Под задержкой в УТ второго типа будем понимать время простоя в случае, если движение в данном направлении запрещено.
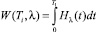 (треб.∙с.) – суммарная задержка требований рассматриваемого потока за Тi секунд – время, в течение которого запрещено движение в рассматриваемом направлении. Простое аналитическое задание функции H(t) в случае обобщенного распределения Эрланга позволяет элементарно получить значение функции W(Ti, λ).
(треб.∙с.) – суммарная задержка требований рассматриваемого потока за Тi секунд – время, в течение которого запрещено движение в рассматриваемом направлении. Простое аналитическое задание функции H(t) в случае обобщенного распределения Эрланга позволяет элементарно получить значение функции W(Ti, λ).
Суммарная задержка всех требований данного потока за единицу времени – один час, выражается следующим образом :
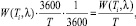 (треб.∙ч.), (7)
(треб.∙ч.), (7)
где 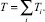
Уточним параметры качества распределения потоков для узловой точки II типа, которые представляют собой функции транспортных затрат в узловых точках сети:
1) 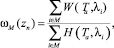 где М – множество выбранных направлений, a ∈ {1; 2};
где М – множество выбранных направлений, a ∈ {1; 2};
2) 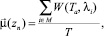 где М – множество выбранных направлений, a ∈ {1; 2};
где М – множество выбранных направлений, a ∈ {1; 2};
3) 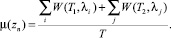
Заключение
Результаты исследования, изложенные выше, являются обобщением проведенной автором работы по оптимизации распределения транспортных потоков по сети. Гипотеза о распределении интервалов по времени между требованиями по закону Эрланга позволила разработать математическую модель, дающую удовлетворительные по точности результаты оценивания качества функционирования сети. Кроме того, минимальный набор исходных параметров сделал менее дорогостоящей разработку базы данных для проведения оценки качества реорганизаций внутри сети. Обобщенный закон Эрланга при правильном подборе параметров позволит с достаточной точностью аппроксимировать практически любое распределение, а следовательно, позволит увеличить рамки применимости модели на потоки более высокой плотности при прохождении ими ряда узловых точек. Это в свою очередь дает возможность увеличить точность при решении оптимизационных задач в теории транспортных потоков.
Работа выполнена при поддержке РФФИ, проект р-юг-а-13-08-96502.
Рецензенты:
Атрощенко В.А., д.т.н., профессор, декан факультета компьютерных технологий, ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар;
Видовский Л.А., д.т.н., профессор, заведующий кафедрой вычислительной техники и автоматизированных систем управления, ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.
Работа поступила в редакцию 11.07.2013.
Библиографическая ссылка
Наумова Н.А. МЕТОД ОПРЕДЕЛЕНИЯ ФУНКЦИИ ТРАНСПОРТНЫХ ЗАТРАТ В УЗЛОВЫХ ТОЧКАХ СЕТИ // Фундаментальные исследования. 2013. № 8-4. С. 853-857;URL: https://fundamental-research.ru/ru/article/view?id=32009 (дата обращения: 18.11.2025).



