Успешное выполнение многих экономических задач полностью зависит от эффективного использования ресурсов предприятия (оборудования, рабочей силы, денег, товаров, сырья, и др.). Именно эффективное использование и ограничения этих ресурсов будет определять итоговый результат его деятельности.
Экономическая сущность методов оптимизации заключается в том, что, имея в наличии определенные ресурсы, выбирается определенный способ их распределения (использования), обеспечивающий максимум (или минимум) интересующего ЛПР (лица принимающего решение) показателя [3].
Трудности, которые могут возникать при решении задач математического программирования:
1) вид функциональной зависимости критерия эффективности, который также называется целевой функцией, от независимых переменных;
2) размерность задачи, а именно количество независимых переменных;
3) вид и количество ограничений, удовлетворяющих независимым переменным.
Современные информационные технологии по оптимизации решений могут применяться для большого круга практических задач, которые включают формулировку (построение) математической модели, а также математические методы и программное обеспечение для решения таких задач, методы математического анализа оптимальности решений.
Оптимизационными задачами нелинейного программирования являются математические модели, которые содержат нелинейные зависимости от переменных.
Решение задач нелинейного программирования по сложности сильно превосходит решение задач линейной модели. Из-за этого долгое время на практике экономического управления линейные модели оптимизации весьма успешно использовались даже в случае нелинейности. В одних ситуациях такая нелинейность не сильно выделялась и ею пренебрегали, а в других – проводилась линеаризация соотношений, обладающих нелинейностью, или применялись такие специальные приемы, как, например, построение аппроксимационных моделей, благодаря чему могли достигаться необходимые требования. Тем не менее весьма часто встречаются такие задачи, нелинейность для которых является существенной, и эти методы аппроксимации будут неэффективны, поэтому нелинейность нужно учитывать в явном виде [3].
В отличие от линейного моделирования не существует какого-либо одного или нескольких алгоритмов, которые будут эффективны для решения каких-либо нелинейных задач. Один алгоритм может быть эффективен для решения задачи определенного вида, но совсем неприемлем для задачи другого вида. В связи с этим существуют алгоритмы для решения каждого типа задач. Важно отметить, что даже компьютерные программы, которые ориентированы на решение определенного вида задач, не будут гарантировать правильность решения каких-либо задач такого типа, и правильность оптимальности решения необходимо проверять в каждом конкретном случае [5].
Задачу с нелинейной моделью оптимизации в общем виде можно представить в отыскании следующего вектора неизвестных переменных (1):
X = (x1, x2, ..., xn), (1)
который позволял бы обращать в максимум (минимум) функцию (2):
Z = f(x1, x2, ..., xn) (2)
и удовлетворял бы следующей системе ограничений (3):
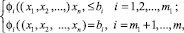 (3)
(3)
где на некоторые из них или на все переменные накладывается условие не отрицательности.
Определение оптимального портфеля инвестиций – важная и весьма распространенная финансовая задача, которую можно решать в сфере страхования, банковского дела, инвестирования и т.д., где идет речь о поиске оптимального варианта распределения некоторой суммы денег на отдельные части [3].
С появлением компьютеров и развитием средств связи начинают появляться новые информационные технологии и новые терминологии, которые входят в нашу повседневную рабочую и личную жизнь. В последние несколько лет все большую популярность приобретают облачные вычисления [7].
Ключевым моментом для возможности предоставления облачных сервисов широкому спектру устройств является создание двусторонней информированности между облаком и клиентом. Очевидно, что с одной стороны не все клиентские устройства имеют одинаковые возможности, с другой – облако в разных ситуациях имеет разную доступность для клиентских устройств. Поэтому единая модель предоставления сервисов не может быть эффективной [1]. Несоответствие между способом доставки сервиса и возможностями устройства может негативно повлиять на производительность труда сотрудников, функциональность и безопасность системы, лишить смысла инвестиции, сделанные для развития облачных сервисов [8, 2].
Рассмотрим случай, когда инвестор хочет вложить определенную сумму денег в некоторое количество облачных ИТ-сервисов (ИТ) и хочет определить, какую именно часть из этой суммы лучше всего вложить в каждый вид сервиса. Выбранный ИТ-сервис будет носить название «инвестиционный портфель».
В задаче данного типа можно применить метод оптимизации – нелинейное программирование. Возможны следующие альтернативные варианты [3, 5]:
1) минимизация риска с ограничением на доход;
2) максимизация дохода с ограничением на риск.
Набор частей суммы инвестирования в инвестиционном менеджменте называется портфелем (portfolio). Оптимальный портфель – это такой набор, в который инвестор включает то, что считает для себя лучшим с учетом доходности вложений и возможным риском потерь [6].
Доходом, который мы получим за определенный период времени от вложения инвестиций, выросший за этот период до некой величины, будет число (положительное или отрицательное), которое вычисляется по следующей формуле:
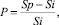 (4)
(4)
где Р – доход; Sp – сумма, полученная за определенный период; Si – инвестированная сумма.
Значение риска в практике инвестирования находится методом измерения величины возможного разброса дохода инвестиционного портфеля от его среднего значения. Такой разброс в статистике носит название вариации или дисперсии. Он находится по формуле (1):
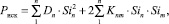 (5)
(5)
где Dn – дисперсия n-го облачного ИТ-сервиса; Sin,m – сумма инвестиции в n-й облачный сервис; Knm – ковариация облачного ИТ-сервиса.
Статистические данные доходов от применения облачных ИТ-сервисов
|
Месяцы |
Доход |
||
|
ИТ-сервис 1 |
ИТ-сервис 2 |
ИТ-сервис 3 |
|
|
1 |
3,0 % |
2,5 % |
4,9 % |
|
2 |
1,3 % |
2,0 % |
2,0 % |
|
3 |
2,6 % |
2,6 % |
1,9 % |
|
4 |
–1,6 % |
–2,2 % |
–2,8 % |
|
5 |
–2,1 % |
1,4 % |
6,9 % |
|
6 |
3,6 % |
1,7 % |
–3,5 % |
|
7 |
3,8 % |
3,1 % |
1,3 % |
|
8 |
8,9 % |
3,5 % |
7,2 % |
|
9 |
9,0 % |
9,5 % |
2,1 % |
|
10 |
8,3 % |
9,0 % |
1,1 % |
|
11 |
3,5 % |
–2,2 % |
0,6 % |
|
12 |
1,6 % |
7,5 % |
90,8 % |
Начальные данные для нашей задачи содержатся в таблице по статистике доходов для всех предполагаемых для использования облачных ИТ-сервисов, собранной за год. Из этой таблицы можно получить следующее:
1. Среднее значение от дохода применяемого ИТ-сервиса.
2. Дисперсию (вариацию) от дохода определенного ИТ-сервиса;
3. Ковариацию от дохода определенного ИТ-сервиса. Это число, которое будет характеризовать зависимость дохода от двух облачных ИТ-сервисов, которые определенным образом связаны между собой, а также влияют друг на друга.
Один из вариантов решения данной задачи – это использовать модель Шарпа, т.е. при заданной статистике доходов находим среднее значение доходов, их дисперсии и ковариации.
Рассмотрим задачу построения нелинейной модели оптимизации, основанной на модели Шарпа, с учетом минимального риска.
Постановка задачи. Инвестирования касаются три вида облачных ИТ-сервиса, для которых известна доходность только за 12 месяцев, а статистические данные (дисперсия и ковариация), которые являются оценками риска, необходимо найти с приведенной статистики доходности ИТ, а затем определить те значения оптимального портфеля, которые обеспечат минимум риска. При этом зафиксируем ограничения: на величину дохода в значении 5 % и на величину первого облачного ИТ-сервиса, чтобы было не больше чем 50 % от общей суммы.
Составим экономико-математическую модель (4) оптимального распределения инвестиций в облачные технологии (ИТ-сервисы).
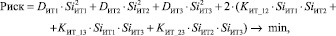 (6)
(6)
при ограничениях:
1) сумма частей портфеля = 100 %;
2) вложения в облачный ИТ-сервис 1 ≤ 50 %;
3) сумма дохода = 5 %;
4) все неизвестные ≥ 0.
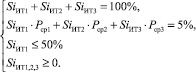
Вычисляем средний доход с помощью функции Excel СРЗНАЧ, дисперсию с помощью функции ДИСПР и ковариацию с помощью КОВАР. Получив значения дисперсии для трех видов облачных ИТ-сервисов и ковариаций, можно вычислить риск, т.е. значение целевой функции.
При помощи сервиса «Поиск решения» в программе Excel находим инвестиционный портфель и значение риска. Для этого устанавливаем целевую ячейку, изменяемые ячейки, вводим ограничения в соответствующие адреса ячеек. Результат решения приведен на рисунке.
Результат вычисления показал, что с учетом риска, равного 0,51 %, распределение инвестиций будет следующим: на ИТ-сервис № 1 пойдет 50 % инвестирования, на ИТ-сервис № 2 пойдет 23,21 %, на ИТ-сервис № 3 – 26,79 %. Отчет по устойчивости определяет теневые цены ограничений в виде множителя Лагранжа.
Заключение
Исходя из всего изложенного, можно сформулировать основные выводы, на которых построен смысл оптимальности распределения портфеля инвестиций в облачные ИТ-сервисы:
1) рынок имеет в своем составе некоторое число активов, доходности каждого из которых для определенного периода являются случайными величинами [4];
2) инвестор может, например, исходя из полученных статистических данных, оценить ожидаемые (средние) значения доходности и их попарные ковариации, и степени ожидаемой диверсификации риска;
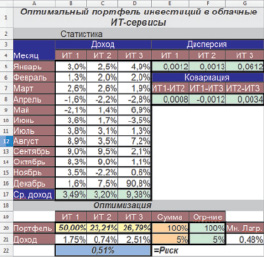
Результат решения
3) инвестор в состоянии сформировать любые возможные (для этой модели) портфели из имеющихся активов на рынке. Доходность от этих портфелей будет также являться случайной величиной;
4) сравнение выбранных портфелей будет основываться только на 2 критериях: риске и средней доходности;
5) инвестор не будет склоняться к риску: из двух возможных портфелей с одинаковой или схожей доходностью он обязательно остановится на портфеле с меньшим риском.
Рецензенты:
Мицель А.А., д.т.н., профессор кафедры автоматизированных систем управления, Томский государственный университет систем управления и радиоэлектроники, г. Томск;
Сапожков С.Б., д.т.н., профессор кафедры механики и инженерной графики, Юргинский технологический институт (филиал) Национального исследовательского Томского политехнического университета, г. Юрга.
Работа поступила в редакцию 01.07.2013.
Библиографическая ссылка
Разумников С.В. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНОЙ МОДЕЛИ ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ ИНВЕСТИЦИЙ В ОБЛАЧНЫЕ ИТ-СЕРВИСЫ // Фундаментальные исследования. 2013. № 8-2. С. 302-305;URL: https://fundamental-research.ru/ru/article/view?id=31913 (дата обращения: 16.07.2025).



