Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бадамшин И.Х. 1

---

1 ФГБОУ ВПО «Уфимский государственный авиационный технический университет»

Наличие массивного вращающегося ротора является особенностью авиационного газотурбинного двигателя (ГТД). Это становится причиной возникновения дополнительных внешних и внутренних нагрузок на двигатель. В настоящей работе на основе разработанной модели центростремительного ускорения рассчитываются внутренние силы, действующие на вращающийся ротор ГТД. Решается первая задача механики. Разработанная модель центростремительного ускорения используется также для объектов с наноразмерами на основе вихревой модели элементарных частиц и атомов. В приведённых примерах подтверждается адекватность модели (а также единство физических законов в природе) на основе примерного равенства сил взаимодействия, определяемых по разным законам. Разработанная модель объединяет четыре взаимодействия в одно. Частными следствиями модели являются объяснения физической сущности некоторых механических явлений, которые имеют лишь математическую трактовку. Например, гироскопический эффект и объяснение самоцентрирования ротора при превышении его критической угловой скорости вращения.

Статья в формате PDF

489 KB

инерционные нагрузки

сила тяжести

ротор ГТД

прочность

фундаментальные взаимодействия

1. Конструкция и проектирование авиационных газотурбинных двигателей / С.А. Вьюнов, Ю.И. Гусев, А.В. Карпов и др.; под общ. ред. Д.В. Хронина. – М.: Машиностроение, 1989. – 568 с.

2. Бадамшин И.Х. Влияние эволюций летательного аппарата на усилия, действующие в ГТД // Фундаментальные исследования. – 2013. – № 6 (2). – С. 251–257.

3. Бадамшин И. Х. Моделирование сил, действующих на газотурбинный двигатель / И.Х. Бадамшин // Вестник УГАТУ.– Уфа, 2011. – Т 15, № 3.-С. 28–32.

4. Бадамшин И. Х. Моделирование упругих характеристик нанокомпозитов и нанотрубок // Композиты и наноструктуры. – М., 2011. – № 1. – С. 18–23.

5. Бадамшин И.Х. Расчёт предела упругости бездефектных монокристаллов в составе эвтектических композитов // Вестник КГТУ им. А.Н. Туполева. – Казань, 2011. – № 4(64). – С. 39–44.

6. Бадамшин И.Х. Модель упругого взаимодействия в прочностных задачах двигателестроения // Молодёжный Вестник УГАТУ. – Уфа, 2012. – № 1(2). – С. 51–54.

7. Бадамшин И.Х. Теоретическая оценка влияния температуры на период кристаллической решётки монокристаллов турбин авиационных ГТД // Вестник СГАУ. – Самара, 2012. – № 1(32). – С. 71–76.

8. Коровин Н.В. Общая химия: учеб. для технических направ. и спец. вузов. – М.: Высш. шк., 1998. – 559 с.

9. Свойства элементов. В двух частях. Ч.1. Физические свойства: Справочник. – 2-е изд. – М.: Металлургия, 1976. – 600 с.

10. Трофимова Т.И. Курс физики: учеб. пособие для вузов. – М.: Высш. шк., 2003. – 542 с.

Наличие массивного вращающегося ротора является особенностью авиационного газотурбинного двигателя (ГТД). Это становится причиной возникновения дополнительных внешних нагрузок на двигатель, в частности, гироскопического момента, возникающего при эволюциях летательного аппарата (рис. 1) [1].

На ГТД также действуют инерционные нагрузки и сила тяжести. В работе [2] обоснована модель расчёта внешних сил, действующих на вращающийся ротор ГТД при эволюциях летательного аппарата. В настоящей работе, пользуясь названной моделью, рассчитываются внутренние силы, действующие на вращающийся ротор ГТД.

Модель и сравнительный анализ

Решается первая задача механики: для заданной траектории движения исследуемого объекта определяются действующие силы. Если вращающееся тело (в частности, ротор) движется по криволинейной траектории, то сила, вызывающая такое движение, является центростремительной. При этом центростремительное ускорение aцс определяется по формуле [2,3]

aцс = (0,5(Vорб + 2Vвр))2/2D, (1)

где Vорб, Vвр – соответственно орбитальная и вращательная скорости исследуемого объекта; D – диаметр объекта.

В частном случае центростремительное ускорение является ускорением силы тяжести (гравитации), а она, в свою очередь, определяется по второму закону Ньютона F1 = m⋅aцс. Адекватность модели подтверждается в работе [2]. Результаты расчёта по этой модели коэффициента G по формуле 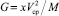[3], где x – радиус криволинейного движения; Vср = 0,5(Vорб + 2Vвр) [2, 3]; и ускорения силы тяжести сведены в табл. 1.

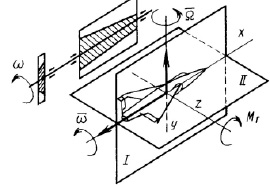
Рис. 1. Схема направлений действия гироскопического момента для одного из видов эволюции самолета [1]: w – угловая скорость ротора ГТД; W – угловая скорость эволюции летательного аппарата; Мг – гироскопический момент

Таблица 1

Результаты расчёта и справочные данные

Из табл. 1 видно, в частности, что результаты расчёта удовлетворительно сходятся со справочными данными. Следствие, вытекающее из модели: масса, сосредоточенная в центре вращения, не является причиной притяжения (гравитации), масса есть результат действия центростремительного ускорения (т.е. центростремительной силы).

В данной работе на основе модели центростремительного ускорения рассматривается взаимодействие внутренних сил, возникающих при вращении ротора.

В частности, при наличии эксцентриситета ротора а (несовпадении центра масс с осью вращения) возникает взаимодействие центробежной силы F и силы упругости ротора Fу (рис. 2) [1]. При установившемся движении имеет место равновесие сил

F = Fу,

или

m(a + y)w2 = cy, (2)

где m – масса ротора; a – эксцентриситет; y – прогиб вала ротора; w – угловая скорость ротора; c – коэффициент жёсткости вала на изгиб.

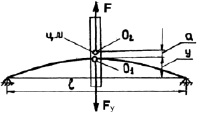
Рис. 2. Схема симметричного однодискового ротора [1]

Здесь внутренней силой сопротивления ротора является сила упругости материала вала, определяемая законом Гука

Fу/А = Е⋅Dr/r, (3)

где А – площадь рассматриваемого сечения, м2; Dr/r = 1 – относительное удлинение рассматриваемого объема тела; Е – модуль упругости.

Известно [4], что силы упругости в твердом теле обусловлены кулоновскими силами межатомного взаимодействия, поэтому

Fупр = Fкул,

где Fупр – сила упругости; Fкул – кулоновская сила взаимодействия зарядов.

Тогда модуль упругости E для кристаллических структур определяется по формуле [4]

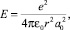
где e = 1,6⋅10–19 Кл – элементарный заряд, равный по модулю заряду электрона; p = 3,14; e0 = 8,85⋅10–12 Кл2/Н⋅м2 – электрическая постоянная; а0 – период кристаллической решётки; r – расстояние между ближайшими соседями – атомами.

Из формулы (3) находится приближённое соотношение между модулем упругости E и кулоновской силой Fкул

Fкул = А⋅Е. (4)

Модель центростремительного ускорения [2] используется для объектов с наноразмерами на основе вихревой модели элементарных частиц и атома [5]. В этом частном случае главные допущения в модели следующие:

1) материальная основа элементарных частиц (протонов, электронов и др.) – тёмная материя;

2) источником энергии вращения ядер атомов (протонов и нейтронов) и электронов в атомах является движение тёмной материи;

3) тёмная материя образует единое поле взаимодействий (электромагнитное суть гравитационное), в которой, как в «жидкости», формируется светлая материя;

4) центростремительная сила взаимодействия определяется по второму закону Ньютона F1 = m⋅aцс. Причём эквивалентом силы F1 является сила F2, определяемая законом Кулона, а также сила F3, определяемая законом всемирного тяготения.

Следствия моделирования:

а) физическая сущность гравитации – центростремительное ускорение, возникающее вследствие совместного поступательного и вращательного движения рассматриваемого объекта;

б) формулы Кулона F2 = e2/4p⋅e0⋅r2 и Ньютона F3 = (G⋅m⋅M)/r2 аналогичны по физической сущности [6], т.е. природой электростатического взаимодействия также является центростремительное ускорение (сила);

в) коэффициент G зависит от скорости движения тёмной материи Vср.

Подтверждением адекватности модели (а также единства физических законов в природе) является примерное равенство сил F1 ≈ F2 ≈ F3 в приведённых ниже примерах.

Пример 1. Определение силы химической связи (силы электростатического взаимодействия) в гексагональных кольцах графита на расстоянии а0 (рис. 3).

Обоснование расчёта силы химической связи (электростатического взаимодействия) приведено в работе [7]. Результаты расчёта сил F1, F2, F3 сведены в табл. 2. Причём расчётные значения центростремительного ускорения составляют в данном примере ацс = 16⋅1021 м/с, а коэффициента G = 24⋅1027 Нм2/кг2.

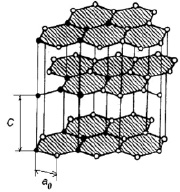
Рис. 3. Структура графита [8]

Таблица 2

Результаты расчёта и справочные значения

Из табл. 2 видно, в частности, что F1 ≈ F2 ≈ F3. Значения энергии химической связи Ехим также одного порядка, что подтверждает адекватность модели.

Пример 2. Определение силы химической связи (силы электростатического взаимодействия) между гексагональными слоями графита на расстоянии с (рис. 3). Результаты расчёта сил F1, F2, F3 сведены в табл. 3.

Из табл. 3 видно, в частности, что F1 ≈ F2 ≈ F3, что подтверждает адекватность модели. Сила Fкул (табл. 3) определяется по формуле (4) на основе справочного значения модуля упругости 18,0⋅109 Па между слоями графита [9]. Кроме того, приблизительное равенство модулей упругости 12,1⋅109…15,0⋅109 Па, рассчитанных по формуле (4) с использованием F1, F2, F3, также является косвенным подтверждением адекватности модели.

Таблица 3

Результаты расчёта и справочные значения

Пример 3. Определение силы химической связи (силы электростатического взаимодействия) в монокристалле водорода при температуре 4,2 К. Результаты расчёта сил F1, F2, F3 сведены в табл. 4.

Таблица 4

Результаты расчёта и справочные значения

Из табл. 4 видно, что F1 ≈ F2 ≈ F3, что подтверждает адекватность модели.

Пример 4. Определение силы связи в ядре атома изотопа водорода 12Н.

Для расчёта применяется единая модель, аналогичная определению силы химической связи (рис. 4) [7], но расчётные значения центростремительного ускорения составляют в данном примере ацс = 4,9⋅1028 м/с, а коэффициента G = 1,25⋅1026 Нм2/кг2. Взаимодействие нуклонов в ядре моделируется сферическими вихрями (по аналогии с моделью химической связи [7]). Штриховкой на рис. 4 показана область взаимодействия вихревых сфер нуклонов.

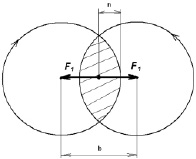
Рис. 4. Область взаимодействия вихревых сфер

Результаты расчёта сил F1, F2, F3 сведены в табл. 5.

Таблица 5

Результаты расчёта сильного взаимодействия

Из табл. 5 видно, в частности, что F1 ≈ F2, а сила F3 того же порядка, что F1, F2 – это подтверждает адекватность модели. Результаты расчёта подтверждают также, что модель соответствует основным свойствам ядерных сил [10], в частности:

1) ядерные силы являются силами притяжения (рис. 4);

2) ядерные силы являются короткодействующими (на рис. 4 расстояние b ≈ 10–15 м);

3) ядерные силы имеют неэлектрическую природу (на рис. 4 показано взаимодействие протона и нейтрона, при этом F1 ≈ F2).

Пример 5. Определение силы слабого взаимодействия при излучении (поглощении) фотона атомом водорода.

Определяется величина изменения DF соотношения между центростремительной Fцс и центробежной Fцб силами в атоме водорода при переходе его из возбуждённого в основное состояние. В частности, при излучении фотона с энергией 10,2 эВ, величина изменения DF = Fцб – Fцс = 3,8⋅10–9 Н. На рис. 5 точка А соответствует условию равновесия сил. Величина DF располагается правее точки пересечения А, т.к. Fцб > Fцс, что соответствует процессу излучения энергии. Левее точки пересечения А происходит процесс поглощения энергии атомом водорода.

Полученные результаты основаны на расчёте силы взаимодействия электрона с ядром в атоме водорода, которые приведены в табл. 6.

Из табл. 6 видно, что F1 ≈ F2 ≈ F3, что подтверждает адекватность модели и определяет возможность расчёта изменения сил при слабом взаимодействии.

Таким образом, разработанная модель объединяет четыре фундаментальных взаимодействия в одно. Иначе говоря, гравитационное, электромагнитное, ядерное и слабое взаимодействия имеют единую природу – вихревое центростремительное движение тёмной материи. Центростремительное ускорение (или сила) формируется в результате совместного орбитального и вращательного движения материи. Центростремительное вихревое движение тёмной материи формирует светлую материю. Причём многообразие светлой материи определяется дискретными уровнями энергии движущейся тёмной материи. Это не противоречит квантово-механическим представлениям. Кроме того, вихревая модель элементарных частиц и атомов [5] соответствует понятиям квантовой механики о том, что электрон «размазан» в атоме и присутствует во всех точках орбиты одновременно.

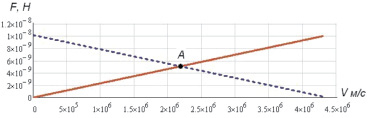
Рис. 5. Соотношение между центростремительной и центробежной силами:Fцб – сплошная линия; Fцс – пунктирная линия

Таблица 6

Результаты расчёта электростатического взаимодействия электрона ядром в атоме водорода

Частными следствиями модели являются: объяснение физической сущности антигравитации [3]; объяснение физической сущности некоторых механических явлений, которые имеют лишь математическую трактовку. Например, разработанная модель позволяет объяснить гироскопический эффект (рис. 6). Вследствие совместного переносного и относительного (орбитального и вращательного) движения ротора возникает центростремительная сила, которая обеспечивает устойчивость гироскопа к внешним воздействиям. В частности, не даёт ему упасть под действием силы тяжести mg (рис. 6).

Другим следствием является объяснение самоцентрирования ротора при превышении угловой скорости его вращения некоторой критической величины wкр [1]. Из выражения (2) следует, что прогиб вала ротора y принимает отрицательные значения при w > wкр – в этом суть математического объяснения самоцентрирования. В соответствии с разработанной моделью физическая сущность самоцентрирования заключается в следующем.

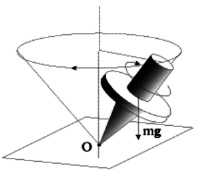
Рис. 6. Схема прецессии гироскопа

При w > wкр изменяется соотношение между центробежной силой Fцб

Fцб = m⋅(w2r) (5)

и центростремительной силой Fцс

Fцс = m⋅aцс,

где aцс определяется по формуле (1). При этом Fцс > Fцб, что приводит к самоцентрированию вращающегося ротора.

Выводы

1. Центростремительное ускорение объекта, совершающего совместное орбитальное и вращательное движение, определяется по формуле (1).

2. Центробежное ускорение этого же объекта определяется по формуле (5).

3. Часть физических явлений объясняется соотношением между центробежной и центростремительной силами. В частности, процессы излучения и поглощения энергии в атоме и его ядре, а также гироскопический эффект и самоцентрирование ротора при w > wкр.

Рецензенты:

Газизов Х.Ш., д.т.н., профессор кафедры сопротивления материалов, ФГБОУ ВПО УГАТУ, г. Уфа;

Целищев В.А., д.т.н., профессор, заведующий кафедрой прикладной гидромеханики, ФГБОУ ВПО УГАТУ, г. Уфа.

Работа поступила в редакцию 18.06.2013.

Библиографическая ссылка