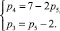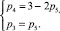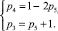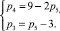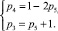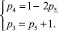Несмотря на то, что задача создания механизмов без избыточных связей была поставлена в полной мере профессором Решетовым Л.Н. [1] более чем пятьдесят лет назад, можно уверенно говорить о том, что исчерпывающе она не разрешена и до настоящего времени. Тем не менее, появилось четкое понимание того, что вполне работоспособными, самоустанавливающимися являются лишь механические системы, удовлетворяющие формуле А.П. Малышева, т.е. системы нулевого семейства. Остальные, хотя и оказываются часто вполне работоспособными, но при тщательном их исследовании нельзя не заметить, что они работоспособны лишь принудительно. Теоретически принужденность определяется тем, что эти системы прежде необходимо «насильно» ввести в некие пространства.
Избыточные связи в механических системах
Введение понятия избыточности т.е., избыточных связей, многими исследователями до настоящего времени приписывается А.П. Малышеву, что не соответствует истине. Об избыточных связях в современном понимании А.П. Малышев никогда не писал и даже не мог писать уже потому, что сама идея избыточности связей в его время не была осознана.
Покажем формулу подвижности в той записи, которую использовал А.П. Малышев в работе [2]
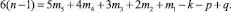
В современных обозначениях q – по Малышеву соответствует принятому позже W, т.е. W = q, если все mi заменить на pi, и исключить неподвижное звено из рассмотрения, тогда формула А.П. Малышева примет вид
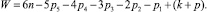
В этой формуле условия связи, «которые выпадают вследствие частностей» (k), а также связи, вводимые в изменяемые звенья (р), А.П. Малышев объяснил и показал, что они достаточно легко устранимы, и далее удалил их из своей формулы и уже в работе [3] ни о k, ни о р более речи он не вел
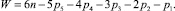 (1)
(1)
Рассмотрим, что имел в виду А.П. Малышев, записывая понятия связей, выпадающих вследствие частностей (k). В работе [2] он показал пример проходного кривошипно-ползунного механизма (рис. 1, а) с равными длинами кривошипа и шатуна (l1 = l2) и объяснил, что, если шарниры А и В совместить, то две пары В вращательная и поступательная выпадут и механизм превратится в кривошип (рис. 1, б). Это действительно частный случай и никакими формулами подвижности его изучить нельзя.
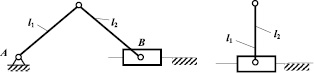
а б
Рис. 1. Выпадающие условия связи (k) по Малышеву
Что же касается связей р, то это понятие можно сопроводить рис. 2. Звено 2 здесь показывается как изменяемое. Ввести связь р по Малышеву, – это значит звенья 2′ и 2″ между собой соединить жестко. При этом и число звеньев, и число пар изменится, механизм станет работоспособным.
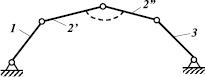
Рис. 2. Связи, превращающие изменяемые звенья в твердые
Таким образом, те связи, которые ныне получили название избыточных, в формуле Малышева не присутствуют и определены на её основании быть не могут.
Только после того, как В.В. Добровольский ввел понятие общих связей т, накладываемых на весь механизм в целом, стало возможным осознать, что все семейства механизмов, кроме нулевого, собираются с принуждением, и в них некие дополнительные связи неизбежны. Они могут быть устранены лишь путем изменения классов кинематических пар.
В своих исследованиях, основываясь на том, что классификация, предложенная академиком И.И. Артоболевским и профессором В.В. Добровольским, предусматривает деление механизмов на семейства по числу общих накладываемых связей, Н.И. Колчин показал, что число избыточных связей q в механизме определяется зависимостью [4]
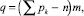
где т – число общих наложенных на механизм связей (по Добровольскому В.В.); п – число подвижных звеньев; Sрk – общее число используемых кинематических пар.
Именно после этой формулы Колчина, которая не была должным образом оценена многими исследователями, оказалось возможным определять число избыточных связей в конкретных механизмах. Однако эта формула никак не могла быть выведена из формулы Малышева (1). Покажем вывод формулы для определения q. Запишем формулу подвижности В.В. Добровольского
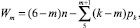 (2)
(2)
при (k – m) ≥ 1,
где Wm – подвижность конкретного семейства механизма; т – число общих наложенных на механизм связей; п – число подвижных звеньев; рk – кинематические пары k-го класса.
Раскроем скобки в правой части формулы (2)
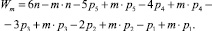
Сгруппируем члены
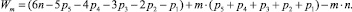
Первая скобка определяет формулу Малышева (1), эту скобку можно заменить на W0, т.е. на подвижность безызбыточной системы, или системы, не имеющей избыточных связей. Вторая скобка дает сумму используемых пар, вне зависимости от их класса, т.е.
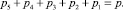
На основании проведенных рассуждений формулу (2) перепишем как
Wm = W0 + m·(p – n). (3)
Учтем, что Wm – W0 = q, тогда окончательно имеем
q = m·(p – n). (4)
Формула (4) полностью соответствует формуле Н.И. Колчина.
Она особенна тем, что абсолютно безупречно объясняет физическую сущность избыточных связей. Однако часто при решении сложных задач трудно или даже невозможно заранее определить, к какому семейству относится рассматриваемая механическая система, т.е. какое конкретное значение следует задать параметру т. В этом случае следует поступать так: решить (3) относительно q
q = Wm – W0,
задать нужное значение W (Wm = W) и, имея в виду, что W0 определяется по (1), получить число избыточных связей
q = 5р5 + 4р4 + 3р3 + 2р2 + + р1 – (6п – W). (5)
Но это уже не формула Малышева А.П. и пользоваться ею со ссылкой на него некорректно.
Завершим этот раздел кратким определением понятия избыточных связей в механических системах. Избыточными связями (q) в механических системах следует называть такие связи, которые вызывают дефицит подвижности в результате неизбежной принужденной сборки системы в случае, когда число звеньев, число и классы используемых кинематических пар не соответствуют самоустанавливающейся системе, описываемой формулой подвижности Малышева.
Устранение дефицита подвижности в плоских механизмах
Для устранения дефицита подвижности в плоских шарнирных механизмах предлагается методика, основанная на исследовании системы уравнений, описывающих механическую систему одновременно и как плоскую, и как пространственную, имеющей общий вид
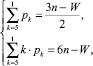 (6)
(6)
где W – подвижность кинематической цепи; k – класс кинематических пар (k = 5, 4, 3, 2, 1); n – число звеньев цепи.
Запишем систему (6) при условии, что пары p1 и p2 не будут использоваться при решении поставленной задачи, в силу сложности их реализации
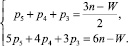 (7)
(7)
Решим систему (7) так, чтобы числа используемых кинематических пар определялись числом звеньев и подвижностью механизма. Выразим из первого уравнения системы (7) количество кинематических пар третьего класса
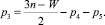 (8)
(8)
Подставим (8) во второе уравнение системы (7) и найдем, что
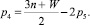 (9)
(9)
С учетом (9) преобразуем (8) так, чтобы значение p3 определялось однозначно числом пар p5
p3 = p5 – W. (10)
Объединим в систему уравнения (9) и (10)
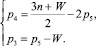 (11)
(11)
Теперь, задаваясь значениями чисел пар p5, зная число звеньев и подвижность исследуемой механической системы, по (11) определяются значения чисел кинематических пар p4, p3.
В работе [5] показано применение полученных зависимостей для решения задачи по исключению избыточных связей в плоском четырехзвеннике (п = 3), который является одноконтурным механизмом.
Все другие плоские механизмы при п > 3 выполняются не одноконтурными, в них могут находиться как неподвижные, так и подвижные замкнутые контуры. При устранении дефицита подвижности в таких механических системах необходимо добиваться такого расположения кинематических пар более высоких классов, чтобы безызбыточными были одновременно и все контуры, и механизм в целом.
В связи с этим предлагается рассматривать два вида избыточных связей – родовые и контурные. Родовые связи определяются исходя из того, к какому семейству (роду) относится механизм, а контурные – сложностью рассматриваемых контуров.
В данной методике не менее важной задачей является задача о разделении любой кинематической цепи на контуры. В связи с этим предлагается при разделении механизма на контуры выделять основной контур и дополнительные. Основным контуром будем называть последовательное соединение звеньев, включающее стойку, а дополнительным – группу звеньев, или звено, присоединяемых к основному контуру. Главное условие правильного выбора вида дополнительных контуров заключается в том, чтобы ни одно из звеньев механизма и ни одна из кинематических пар не использовались одновременно в основном и дополнительном контурах в пределах одного разделения.
Необходимо также отметить, что при решении задачи, связанной с устранением дефицита подвижности, нет надобности в использовании кинематических пар высоких классов в их конструктивно полном виде. Чтобы исключить избыточные связи, достаточно, например, позволить цилиндрической паре р4 движение с возможностью смещений звеньев только вдоль оси шарнира на некоторое расстояние s. Будем такие кинематические пары называть кинематическими парами квазивысоких классов.
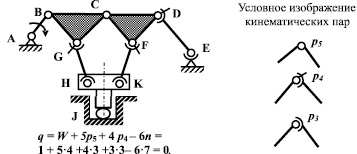
Рассмотрим решение поставленной задачи на примере плоского (m = 3) шарнирного (p5 = 10) восьмизвенного (n = 7) механизма пресса (W = 1) (рис. 3). Число избыточных связей в нём, определенное по (4) q = m·(p – n) = 3 (10 – 7) = 9.
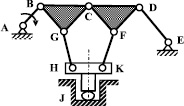
Рис. 3. Плоский шарнирный восьмизвенный механизм пресса
Сформулируем задачу так: найти для рассматриваемого механизма необходимое количество пар более высоких классов для замены ими пар p5 и такое их расположение, чтобы избыточные связи отсутствовали как в механизме в целом, так и в любом его контуре.
Приступая к выполнению поставленной задачи, подставляя значения n = 7 и W = 1, найдем по (11) систему уравнений для определения родовых решений
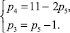 (12)
(12)
Система (12) имеет пять целочисленных положительных родовых решений
1. p5 = 5, p4 = 1, p3 = 4; (12.1)
2. p5 = 4, p4 = 3, p3 = 3; (12.2)
3. p5 = 3, p4 = 5, p3 = 2; (12.3)
4. p5 = 2, p4 = 7, p3 = 1; (12.4)
5. p5 = 1, p4 = 9, p3 = 0. (12.5)
Если говорить о создании механизма без дефицита подвижности в целом, то формально каждое из приведенных решений является удовлетворительным. Однако при этом не гарантируется, что каждый из контуров механизма будет безызбыточным.
Для гарантированного устранения дефицита подвижности разработан метод адресной замены шарниров кинематическими парами более высоких классов, состоящий из шести последовательных этапов решения.
Первый этап заключается в представлении механизма несколькими разделениями на контуры. Необходимое и достаточное число разделений определяется одним из десяти параметров [6], характеризующих любую кинематическую цепь, а именно, числом выходов цепи δ. В случае если механизм содержит замкнутые изменяемые контуры α, то между γ, α и δ появляется взаимосвязь вида
γ = δ + α, (13)
где под параметром γ понимается число ветвей, которое было бы в цепи при условии, если бы строилась цепь без изменяемых замкнутых контуров. Параметр этот можно найти из следующих соображений: в цепи, построенной без изменяемых замкнутых контуров, число ветвей – есть число свободных пар, которое определится, если из общего числа кинематических пар цепи вычесть все пары, которые образовали (n – 1) звеньев, будучи присоединёнными к базовому τ – угольнику, т.е.
γ = p – (n – 1). (14)
Выразим из (13) число выходов цепи и с учётом зависимости (14) получим
δ = p – (n – 1) – α. (15)
Рассматриваемый механизм содержит один изменяемый замкнутый контур (α = 1), семь подвижных звеньев и десять шарниров, следовательно, число выходов по (15) δ = 10 – 6 – 1 = 3. Таким образом, исследуемый механизм должен иметь три разделения, каждое из которых представим основным и дополнительными контурами (рис. 4).
1а) 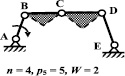 1б)
1б)  1в)
1в) 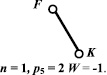
2а) 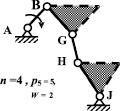 2б)
2б) 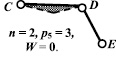 2в)
2в) 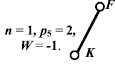
3а) 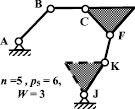 3б)
3б) 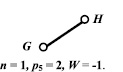 3в)
3в) 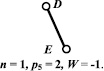
Рис. 4. Второе (2,a, 2,б, 2,в) и третье (3,а, 3,б, 3,в) разделения восьмизвенного механизма пресса на контуры
Во втором этапе для каждого разделения определяются необходимые значения чисел кинематических пар более высоких классов для замены ими шарниров. Приступим к решению этого этапа и рассмотрим основной контур ABCDE первого разделения (рис. 4, 1.а), который состоит из четырёх подвижных звеньев (n = 4) и пяти шарниров (p5 = 5). Подвижность контура W = 2. Подставляя значения n и W в (11), получим систему:
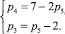 (16)
(16)
Система (16) имеет два варианта положительных целочисленных решений
1. p5 = 3, p4 = 1, p3 = 1; (16.1)
2. p5 = 2, p4 = 3, p3 = 0. (16.2)
После выделения основного контура, первое разделение представлено дополнительным контуром JHG и звеном FK, контур JHG содержит в своём составе два подвижных звена (n = 2) и три шарнира (p5 = 3), представляя группу нулевой подвижности (W = 0).
Система (11) для контура JHG при указанных условиях примет вид
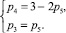 (17)
(17)
Она дает единственный вариант решения
1. p5 = 1, p5 = 1, p5 = 1. (17.1)
Для звена FK по (11) получаем систему
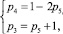 (18)
(18)
которая также имеет единственный вариант решения
1. p5 = 0, p4 = 1, p3 = 1. (18.1)
Перейдём к третьему этапу, который заключается в нахождении комплексного решения, предусматривающего суммирование полученных результатов решения для каждого контура в рассматриваемом разделении.
Таких решений получается два. Первое представляет сумму решений (16.1), (17.1) и (18.1); второе – (16.2), (17.1) и (18.1)
1. p5 = 4, p4 = 3, p3 = 3; (19.1)
2. p5 = 3, p4 = 5, p3 = 2. (19.2)
Для второго и третьего разделений восьмизвенного механизма пресса проведём аналогичные расчёты и представим результаты расчета в табл. 1.
Основной контур второго разделения ABGHJ (рис. 4, 2.а) cодержит в своём составе четыре звена (n = 4), пять кинематических пар пятого класса (p5 = 5) и имеет подвижность W = 2. После определения основного контура в механизме, выделяется дополнительный (рис. 4, 2.б) контур CDE (n = 3, p5 = 3, W = 0) и звено FK (n = 1, p5 = 2, W = –1).
Третье разделение содержит основной контур ABCFKJ (n = 5, p5 = 6, W = 3) (рис. 4, 3.а) и два звена GH и DE (n = 1, p5 = 2, W = –1) (рис. 4, 3.б и 4, 3.в).
Во второй колонке таблицы приведены системы уравнений, полученные при постановке в (11) значений чисел звеньев и подвижности для каждого контура или звена, по которым определяются числа используемых кинематических пар (четвёртая колонка). Комплексные решения для разделений приведены в пятой колонке таблицы.
Результаты решений для второго и третьего разделений восьмизвенного механизма
|
Разделения |
Система уравнений (11) |
Кол- во решений |
Решения системы уравнений |
Комплексные решения разделений |
|
2.а |
|
2.а. 1 2.а. 2 |
p5 = 3, p4 = 1, p3 = 1, p5 = 2, p4 = 3, p3 = 0. |
1. p5 = 4, p4 = 3, p3 = 3, 2. p5 = 3, p4 = 5, p3 = 2, |
|
2.b |
|
2.б. 1 |
p5 = 1, p4 = 1, p3 = 1. |
|
|
2.с |
|
2.в.1 |
p5 = 0, p4 = 1, p3 = 1. |
|
|
3.а |
|
3.а. 1 3.а. 2 |
p5 = 4, p4 = 1, p3 = 1, p5 = 3, p4 = 3, p3 = 0. |
1. p5 = 4, p4 = 3, p3 = 3, 2. p5 = 3, p4 = 5, p3 = 2. |
|
3.b |
|
3.б.1 |
p5 = 0, p4 = 1, p3 = 1. |
|
|
3.с |
|
3.в.1 |
p5 = 0, p4 = 1, p3 = 1. |
Под комплексным решением по-прежнему, понимаются алгебраические сложения полученных решений для принятых разделений. Так, для второго разделения первое комплексное решение представляет сумму (2.а.1, 2.б.1 и 2.в.1), второе комплексное решение – (2.а.2, 2.б.1 и 2.в.1). Для третьего разделения, которое также имеет два комплексных решения – это сумма (3.а.1 и 3.б.1, 3.1.в) и (3.а.2 и 3.б.1, 3.1в).
Полученные комплексные решения первого, второго и третьего разделений механизма совпадают с двумя родовыми решениями (12.2 и 12.3), это решения
p5 = 4, p4 = 3, p3 = 3,
p5 = 3, p4 = 5, p3 = 2.
Таким образом, четвёртый этап заключается в сравнении комплексных решений разделений между собой и с родовыми решениями с целью определения совпадающих решений, которые и должны использоваться при исключении избыточных связей как в самом механизме, так и в его контурах.
Дальнейшее решение проведём по варианту p5 = 4, p4 = 3, p3 = 3. Поставим теперь задачу так: найти, какие именно (адресно) шарниры исследуемого механизма необходимо заменить на пары квазивысоких классов и на какие именно. Не решив такой задачи, гарантировать одновременно безызбыточность механизма и каждого контура невозможно. Поступим так: идентифицируем все кинематические пары механизма (см. рис. 1), обозначив их соответствующими буквами, и запишем алгебраические уравнения, соответствующие принятому решению, причём в левых частях уравнений, в виде суммы обозначенных буквами кинематических пар, входящих в контуры рассматриваемых разделений, а в правых – в виде суммы соответствующих решений (см. таблицу). Первое уравнение системы должно соответствовать принятому родовому решению механизма, т.е.
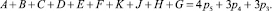
Составим уравнение для основного контура первого разделения (рис. 4, 1.а) по решению (16.1)
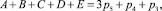
для дополнительного контура первого разделения JHG (рис. 4, 1.б) по решению (17.1)
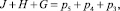
для звена FK первого разделения (рис. 4, 1.в) по решению (18.1)
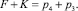
При составлении уравнений для второго разделения используются те решения, которые при сложении дают p5 = 4, p4 = 3, p3 = 3, они в таблице подчёркнуты, тогда получим для контура ABGHJ по (2.а.1)
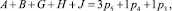
для контура CDE по (2.b.1)

для звена FK по (2.в.1)
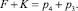
Аналогичные уравнения в третьем разделении примут вид: для основного контура ABCFKJ по решению (3.а.1)
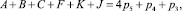
для звеньев GH и DE по (3.b.1) и (3.с.1), соответственно
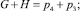
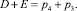
Объединим полученные уравнения в одну систему.
Приступим к решению системы (20), для этого подставим шестое уравнение системы (20.6) во второе (20.2) и получим, что А + В = 2p5. Значит, в этих точках должны находиться кинематические пары пятого класса. Подставляя (20.9) в третье уравнение (20.3), находим, что J = p5, тогда в рассматриваемой системе получаются три тождественных уравнения – это (20.3), (20.5) и (20.9) G + H = р4 + р3, следовательно G = p4, H = p3, либо G = p3, H = p4. Из (20.6), учитывая, что D + E = p4 + р3, получаем С = р5. После проведенного решения система (20) имеет по три тождественных уравнения F + K = р4 + р3 (четвёртое, седьмое, восьмое) и D + E = p4 + р3 (второе, шестое, десятое).
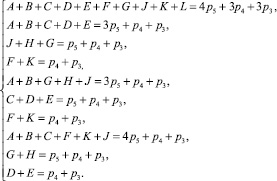 (20)
(20)
Таким образом, в этих точках будут располагаться пары третьего или четвёртого классов, т.е. F = p4, K = p3, либо F = p3, а K = p4 и, аналогично, E = p4, D = p3, или E = p3, D = p4. Безызбыточность механизма при замене пар p3 на p4 в этом случае не нарушается.
По результатам полученного решения на рис. 5 приведён рычажный механизм пресса, не содержащий избыточных связей.
а б
Рис. 5. Рычажный механизм пресса без избыточных связей
Покажем, что избыточные связи отсутствуют и в контурах механизма.
Контур ABCDE.
Подвижность контура
W = 6п – 5р5 – 4р4– 3р3 = 6∙4 – 5∙3 + 4∙1 + 3∙1 = 1,
число избыточных связей
q = 5р5 + 4р4 + 3р3 + 2р2 + р1 – (6п – W) = 5∙3 + 4∙1 + 3∙1 – (6∙4 – 1) = 0.
Контур ABGHJ.
Подвижность контура
W = 6п – 5р5 – 4р4– 3р3 = 6∙4 – 5∙3 + 4∙1 + 3∙1 = 1,
число избыточных связей
q = 5р5 + 4р4 + 3р3 + 2р2 + р1 – (6п – W) = 5∙3 + 4∙1 + 3∙1 – (6∙4 – 1) = 0.
Контур EDFКJ.
Подвижность контура
W = 6п – 5р5 – 4р4– 3р3 = 6∙4 – 5∙1 + 4∙2 + 3∙2 = 5,
число избыточных связей
q = 5р5 + 4р4 + 3р3 + 2р2 + р1 – (6п – W) = 5∙1 + 4∙2 + 3∙2 – (6∙4 – 5) = 0.
Анализ полученных результатов, проведённый после решения по замене шарниров на пары p3 и p4 в плоском восьмизвенном механизме пресса, дает возможность сформулировать, по крайне мере, три важных вывода:
1. При разделении на контуры суммарная подвижность выделяемых контуров должна быть равна подвижности исследуемой кинематической цепи, т.е. для механизмов W = 1.
2. Необходимое и достаточное количество разделений равно числу выходов (δ) в механизме.
3. Сложность выделенного основного и дополнительных контуров определяется структурой механизма.
Рецензенты:
Живаго Э.Я., д.т.н., профессор, зав. кафедрой «Теоретическая механика», ФГОБУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк;
Никитин С.Г., д.т.н., профессор, зав. кафедрой «Сопротивления материалов и строительной механики», ФГОБУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.
Работа поступила в редакцию 18.03.2013
Библиографическая ссылка
Гудимова Л.Н., Дворников Л.Т. ПРОБЛЕМЫ ИСКЛЮЧЕНИЯ ИЗБЫТОЧНЫХ СВЯЗЕЙ В ПЛОСКИХ ШАРНИРНЫХ МЕХАНИЗМАХ // Фундаментальные исследования. 2013. № 6-1. С. 24-32;URL: https://fundamental-research.ru/ru/article/view?id=31408 (дата обращения: 05.07.2025).