В настоящее время цифровая обработка сигналов (ЦОС) занимает основное положение в системах передачи и обработки информации. Эффективность ЦОС полностью зависит от объема вычислений, который определяется математической моделью цифровой обработки сигналов. Большое научное и практическое значение имеют вопросы выбора элементной базы для создания современных систем ЦОС. Обеспечить высокие требования к производительности можно только за счет совместного применения нетрадиционных алгебраических систем и параллельных методов обработки информации, реализуемых на основе нейросетевых технологий. Это позволит обеспечить обработку большого массива данных в реальном масштабе времени[1,2,4].
Новым направлением в разработке сумматоров по модулю два может служить изменение функции активации нейронной сети. Предлагается использовать двухслойную нейронную сеть, в которой в качестве функции активации используется треугольная функция активации - tribas, согласно условия (1)
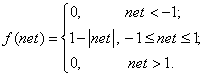 (1)
(1)
Для реализации нейросетевой модели сумматора по модулю два с использованием треугольной функции активации для двухвходового вектора требуется один нейрон. Математическая модель нейроподобного сумматора по модулю два показана на рисунке 1.

Рис. 1. Нейросетевая модель двухвходового сумматора по модулю два с использованием треугольной функции активации
В работе [3] представлен алгоритм разработки нейросетевой модели сумматора по модулю два с использованием треугольной функции активации для вектора входа состоящего из n элементов. Число слоев в построенной по данному алгоритму модели будет равно N= n-1, число нейронов в слое рассчитывается из условия ![]() , где
, где ![]() . Так как для нечетного n число слоев будет четно, то, просуммировав попарно число нейронов первого и последнего слоя
. Так как для нечетного n число слоев будет четно, то, просуммировав попарно число нейронов первого и последнего слоя ![]() , второго и предпоследнего слоя
, второго и предпоследнего слоя ![]() и т.д., получаем общее число нейронов равное
и т.д., получаем общее число нейронов равное
![]() (2)
(2)
Для четного n число слоев нейронной сети нечетно, следовательно, нейронная сеть содержит нейронов
![]() (3)
(3)
Основным недостатком данного алгоритма являются значительные аппаратурные затраты. С целью уменьшения аппаратурных затрат при построении многовходового сумматора по модулю два на основе нейросетевого базиса в работе [1] предложено использовать каскадную организацию вычислительного устройства. В этом случае входной слой, реализует операцию нахождения суммы по модулю два значений каждой пары входов и передает полученные промежуточные значения на второй слой нейронов. При этом значения входа нейрона, у которого нет пары, поступает в следующий слой без изменений. Данная процедура повторяется и для последующих слоев, до тех пор, пока не получится слой, состоящий из одного нейрона, выход которого и будет конечным результатом. С целью дальнейшего снижения аппаратурных затрат была предложена модель нейронной сети, структура которой представлена на рисунке 2.
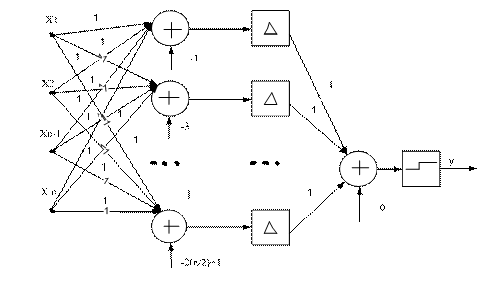
Рис. 2. Трехслойная нейронная сеть сумматора по модулю два.
Входной слой в процессе вычисления значения суммы по модулю два n-разрядного вектора не участвует, а осуществляет перераспределение данных, поступивших на входы нейронной сети. Скрытый слой, содержащий по одному нейрону для каждого возможного нечетного значения суммы элементов вектора входа причем смещение нейрона равно значению возможной нечетной суммы со знаком минус. Синаптические веса между нейронами входного и скрытого слоя равны 1. В качестве функции активации используется пороговая функция, что позволит повысить скорость обработки сигнала в выходном слое. Выходной слой состоит из одного нейрона, синаптические веса которого равны 1, а смещение 0.
Таким образом очевидно, что представленная нейросетевая модель сумматора по модулю два с использованием треугольной функции активации для вектора входа состоящего из n разрядов является наиболее привлекательной. При этом обеспечивается выполнение процедуры всего за две итерации, требуя на это равное количество аппаратурных затрат.
СПИСОК ЛИТЕРАТУРЫ:
- Элементы компьютерной математики и нейроноинформатики /Червяков Н.И., Калмыков И.А., Галкина В.А., Щелкунова Ю.О., Шилов А.А.; Под ред. Н.И. Червякова. - М.: Физматлит, 2003. - 216 с.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов /Под ред. Н.И. Червякова - М: Физматлит, 2005.-276 с.
- Шилов А.А., Калмыков И.А., Подопригора Н.Б., Брыкалова О.В. Нейронная реализация сумматора по модулю два для входного вектора размерностью n. Тезисы докладов Международной научно-технической конференции «Физика и технические приложения волновых процессов», г. Самара, 2003. - С. 167.
- Калмыков И.А., Тимошенко Л.И., Лободин М.В., Сагдеев А.К. Реализация ортогональных преобразований сигналов в расширенных полях Галуа / «Современные наукоемкие технологии», № 4, 2006 г.- С 54-56.
Библиографическая ссылка
Калмыков И.А., Тимошенко Л.И. НЕЙРОСЕТЕВЫЕ МОДЕЛИ МНОГОВХОДОВЫХ СУММАТОРОВ ПО МОДУЛЮ ДВА // Фундаментальные исследования. 2008. № 3. С. 73-74;URL: https://fundamental-research.ru/ru/article/view?id=2784 (дата обращения: 04.07.2025).



