Уравнения Максвелла дают следующее выражение для проникновения электромагнитной волны в металл при однородной проводимости σ и переменной магнитной проницаемости μ[1]:
(1)
Простое решение (1) получается в одномерном случае при постоянном μ и синусоидальном магнитном поле у поверхности полуограниченного тела H(0)=H0cos(wt).
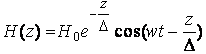(2)
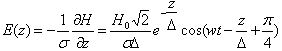(3)
где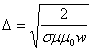 
-толщина скин-слоя. Поверхностная плотность активной мощности, выделяемой в металле в среднем за период, определяется выражением:
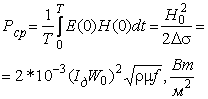(4)
где 
- действующее значение тока, 
- плотность намотки витков (1/м), 
- Ом*м, 
-Гц. Из-за сдвига фаз на π/4 между E и H коэффициент мощности равен
α= 
. Согласно (4) увеличение напряженности поля H0 существенно увеличивает плотность вводимой мощности, однако при этом μ начинает зависеть от H и рассматриваемое приближение неприменимо. Точная зависимость кривой намагничивания ферромагнетика может содержать до 10 параметров [2]. При практических расчётах её аппроксимируют отрезками парабол, зависимости H(t) заменяются их первыми гармониками, что позволяет исключить зависимость от времени[3]. Для приближенной оценки выделенной мощности предлагается использовать формулу(4) с увеличенным в 1,36 раза численным коэффициентом и "µ", определяемой по действующему значению напряжённости магнитного поля у поверхности ферромагнетика [4]. Коэффициент мощности "α" в режимах с насыщением не оценивался.
Рассмотрим прямое численное решение(1) без разложения по гармоникам при заданной зависимости µ(H) определяемой типом материала. Для большинства конструкционных сталей в сильных полях магнитную проницаемость можно аппроксимировать следующим выражением:
(5)
где Bm и Hc константы. Для сталей ст.10, ст.3 Bm≈2Тл , Hc ≈2*103 А/м. Тогда в плоском случае при достаточной толщине металла уравнение(1) запишется:
(6)
Переходя к безразмерным величинам будем иметь:
(7)
где 
;
. Для электрического поля и вводимой мощности получим:
(8)
(9)
(10)
На рис. 1,2 представлены численные решения значений E/(0,τ), H/ (0,τ), а также Pср и a при различных значениях Hmax/Hc.
Зависимости H/(0,τ)- 1,2,3 при синусоидальной форме E/(0,τ)-4(относительные величины): 1-E0/=0.1; Hm/(0,τ)=0.15; Pср/=0.011; α=0.72; 2- E0/=20; Hm/(0,τ)=120; Pср/=980; α=0.86;3-модель 
;
;α=0.89.
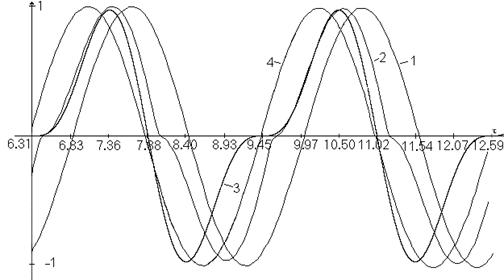
Рисунок 1.
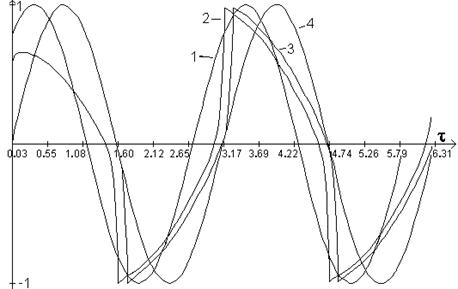
Рисунок 2.
Зависимости E/(0,τ) -1,2,3 при синусоидальной форме H/(0,τ)-4: 1- H/0=0.1; E/(0,τ)-0.138; P/ср=0,0049; α=0.72; 2- H/0=50; E/(0,τ)-15.1; P/ср=280; α=0.82; 3-модель E/ 2(0,τ)=4H/0; P/ср=0.85H0/ 3/2; α=0.85.
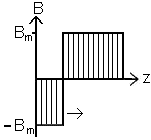
Можно предложить простую физическую модель проникновения магнитного поля в ферромагнетик в режиме с насыщением. Индукция поля значением B=Bm проникает вглубь ферромагнетика в соответствии с уравнением:
. При смене знака E(0,t) на границе металла B скачком меняет знак и это противоположное значение движется внутрь, в то время как движения в глубине прекращается. Ток протекает по внешней расширяющейся области проникновения с однородной по глубине плотностью j=σE. Полный ток на единицу длины, равный напряженности магнитного поля у поверхности, равен I(t)=H(0,t)=σzE(0,t). При задании на границе Е(0,t)=E0sinwt, получаем 
;
;
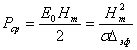, где 
- амплитуда H(0,t);
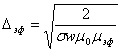- эффективная толщина скин-слоя при магнитной проницаемости 
, определяемой по амплитуде H(0,t). При заданной на границе H(0,t)=H0sinwt получаем 
, 
, 
.
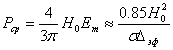Отметим, что в обоих случаях сохраняется соотношение между Hm и Em и глубина проникновения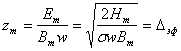 
. Модельные значения H(0,t) и E(0,t) показаны на рис.1,2. При Hm/Hc>50 они приближаются к результатам численного расчёта. Таким образом, глубокое насыщение ферромагнетика позволяет увеличить как удельную выделяемую мощность, так и коэффициент мощности.
Исследования, описанные в данной работе, были проведены в рамках проекта PZ-013-02, поддерживаемого совместно Американским фондом гражданских исследований и развития (АФГИР), Министерством образования РФ и правительством Республики Карелия.
Литература:
- Л.Д.Ландау, Е.М.Лифшиц "Электродинамика сплошных сред",М.,Наука,1987,620с.
- Набиев Н.А., Гулиев З.А.,Гаджибалаев Н.М., "Электричество",2002,№3, с.54-57.
- В.В.Сухоруков "Математическое моделирование электромагнитных полей в проводящих средах", М., Энергия,1975,150с.
- Установки индукционного нагрева" под редакцией А.Е.Слухоцкого, Л.,Энергоиздат, 1981,328с.
Работа представлена на научную конференцию с международным участием «Технологии 2004» (18-25 мая 2004г. Турция г.Анталия)