Для исследования различных характеристик плёнок большой интерес представляют данные о динамике адсорбированных атомов. Атомы на поверхности находятся в иной координации, чем в объёме, что приводит к изменению динамических постоянных связей их с соседними атомами, а, следовательно, к изменению амплитуд и изотропности их колебаний.
Адекватное описание поведения адсорбированных атомов достигается не только при учёте влияния латерального взаимодействия частиц на перестройку спектра фононов в плёнке, но и влияния поля подложки. Основой для построения самосогласованной теории может служить метод двухвременных функций Грина, являющийся современным языком изучения коллективных возбуждений в конденсированных системах.
Рассмотрим простейшую модель, в которой пленка представлена в виде динамической двумерной решетки на подложке, испытывающей фазовый переход I рода. Гамильтониан такой модели определим классическим образом:
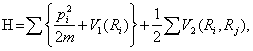 (1)
(1)
где ![]() - одночастичный псевдопотенциал с собственной симметрией, описывающий силовое поле подложки,
- одночастичный псевдопотенциал с собственной симметрией, описывающий силовое поле подложки, ![]() - парный межчастичный потенциал взаимодействия частиц в пленке.
- парный межчастичный потенциал взаимодействия частиц в пленке.
Общий вид потенциалов ![]() и
и ![]() зависит от характера взаимодействия плёнки с подложкой и латерального взаимодействия в плёнке. Если потенциал
зависит от характера взаимодействия плёнки с подложкой и латерального взаимодействия в плёнке. Если потенциал ![]() выбрать в виде:
выбрать в виде:
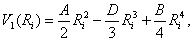 (2)
(2)
где A, D, B - положительные зависящие от температуры подложки функции, то получим ангармонический одночастичный псевдопотенциал поля подложки
Аналогично для парного межчастичного потенциала возможно следующее представление:
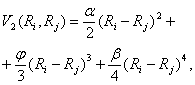 (3)
(3)
где α, β, и φ - силовые константы, определяющие взаимодействие соседних частиц пленки.
Соотношения (1), (2), и (3) определяют модель ангармонически связанных осцилляторов - адсорбированных атомов - в ассиметричной потенциальной яме поля подложки - модель {φ3-φ4}. В отличии от симметричной модели гармонически связанных осцилляторов эта модель для случая d ≥2 будет иметь возможность описывать «метастабильные» состояния атомов в локальных минимумах, а значит описывать СФП I рода.
В зависимости от соотношения силовых констант потенциалов V1(Ri) и V2(Ri, Rj) возможны различные случаи расположения потенциалов друг относительно друга. Если координаты локальных минимумов совпадают, параметры решетки и пленки соразмерны, происходит фазовый переход в соразмерную фазу. Тогда параметр решётки образующейся на поверхности структуры будет совпадать с параметром решётки подложки. Если же координаты локальных минимумов не совпадают, имеет место фазовый переход в несоразмерную фазу.
Исследование предложенной модели методом функций Грина позволяет проследить влияние поля подложки на различные динамические и термодинамические свойства пленки, проследить особенности структурных фазовых переходов. Увеличение гармонической константы потенциала подложки А приводит к увеличению температуры перехода, однако уменьшает скачок среднего расстояния. Увеличение же ангармонической константы D потенциала подложки, напротив, уменьшает температуру перехода, одновременно увеличивая скачок среднего расстояния.
Получено выражение, определяющее спектр возможных возбуждений в пленке вблизи точки фазового перехода. Наличие поля подложки приводит к сдвигу дисперсионных кривых вдоль оси ω; латеральное взаимодействие между частицами плёнки влияет на быстроту изменения частоты с изменением волнового вектора, а потому увеличение латерального взаимодействия приводит к увеличению щели между фононными спектрами в стабильной и метастабильной фазе.
Скачкообразное изменение среднего расстояния атома плёнки приводит к скачкообразному изменению энергии. При этом величина скачка энергии зависит от ангармонической константы потенциала подложки, тогда как зависимость от гармонической константы выражена слабо. Аналитический расчёт теплоёмкости даёт типичную для теории Ландау картину скачков теплоёмкости для разных фаз.
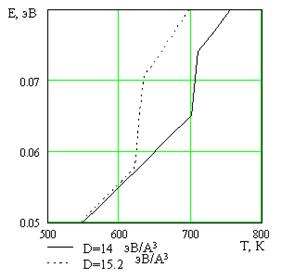
Рисунок 1. Температурная зависимость внутренней энергии на одну частицу
при разных ангармонических константах D потенциала подложки
Таким образом, предложенная модель позволяет проследить структурные фазовые переходы в плёнках, а также рассчитать интересующие различные динамические и термодинамические свойства с учётом летерального взаимодействия между частицами и влияния поля подложки.



