Применение полиномиальной системы классов вычетов (ПСКВ) позволяет не только повысить скорость работы вычислительных устройств, но и обеспечивать требуемый уровень надежности функционирования специализированных процессоров (СП) [1,2]. Рассматривая процедуры обнаружения и коррекции ошибок, нельзя не отметить возможность применения для данных процедур позиционной характеристики - нормированного следа.
Теорема. Если в системе ПСКВ, содержащей k информационных и r избыточных оснований, в результате нулевизации A(z) получен нормированный след полинома
, (1)
то номер интервала, в который попадет ошибочный полином A*(z), равен:
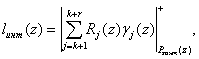(2)
где 
;
.
Доказательство. Докажем в начале, что если хотя бы один 
, где j =k+1,..., k+r, то полином A*(z) является запрещенным. Заменим произведение r избыточных оснований ПСКВ одним составным модулем 
. Тогда полином A(z)= 
примет вид:
, (3)
где 
Если в кодовой комбинации A(z) произошла ошибка, то результатом операции параллельной нулевизации A*(z) с использованием псевдоортогональных базисов Aik(z) будет отличный от нуля нормированный след:
(4)
где 
; 
- ортогональный базис безизбыточной ПСКВ.
С другой стороны, согласно китайской теореме об остатках (КТО):
, (5)
где 
; Uj(z) - ортогональный базис ПСКВ с основаниями pk+1(z),..., pk+r(z).
Так как 
, то хотя бы один 
отличен от нуля. Таким образом, если в результате нулевизации A*(z) и псевдоортогональных базисов получен след полинома
,
то полином - ошибочный.
Докажем теперь, что величина интервального номера lинт(z) определяется выражением (2). Пусть в результате процедуры нулевизации полинома A*(z) получим нормированный след:
отличный от нуля. Известно
, (6)
где 
;
-глубина ошибки по i-ому основанию.
При этом: 
Тогда на основании выражения (17) имеем:
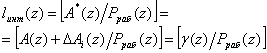. (7)
Согласно КТО и с учетом:
,
имеем:
. (8)
Подставляем (8) в равенство (7) получаем:
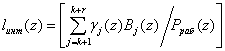. (9)
Учитывая подобие ортогональных базисов и делимость без остатка ортогональных базисов контрольных оснований на рабочий диапазон, имеем:
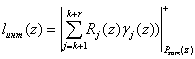, (10)
где 
.Доказательство закончено.
В работе [3] представлена организация сети нейронной логики, реализующей вычисление номера согласно (10) расширенном поле Галуа FD(24). С целью сокращения схемных затрат целесообразно перейти к многомерной обработке данных. Тогда
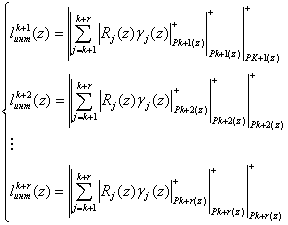(11)
Таким образом, применение выражения (11) позволяет осуществить процедуру поиска и коррекции ошибок с использованием нормированного полинома.
Выводы: Из полученных данных наглядно видно, что вычислительное устройство, реализующее алгоритм (11), обеспечивает наибольшую эффективность при контроле и исправлении ошибок, возникающих в процессе функционирования спецпроцессора.
СПИСОК ЛИТЕРАТУРЫ
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронной сети для коррекции ошибок в непозиционном коде расширенного поля Галуа/Нейрокомпьютеры: разработка, применение. №8-9, 2003. С. 10-16.