Изучение движения мельчайших твердых частиц в пористом грунте является актуальной задачей при проектировании и строительстве туннелей и гидротехнических сооружений. При фильтрации суспензии часть частиц проходит через пористую среду вместе с потоком несущей жидкости, а часть застревает в порах фильтра. Долговременная глубинная фильтрация, сопровождающаяся образованием осадка во всей пористой среде, а не только в ее поверхностном слое, существенно влияет на свойства горных пород и почвенных слоев [1]. В разнообразных технических и биологических системах очистки поверхностных и сточных вод и жидких промышленных отходов происходит захват частиц при движении суспензии через фильтрующую среду [2].
В работе рассматривается математическая модель движения частиц в фильтре, основанная на механико-геометрическом взаимодействии частиц с пористой средой [3]. Предполагается, что частицы свободно проходят через поры большого размера и застревают на входе пор, если диаметр частицы больше диаметра поры. Осажденная частица не может быть выбита из поры потоком жидкости или другой частицей, и навсегда остается в поре. С ростом осадка количество свободных малых пор сокращается и скорость образования осадка замедляется. Если все поры малого размера заблокированы частицами, концентрация осадка S достигает максимально возможного предельного значения SM. Коэффициент пропорциональности Λ(S) между скоростью роста осадка и концентрацией взвешенных частиц, обращающийся в ноль при блокировании всех малых пор S = SM, называется блокирующим коэффициентом фильтрации.
Для различных моделей фильтрации стационарного потока суспензии в пористой среде получены точные и асимптотические решения [4–9]. При отсутствии аналитических решений используются численные расчеты [10–13].
Стандартные модели фильтрации суспензии в пористой среде предполагают, что на вход фильтра подается суспензия с взвешенными частицами постоянной концентрации. В работе рассматривается фильтрация нестационарного потока суспензии. Приводится решение одномерной задачи фильтрации монодисперсной суспензии в пористой среде. Производится расчет полного осадка в пористой среде в случае линейного блокирующего коэффициента фильтрации для различных распределений концентрации взвешенных частиц на входе фильтра.
Постановка задачи
Рассмотрим основные уравнения, описывающие динамику взвешенных и осажденных частиц суспензии в фильтре длиной 1. Обозначим через C(x, t) концентрацию взвешенных частиц, пусть S(x, t) – концентрация осажденных частиц. Концентрации частиц удовлетворяют уравнению непрерывности, которое с учетом неподвижности осадка в простейшем случае имеет вид
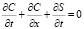 . (1)
. (1)
Рост осадка пропорционален концентрации взвешенных частиц, из которых он образуется, а также зависит от текущей величины осадка S(x, t): чем больше пор малого диаметра закрыто частицами, тем меньше скорость роста осадка
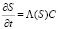 . (2)
. (2)
Здесь Λ(S) > 0 при S ≥ 0.
Система уравнений (1), (2) рассматривается в области 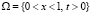 . Краевые условия для системы (1), (2) ставятся на входе фильтра x = 0 и в начальный момент времени t = 0:
. Краевые условия для системы (1), (2) ставятся на входе фильтра x = 0 и в начальный момент времени t = 0:
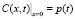 ; (3)
; (3)
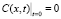 ;
; 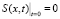 . (4)
. (4)
Условия (4) означают, что в начальный момент пористая среда не содержит взвешенных и осажденных частиц. Суспензия переменной концентрации начинает поступать на вход фильтра в момент t = 0 и движется в пористой среде со скоростью v = 1. Характеристика t = x – фронт концентраций взвешенных и осажденных частиц является подвижной границей суспензии. В области пустой пористой среды 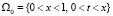 решение нулевое; в области суспензии
решение нулевое; в области суспензии 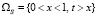 решение положительно.
решение положительно.
Решение на входе фильтра
Уравнение (2) на входе фильтра x = 0 имеет вид
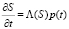 . (5)
. (5)
Делим обе части уравнения (5) на Λ(S) и интегрируем по переменной t:
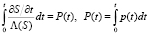 . (6)
. (6)
Используя условие (4), преобразуем интеграл в левой части (6):
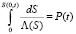 . (7)
. (7)
Формула (7) задает концентрацию осажденных частиц на входе фильтра.
Рассмотрим модель с линейным блокирующим коэффициентом фильтрации:
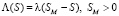 . (8)
. (8)
В этом случае согласно (7) концентрация осадка на входе фильтра
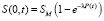 . (9)
. (9)
Согласно [3, 4] для коэффициента фильтрации (8) концентрация осажденных частиц в области 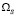 равна
равна
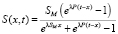 . (10)
. (10)
Расчет полного осадка
Объем осажденных частиц (полный осадок) в пористой среде в момент времени t равен
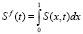 . (11)
. (11)
Если суспензия впрыскивается в пористую среду в течение конечного промежутка времени t1 ≤ t ≤ t2, то Sf(t) = 0 при t ≤ t1. Поскольку частицы проходят от входа до выхода пористой среды за время t0 > 1, то Sf(t) возрастает при t1 < t < t2 + 1 и Sf(t) = Sf(t2 + 1) = const при t > t2 + 1. Если впрыск суспензии происходит при всех значениях времени t > 0, то функция Sf(t) возрастает при t > 0.
Численный расчет выполнен для линейного коэффициента фильтрации (8) при 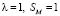 для трех распределений pi(t) концентрации взвешенных частиц на входе фильтра, заданных на рис. 1.
для трех распределений pi(t) концентрации взвешенных частиц на входе фильтра, заданных на рис. 1.
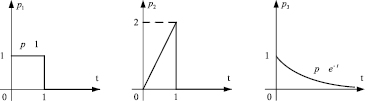
Рис. 1. Концентрации взвешенных частиц на входе фильтра
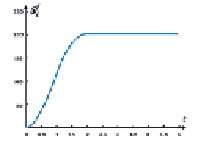
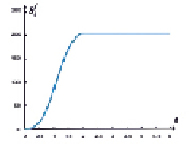
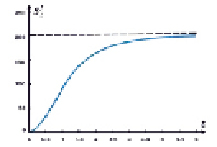
Рис. 2. Полный осадок в пористой среде для трех граничных распределений
На рис. 2 изображены графики полного осадка 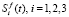 .
.
Общее количество взвешенных частиц, впрыскиваемых в пористую среду, является одинаковым для всех трех рассматриваемых распределений pi(t), поскольку 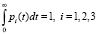 (рис. 1). Для финитных распределений концентрации взвешенных частиц p1(t), p2(t) на входе фильтра полный осадок достигает максимального значения при t = 2; для распределения p3(t) процесс фильтрации длится неограниченно, полный осадок возрастает и стремится к предельному максимальному значению при t → ∞ (рис. 2).
(рис. 1). Для финитных распределений концентрации взвешенных частиц p1(t), p2(t) на входе фильтра полный осадок достигает максимального значения при t = 2; для распределения p3(t) процесс фильтрации длится неограниченно, полный осадок возрастает и стремится к предельному максимальному значению при t → ∞ (рис. 2).
Заключение
В работе рассматривается одномерная математическая модель фильтрации суспензии в однородной пористой среде для переменной концентрации взвешенных частиц на входе фильтра. В случае линейного блокирующего коэффициента фильтрации для решения имеются явные аналитические формулы, обобщающие известное решение для потока суспензии постоянной концентрации. Указанные формулы используются для численного нахождения полного осадка в пористой среде.
Форма распределения концентрации взвешенных частиц на входе фильтра pi(t) определяет вид графика 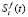 . Поскольку
. Поскольку 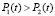 при 0 < t < 1, то на этом интервале график
при 0 < t < 1, то на этом интервале график 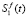 выше графика
выше графика 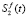 .
.
Согласно рис. 2 предельный полный осадок не зависит от формы распределения концентрации взвешенных частиц на входе фильтра. Величина предельного полного осадка определяется объемом взвешенных частиц, впрыскиваемых в пористую среду.
Найденное точное решение позволит упростить нахождение параметров процесса фильтрации в лабораторных и полевых условиях.



