При кодировании изображений для хранения или передачи с помощью минимального числа бит требуется сохранить качество воспроизводимого изображения в допустимых пределах. Существуют также практические задачи, например связанные с получением, обработкой, передачей и хранением медицинских изображений, в рамках которых необходимо улучшить или восстановить изображение. В любом случае становится актуальным вопрос оценки качества медицинского изображения [1].
Качество изображения можно оценить как количественными (измеримыми), так и качественными (субъективными) показателями. Качественные показатели позволяют значительно упростить выявление того или иного признака, но оперируют более субъективными заключениями, касающимися корреляции и связей. С другой стороны, выявление количественных показателей сопряжено с большими издержками и трудностями, но это окупается точностью полученных данных и меньшими рисками неверной оценки. В данной работе приводится пример оценки качества изображения по разработанной ранее комплексной методике, позволяющей давать субъективную оценку не по общей шкале, как в большинстве других методик, а по нескольким показателям с последующим агрегированием результатов [2].
Для оценки качества изображений предлагается система из семи показателей: резкость, контрастность, яркость, тоновое соответствие, дисторсия и артефакты, шум, разрешение.
По каждому показателю возможны такие варианты оценки как: «очень низкий», «низкий», «средний», «высокий», «очень высокий».
Трактовка понятия «очень низкая резкость», «высокая контрастность», так же как и других понятий, содержащихся в предлагаемых вариантах, у каждого эксперта своя и при этом нечеткая. Поэтому эксперт должен не только выбрать правильный, по его мнению, вариант, но и конкретизировать его количественно. Соотнести с вариантом оценки конкретное число эксперту психологически трудно, так как он не обладает полной информацией о предметной области, и если он это сделает, то может быть допущена грубая ошибка. В связи с этим эксперту предлагается «мягкая» форма количественной интерпретации вариантов оценки: он должен дать не одну, а несколько количественных оценок, соответствующих его пониманию выбранного варианта. Для ориентировки экспертов возможные варианты оценок включаются в анкету [3].
В качестве примера оцениваемого изображения возьмем рентгенограмму легких человека (рисунок), которая была заранее искусственно искажена с помощью применения фильтра размытия по Гауссу и алгоритма сжатия jpg для имитации искажений, возникающих при получении, обработке и передаче подобных изображений [4].
В рассматриваемом случае множество возможных оценок будет иметь вид {5 %, 20 %, 35 %, 50 %, 65 %, 80 %, 95 %} (интервал от 0 % до 100 % поделен на равные части). Так, если эксперт считает, что резкость, равная 5 %, 20 %, 35 %, является очень низкой, то он должен выбрать соответствующий вариант оценки (табл. 1). Кроме того, он должен присвоить каждой оценке степень уверенности в том, что именно она будет иметь место.
Таблица 1
Пример заполненного экспертом фрагмента анкеты
|
Вариант оценки |
Возможные значения уровня резкости, % |
||||||
|
5 |
20 |
35 |
50 |
65 |
80 |
95 |
|
|
Очень низкая |
|||||||
|
Низкая |
|||||||
|
Средняя |
|||||||
|
Высокая |
0,4 |
0,9 |
1,0 |
0,8 |
0,5 |
0,0 |
0,0 |
|
Очень высокая |
|||||||
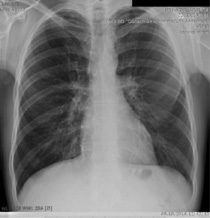
Рентгенограмма легких человека
Чтобы избежать опасности навязывания эксперту вариантов оценки, ему может быть предоставлена возможность выхода за пределы предлагаемого множества оценок.
Пример заполнения анкеты представлен в табл. 1.
Такое заполнение анкеты говорит о том, что эксперт, выбрав вариант «высокая», имеет в виду следующее:
– скорее всего, уровень резкости изображения составляет 35 %;
– возможно, что он составляет и 20 %/50 %, но утверждать это можно с несколько меньшей уверенностью (0,9/0,8);
– маловероятно (0,5/0,4), но он может составлять 65 %/5 %;
– степень уверенности в том, что данный показатель примет другие значения, равна 0.
Для удобства дальнейшего анализа результаты опроса пяти экспертов по каждому i-му показателю целесообразно свести в таблицы. Пример для одного из показателей представлен в табл. 2.
Таблица 2
Пример оценки показателя группой экспертов
|
№ эксперта |
Возможные значения резкости, % |
||||||
|
5 |
20 |
35 |
50 |
65 |
80 |
95 |
|
|
1 |
0,4 |
0,9 |
1,0 |
0,8 |
0,5 |
0,0 |
0,0 |
|
2 |
0,0 |
0,0 |
0,5 |
1,0 |
0,4 |
0,0 |
0,0 |
|
3 |
0,3 |
0,8 |
1,0 |
0,9 |
0,8 |
0,6 |
0,0 |
|
4 |
0,0 |
0,5 |
1,0 |
0,9 |
0,5 |
0,0 |
0,0 |
|
5 |
0,0 |
0,4 |
0,5 |
1,0 |
0,8 |
0,6 |
0,0 |
Если уровень компетентности всех экспертов одинаков, то обобщенная нечеткая оценка в самом простом варианте может быть получена как пересечение нечетких множеств, соответствующих индивидуальным оценкам экспертов.
Однако сформировать однородную группу экспертов практически невозможно, более того, однородная группа далеко не всегда обеспечивает необходимый уровень объективности результатов экспертизы: результаты опроса такой группы могут оказаться смещенными. Более рациональным является подход, при котором предусматривается возможность выявления мнения каждого эксперта – уникального носителя экспертных знаний. В этой связи актуальной является задача оценки согласованного мнения экспертов.
Для расчета построим сводную матрицу индивидуальных экспертных оценок семи показателей (f1 – f7) (табл. 3).
Таблица 3
Сводная матрица индивидуальных экспертных оценок
|
№ эксперта |
Показатели |
||||||
|
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
|
1 |
[0.4, 0.9, 1.0, 0.8, 0.5, 0.0, 0.0] |
[0.0, 0.3, 0.8, 1.0, 0.8, 0.0, 0.0] |
[0.0, 0.4, 0.6, 1.0, 0.4, 0.0, 0.0] |
[0.2, 0.3, 0.4, 1.0, 0.6, 0.5, 0.0] |
[0.0, 0.5, 0.8, 1.0, 0.5, 0.0, 0.0] |
[0.0, 0.3, 0.7, 1.0, 0.4, 0.0, 0.0] |
[0.5, 0.6, 1.0, 0.9, 0.6, 0.0, 0.0] |
|
2 |
[0.0, 0.0, 0.5, 1.0, 0.4, 0.0, 0.0] |
[0.3, 0.8, 1.0, 0.4, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.4, 1.0, 0.8, 0.2, 0.0] |
[0.0, 0.8, 1.0, 0.7, 0.5, 0.0, 0.0] |
[0.0, 0.0, 0.6, 1.0, 0.7, 0.0, 0.0] |
[0.0, 0.6, 1.0, 0.8, 0.7, 0.6, 0.2] |
[0.3, 0.4, 1.0, 0.4, 0.0, 0.0, 0.0] |
|
3 |
[0.3, 0.8, 1.0, 0.9, 0.8, 0.6, 0.0] |
[0.0, 0.5, 1.0, 0.4, 0.0, 0.0, 0.0] |
[0.0, 0.7, 1.0, 0.7, 0.3, 0.0, 0.0] |
[0.0, 0.7, 1.0, 0.5, 0.2, 0.0, 0.0] |
[0.0, 0.0, 0.9, 1.0, 0.5, 0.0, 0.0] |
[0.5, 0.9, 1.0, 0.7, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.8, 1.0, 0.6, 0.0, 0.0] |
|
4 |
[0.0, 0.5, 1.0, 0.9, 0.5, 0.0, 0.0] |
[0.1, 0.4, 1.0, 0.6, 0.2, 0.0, 0.0] |
[0.0, 0.6, 1.0, 0.6, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.6, 1.0, 0.4, 0.0, 0.0] |
[0.0, 0.0, 0.4, 1.0, 0.6, 0.2, 0.0] |
[0.0, 0.0, 0.4, 1.0, 0.8, 0.0, 0.0] |
[0.0, 0.7, 0.9, 1.0, 0.4, 0.0, 0.0] |
|
5 |
[0.0, 0.4, 0.5, 1.0, 0.8, 0.6, 0.0] |
[0.0, 0.3, 0.8, 1.0, 0.9, 0.7, 0.0] |
[0.0, 0.2, 0.8, 1.0, 0.9, 0.4, 0.2] |
[0.4, 0.6, 1.0, 0.5, 0.0, 0.0, 0.0] |
[0.6, 0.8, 0.9, 1.0, 0.7, 0.5, 0.0] |
[0.0, 0.0, 0.6, 1.0, 0.8, 0.0, 0.0] |
[0.0, 0.0, 0.8, 1.0, 0.4, 0.0, 0.0] |
Элементы матрицы представляют собой оценку k-м экспертом показателя fi. Естественно, эти оценки в большинстве своем не будут совпадать.
Векторы групповой оценки pt и весовых коэффициентов компетентности vt рассчитываются по итеративным:
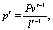 (1)
(1)
где lt – нормирующий коэффициент, рассчитывающийся по формуле
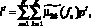 (2)
(2)
где N – количество оцениваемых КПЭ.
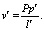 (3)
(3)
Вычислительный процесс продолжается до тех пор, пока различия в значениях весовых коэффициентов не будут превышать заданной перед началом проведения опроса величины.
Обычно достаточно выполнить две-три итерации, чтобы с точностью до тысячных долей единицы оценить вектор групповой оценки и вектор весовых коэффициентов компетентности.
В ходе вычислений по формулам (1)–(3) были получены следующие весовые коэффициенты компетентности пяти экспертов: 0,213; 0,184; 0,201; 0,173; 0228.
Выявить экспертов, имеющих мнение, резко отличающееся от мнения других экспертов, можно с помощью корреляционного анализа. Разумеется, эксперт имеет право на собственное мнение, отличное от мнения других экспертов. Однако следует признать, что более реалистичной является та точка зрения, что оценка компетентности эксперта тем выше, чем меньше отличие его оценки от групповой. С учетом данного предположения можно отбросить мнение экспертов, имеющих наибольшее отличие от групповой оценки.
Влияние уровня компетентности эксперта на нечеткую количественную меру μk(fi) предлагается реализовать путем выполнения операции «размывание». Математическое «размывание» нечеткой количественной меры μk(fi) реализуется путем возведения ее в степень, соответствующую коэффициенту компетентности эксперта (табл. 4).
Таблица 4
Матрица индивидуальных экспертных оценок с учетом компетентности экспертов
|
№ эксперта |
Показатели |
||||||
|
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
|
1 |
[0.8, 1.0, 1.0, 1.0, 0.9, 0.0, 0.0] |
[0.0, 0.8, 1.0, 1.0, 1.0, 0.0, 0.0] |
[0.0, 0.8, 0.9, 1.0, 0.8, 0.0, 0.0] |
[0.7, 0.8, 0.8, 1.0, 0.9, 0.9, 0.0] |
[0.0, 0.9, 1.0, 1.0, 0.9, 0.0, 0.0] |
[0.0, 0.8, 0.9, 1.0, 0.8, 0.0, 0.0] |
[0.9, 0.9, 1.0, 1.0, 0.9, 0.0, 0.0] |
|
2 |
[0.0, 0.0, 0.9, 1.0, 0.8, 0.0, 0.0] |
[0.8, 1.0, 1.0, 0.8, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.8, 1.0, 1.0, 0.7, 0.0] |
[0.0, 1.0, 1.0, 0.9, 0.9, 0.0, 0.0] |
[0.0, 0.0, 0.9, 1.0, 0.9, 0.0, 0.0] |
[0.0, 0.9, 1.0, 1.0, 0.9, 0.9, 0.7] |
[0.8, 0.8, 1.0, 0.8, 0.0, 0.0, 0.0] |
|
3 |
[0.8, 1.0, 1.0, 1.0, 1.0, 0.9, 0.0] |
[0.0, 0.9, 1.0, 0.8, 0.0, 0.0, 0.0] |
[0.0, 0.9, 1.0, 0.9, 0.8, 0.0, 0.0] |
[0.0, 0.9, 1.0, 0.9, 0.7, 0.0, 0.0] |
[0.0, 0.0, 1.0, 1.0, 0.9, 0.0, 0.0] |
[0.9, 1.0, 1.0, 0.9, 0.0, 0.0, 0.0] |
[0.0, 0.0, 1.0, 1.0, 0.9, 0.0, 0.0] |
|
4 |
[0.0, 0.9, 1.0, 1.0, 0.9, 0.0, 0.0] |
[0.7, 0.9, 1.0, 0.9, 0.8, 0.0, 0.0] |
[0.0, 0.9, 1.0, 0.9, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.9, 1.0, 0.9, 0.0, 0.0] |
[0.0, 0.0, 0.9, 1.0, 0.9, 0.8, 0.0] |
[0.0, 0.0, 0.9, 1.0, 1.0, 0.0, 0.0] |
[0.0, 0.9, 1.0, 1.0, 0.9, 0.0, 0.0] |
|
5 |
[0.0, 0.8, 0.9, 1.0, 1.0, 0.9, 0.0] |
[0.0, 0.8, 1.0, 1.0, 1.0, 0.9, 0.0] |
[0.0, 0.7, 1.0, 1.0, 1.0, 0.8, 0.7] |
[0.8, 0.9, 1.0, 0.9, 0.0, 0.0, 0.0] |
[0.9, 1.0, 1.0, 1.0, 0.9, 0.9, 0.0] |
[0.0, 0.0, 0.9, 1.0, 1.0, 0.0, 0.0] |
[0.0, 0.0, 1.0, 1.0, 0.8, 0.0, 0.0] |
В результате опроса множества всех экспертов (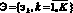 ) для каждого i-го (
) для каждого i-го (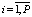 ) показателя имеем K нечетких количественных мер
) показателя имеем K нечетких количественных мер 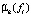 , учитывающих степени компетентности опрашиваемых экспертов. Нечеткое множество, характеризующее обобщенное мнение группы, определяется в соответствии с правилом выполнения операции пересечения нечетких множеств [5] (табл. 5).
, учитывающих степени компетентности опрашиваемых экспертов. Нечеткое множество, характеризующее обобщенное мнение группы, определяется в соответствии с правилом выполнения операции пересечения нечетких множеств [5] (табл. 5).
Таблица 5
Обобщенное мнение экспертной группы
|
Показатели |
||||||
|
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
[0.0, 0.0, 0.9, 1.0, 0.8, 0.0, 0.0] |
[0.0, 0.8, 1.0, 0.8, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.8, 0.9, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.8, 0.9, 0.0, 0.0, 0.0] |
[0.0, 0.0, 0.9, 1.0, 0.9, 0.0, 0.0] |
[0.0, 0.0, 0.9, 0.9, 0.0, 0.0, 0.0] |
[0.0, 0.0, 1.0, 0.8, 0.0, 0.0, 0.0] |
Полученные в ходе экспертного оценивания показатели влияют на оценку качества изображения в различной степени. Таким образом, большое значение здесь имеют весовые коэффициенты. Эти коэффициенты также определяются экспертной оценкой. Наиболее целесообразно использовать здесь метод парных сравнений, в котором экспертам предлагается произвести сравнение показателей эффективности попарно с тем, чтобы установить в каждой паре наиболее важный (значимый) [6].
Для этого составляют матрицы парных сравнений, в которых все показатели (1, 2, …, M) записываются в одном и том же порядке дважды: в верхней строке и в первом столбце. Каждый эксперт должен проставить на пересечении строки и столбца для двух сравниваемых показателей оценку aij, которая показывает, во сколько раз i-й показатель имеет большую степень влияния, чем j-й показатель (табл. 6).
Таблица 6
Матрица парных сравнений для одного из экспертов
|
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
|
|
f1 |
1 |
4 |
6 |
9 |
5 |
7 |
5 |
|
f2 |
4 |
1 |
4 |
4 |
7 |
2 |
7 |
|
f3 |
6 |
4 |
1 |
6 |
5 |
4 |
4 |
|
f4 |
9 |
4 |
6 |
1 |
9 |
1 |
5 |
|
f5 |
5 |
7 |
5 |
9 |
1 |
3 |
9 |
|
f6 |
7 |
2 |
4 |
1 |
3 |
1 |
6 |
|
f7 |
5 |
7 |
4 |
5 |
9 |
6 |
1 |
На основе значений полученного собственного столбца матрицы определяют приоритеты (значимость или важность) показателей [1].
После этого мнения экспертов необходимо агрегировать с учетом их компетентности. В результате были получены следующие значения весовых коэффициентов показателей: 0,121; 0,086; 0,106; 0,126; 0,216; 0,145; 0,199.
Для количественного выражения качества изображения с помощью N показателей, необходимо воспользоваться аддитивной моделью (табл. 7).
Таблица 7
Значение качества изображения, представленное в нечеткой форме
|
Возможные значения качества, % |
||||||
|
5 |
20 |
35 |
50 |
65 |
80 |
95 |
|
0,0 |
0,1 |
0,7 |
0,8 |
0,4 |
0,0 |
0,0 |
Для получения однозначного количественного значения обычно выбирают тот элемент f*, который имеет максимальную степень принадлежности к полученному обобщенному нечеткому множеству мнений экспертной группы. В данном случае – 50 %. Это значение и будет искомой оценкой качества изображения.
Таким образом, был проведен расчет значения качества изображения по разработанной ранее методике комплексной субъективной оценки качества изображения по нескольким показателям.
Важной особенностью подхода является использование нечетких чисел, обусловленное тем, что не всегда удается получить корректные показатели в точном количественном выражении, а намного удобнее использовать нечеткие значения этих показателей, особенно если речь идет об экспертном опросе.
Также преимуществами предлагаемой методики являются универсальность и гибкость. Данная методика не привязывается к конкретным изображениям, а может быть адаптирована к любому типу изображений, например к медицинским: снимки УЗИ, рентгенограммы, флюорограммы, томограммы и т.д. С помощью нее можно, например, оценить возможность и эффективность дальнейшего применения к изображению алгоритмов оконтуривания, сегментации и распознавания, что является одним из направлений автоматизации процессов диагностирования патологий [7].
На основе предложенного алгоритма впоследствии может быть разработана автоматизированная информационная система оценки качества, упрощающая процедуру проведения экспертного опроса и обработку результатов исследования.



