Использование тонкодисперсных порошков оксидов металлов при получении керамических композиционных материалов позволяет синтезировать изделия различного назначения с уникальными прочностными свойствами, создавать конструкционные металлозамещающие материалы, защитные покрытия, а также фильтры, мембраны, теплоизоляционные и каталитические структуры с заданным размером пор. Одной из перспективных технологий получения керамических порошков с контролируемыми параметрами является плазмохимический синтез, включающий термохимическое разложение жидкокапельных реагентов (прекурсоров) в потоке высокотемпературного газообразного теплоносителя [2, 4, 5]. Структура и форма керамических частиц, получаемых плазмохимическим методом, является важнейшим параметром, определяющим качество целевого продукта. Для получения частиц с заданными характеристиками необходимо выбрать соответствующий режим работы плазмохимического реактора.
Процесс плазмохимического синтеза керамических порошков является многофакторным и многостадийным. Обычно рассматриваются следующие составляющие: распыливание жидкого прекурсора с образованием полидисперсных капель в объеме реактора, тепломассообмен движущихся капель с потоком высокотемпературного теплоносителя, нагрев и испарение жидких частиц, сопровождающиеся внутрикапельной диффузией и выпадением солевого осадка; термолиз соли и ее спекание с образованием твердой частицы определенной морфологии.
Анализ отдельных стадий плазмохимического синтеза, данный в работах [7, 9], показал, что формирование морфологии частиц порошка происходит на стадии испарения капли. При этом процесс испарения растворителя предопределяет реализацию максимальной концентрации соли С на поверхности капли, в то время как процесс диффузии ведет к выравниванию С по объему жидкой частицы. Можно предположить, что при достижении концентрации соли в растворе некоторого критического значения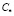 
происходит выпадение солевого остатка в той части объема (приповерхностного слоя) капли, где 
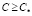. При этом в зависимости от скорости испарения растворителя и скорости диффузии соли возможны два варианта формообразования – при интенсивном испарении выпадение солевого остатка начинается достаточно быстро и растворенная соль образует полую сферическую структуру частицы. При относительно медленном выпаривании растворителя процесс диффузии успевает переносить растворенную соль к центру капли, что приводит к формированию ядра сплошного типа.
Для коэффициента диффузии D характерное время данного процесса в объеме капли определяется соотношением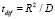 
. Характерное время испарения жидкости с поверхности капли радиуса R можно оценить из модели приведенной пленки [3]:
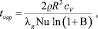
где – число Сполдинга; – число Нуссельта;
λg – коэффициент теплопроводности газа при температуре кипения;
ρ – плотность газа;
сV – удельная теплоемкость паров растворителя при постоянном объеме.
Основными параметрами процесса, определяющими структуру конечного продукта, являются характеристики режима работы реактора (скорость капель, время их пребывания в реакторе, температура теплоносителя), а также соотношение K отношения характерных времен внутрикапельной диффузии tdif испарения tvap
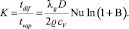
Можно отметить, что параметр K не зависит от радиуса капли R.
В работах [5, 7, 9] показано, что при движении капли прекурсора в потоке теплоносителя температура жидкой частицы достаточно быстро повышается до уровня начала испарения растворителя с ее поверхности, а профиль температуры становится практически равномерным. В дальнейшем концентрация растворенной соли вблизи поверхности капли повышается, соль диффундирует к центру капли и при достижении определенного значения концентрации происходит образование конденсированного осадка.
Скорость u изменения радиуса R капли за счет испарения растворителя можно определить соотношением [1, 9]:
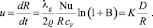(1)
После того как температура поверхности капли прекурсора достигла температуры равновесного испарения (кипения), радиус частицы R начинает уменьшаться. Далее считается, что температура поверхности капли остается постоянной и равной температуре равновесного испарения. Вследствие выпаривания растворителя концентрация соли C у поверхности повышается и начинается процесс диффузии, который описывается уравнением
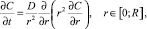(2)
где r – координата, направленная от центра капли.
Начальным условием (момент времени t = 0) для уравнения (2) является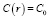 
.
Граничные условия в центре капли
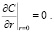(3)
Граничные условия на поверхности капли в режиме испарения растворителя
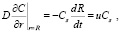(4)
где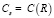 
– концентрация на поверхности жидкой частицы.
Используя аналогию тепловых и диффузионных процессов для решения уравнения (2), можно использовать метод интегрального (в данном случае массового) баланса [6, 8], предполагающего для рассматриваемых условий следующий профиль концентрации по зоне наличия градиента толщиной δ (рис. 1, a):
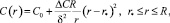
где
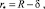
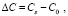(5)
где δ – толщина градиентной зоны концентрации.
Интегрируя уравнение (2) по координате r
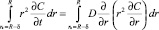
с учетом зависимости (5) в пределах переменных радиуса R капли и длины δ градиентной зоны по правилу Лейбница, получим
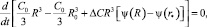
где
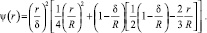
Интегрируя полученное обыкновенное дифференциальное уравнение по времени, можно получить конечное соотношение, связывающее концентрацию на поверхности капли с размером градиентной зоны:
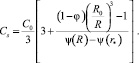(6)
Другую связь между Cs и δ можно получить из дифференцирования профиля температуры (5), граничных условий (4) с учетом соотношения (1)
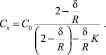(7)
Таким образом, из соотношений (6) и (7) для любого текущего радиуса капли R можно определить концентрацию Cs на поверхности и толщину градиентного слоя δ при выполнении условия R ≥δ
В случае, когда возмущение концентрации достигло цента капли, то вместо профиля можно использовать [8] зависимость (рис. 1, б)
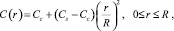
где Cс – концентрация в центре жидкой частицы.
После аналогичных вышеописанным преобразований для данного случая можно получить обыкновенное дифференциальное уравнение
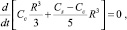
решая которое, концентрацию Cс в центре жидкой частицы и на поверхности капли Cs можно определить явно:
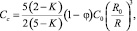
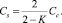(8)
Параметр φ, входящий в уравнения (6) и (8), задает долю (от начальной) солевой массы, выпадающей в осадок.
Алгоритм определения параметров распределения концентрации в капле и доли выпавшей в осадок соли следующий.
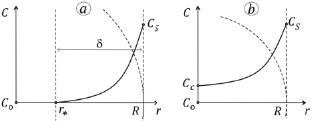
Рис. 1. Схема области решения
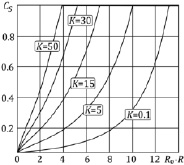
Рис. 2. Зависимость концентрации Cs от уровня выпаривания
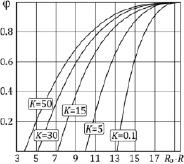
Рис. 3. Зависимость массовой доли выпадающего солевого осадка от уровня выпаривания
1. По теплофизическим свойствам материалов и геометрическим характеристикам реактора по усредненным параметрам течения теплоносителя из формулы (1) определяется безразмерный критерий K – соотношение характерных времен испарения и диффузии, скорость испарения u, время нахождения жидкой частицы в камере реактора и радиус R частицы на выходе из реактора.
2. Для φ = 0 по соотношениям (6), (7) или (8) рассчитывается концентрация Cs на поверхности капли.
3. Eсли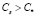 
(
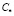– равновесная концентрация, при которой начинается солеобразование), то выбирается такое значение параметра φ, при котором 
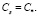Таким образом, для жидкокапельной частицы на выходе из реактора будут определены все ее характеристики, включая координаты области выпадения солевого остатка.
В качестве примера рассматривается эволюция капли радиуса R0 = 20 мкм слабоконцентрированного (C0 = 0,04) водного раствора соли при диффузии с коэффициентом D = 2•10–9 м2/с и условному значению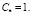 
На рис. 2 для различных значений критерия K даны зависимости концентрации Cs от уровня выпаривания R0 – R. Видно, что, чем выше значение K, тем быстрее концентрация на поверхности достигает равновесного значения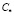 
, определяющего начало процесса выпадения солевого остатка. На рис. 3 представлены зависимости массовой доли выпадающего солевого осадка φ от уровня выпаривания для различных значений критерия K. Данные соответствуют развитию физического процесса, представленного на рис. 2, и дают представление о размере и положении области (по пространству частицы) выпадения солевого остатка. Для локализации 80 %-го выпадения массы соли на рис. 4 приведена диаграмма, характеризующая область конденсата после выпаривания растворителя прекурсора.
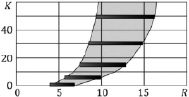
Рис. 4. Локализации 80 %-го выпадения массы соли для частицы исходного размера в 20 мкм
Таким образом, в работе представлен алгоритм аналитической оценки параметров формообразования частиц в плазмохимическом реакторе, базирующийся на решении задачи диффузии во внутрикапельном пространстве прекурсора при выпаривании растворителя. Предложенный подход позволяет определить массовую долю и локализацию выпадающего солевого осадка для различных уровней глубины выпаривания.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-38-60031 мол_а_дк».