Будем рассматривать распространение примеси в ходе физических процессов, протекающих в верхнем слое открытого океана под воздействием атмосферы. При этом образующиеся в воде возмущения имеют масштабы T0 = 105 c, L0 = 103 м, Н0 = 102 м и вызваны синоптическими атмосферными явлениями протяженностью 100–1000 км. Таким характеристикам соответствуют чуть ли не все среднемасштабные процессы: микроструктура, дрейфовые и приливные течения, инерционные колебания и атмосферные синоптические процессы.
Все эти процессы имеют турбулентный характер. Поэтому при их исследовании будем использовать физико-математическую модель, описывающую изменения вертикального распределения средних значений характеристик стратифицированной среды и параметров мелкомасштабной турбулентности в приближении горизонтальной однородности нелинейной системой одномерных дифференциальных уравнений гидродинамики, записанных без учета адвекции и горизонтального турбулентного обмена в виде [1]:
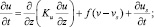 (1)
(1)
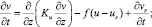 (2)
(2)
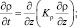 (3)
(3)
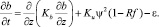 (4)
(4)
Модель дополнена уравнением диффузии примеси:
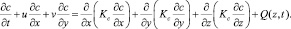 (5)
(5)
Здесь 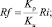
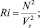
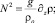
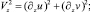
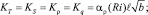
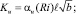
u, v – компоненты вектора скорости; T – температура; S – соленость; ρ – плотность; b – энергия турбулентности; с – концентрация примеси; Q – функция источников; Ki – кинематические коэффициенты турбулентного обмена (i = u, T, S, b, ρ, q), КL = 0,1l см2/с.
Модель замыкается полуэмпирическими гипотезами для расчета масштаба турбулентности l и функций αi(Ri) [1]:
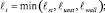
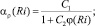
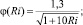
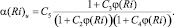
Масштабы l st, l unst, l wall для устойчивой, неустойчивой стратификации и вблизи твердой границы вычисляются по модифицированным гипотезам Лозоватского – Озмидова, Блакадара и Кармана.
Скорость вязкой диссипации определяется из гипотезы Колмогорова
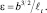
Для других коэффициентов турбулентного обмена примем Kc = Kρ и Kb = cbKu. Из-за отсутствия данных наблюдений для отношения Kb/Ku = cb примем, что cb = 0,73.
Краевая задача решается при следующих начальных и граничных условиях:
t = 0; u = uo(z); v = vo(z); ρ = ρo(z); с = сo(z); b = bo(z);
z = 0; 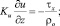
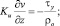
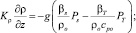
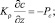
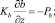
z = H; u = v = 0; с = сH;
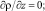
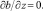
Здесь τx, τy – составляющие касательного напряжения ветра на верхней границе водоема; PT, Ps, Pq, Pb – потоки тепла, соли, пассивной примеси и энергии турбулентности из атмосферы в водную среду; ρo, сpo – характерное значение плотности и удельная теплоемкость жидкой среды; βT, βs – коэффициенты термического расширения и соленостного сжатия морской воды; H – глубина водоема. Для решения нестационарной задачи все потоки на верхней границе рассчитываются по стандартным методикам, а для потока примеси при z = 0 принимается Pq = 0.
Задача решалась численно конечно-разностными методами [2]. При аппроксимации дифференциальных уравнений конечно-разностными аналогами использовался бокс-метод на сдвинутых сетках. По временной координате применялась абсолютно устойчивая схема Кранка – Николсона второго порядка точности. Вследствие этого пространственно-временные шаги выбирались только из соображений адекватного описания мелкомасштабной турбулентности и составляли Δz = 20 см, Δt = 3 мин.
Поставленная задача решалась для шельфовой зоны окраинных морей в районе Байдарацкой губы Карского моря. Составляющие us, vs скорости приливного течения для данной местности рассчитываются по формулам полусуточных приливов:
us = uo sin(2π (t – tu)/T1);
vs = vo sin(2π (t – tv)/T1)
с периодом T1 = 12,42 часа при uo = 0,3 м/с, vo = 0,4 м/с, tu = 3 ч, tv = –2 ч.
Расчеты выполнялись для условий, соответствующих концу летнего прогрева. Метеорологическая ситуация совпала с прохождением небольшого шторма с недолгим усилением ветра от 6,3 до 20 м/с. Рис. 1 демонстрирует результаты этих расчетов. Серия расcчитанных профилей плотности начинается с 10 часов дня. Этот период связан с развитием однородности в верхнем и нижнем погранслоях. В дневное время суток при усилении ветра и отрицательном потоке плавучести за счет турбулентности, генерируемой сдвигом средней скорости течения, толщины верхнего и нижнего погранслоев развились до 8 и 5 м соответственно. К концу суток вследствие конвективно-ветрового перемешивания нижняя граница верхнего перемешанного слоя достигла 10 м, а верхняя граница нижнего перемешанного слоя залегала примерно на уровне 13 м. Это вызвало почти полное смыкание перемешанных слоев с вырождением пикноклина в прослойку скачка плотности толщиной приблизительно 3–5 м, то есть привело к образованию трехслойной структуры. Последовавшее ослабление ветра вызвало в обоих слоях инерционные колебания с периодом ~13 час. Для поля плотности это выразилось в вертикальных смещениях границы раздела перемешанных слоев с амплитудой около 5 м. В периоды экстремального залегания граница обостряется, а при смещениях, вследствие вовлечения жидкости из соседнего слоя и ее перемешивания, размывается, плотность верхнего слоя уменьшается, а нижнего растет [3].
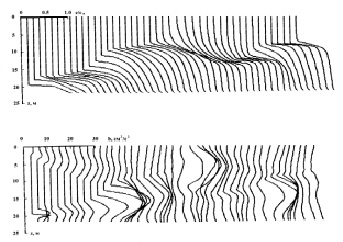
Рис. 1. Профили вертикального распределения пассивной примеси и энергии турбулентности с интервалом 2 часа
Рис. 1 (внизу) показывает эволюцию вертикальных распределений энергии турбулентности во время шторма и после него. Характерным для начального периода является наличие максимума энергии турбулентности в нижней части ВПС и верхней НПС (первые два профиля на рис. 1), связанного с высокими градиентами скорости в этих зонах. Уровень турбулентности в каждом слое во время шторма одного порядка, а более позднее периодическое затухание вызвано изменениями сочетания приливной и дрейфовой скорости. В связи с этим следует отметить периодическое сужение одной области, охваченной турбулентностью, за счет другой, чем и объясняется эффект вертикальных колебаний границы раздела двух перемешанных слоев. Турбулентность носит циклический характер, весьма многообразна по форме вертикального распределения и в зависимости от фазы может иметь яркий максимум около центра ПС, либо быть однородной по всему слою, либо монотонно возрастать от границы раздела перемешанных слоев.
Рассмотрено распространение примеси от источника, расположенного на дне водоема в зоне действия приливного течения. Вертикальные профили концентрации примеси с(z) приведены на рис. 1 (вверху). Их также отличает достаточно высокая однородность внутри НПС и резкое уменьшение внутри слоя скачка плотности. При смыкании верхнего и нижнего турбулентных слоев, как это произошло в ходе моделируемого шторма, наблюдается постепенное вовлечение примеси через границу раздела и ее турбулентная диффузия внутри ВПС. После двух суток такого перемешивания концентрация примеси в верхнем слое составила около 15 % от ее характерных значений у дна. Основной вынос примеси из придонного слоя в ВПС происходит в период инерционного смещения границы раздела слоев вниз за счет вовлечения насыщенной примесью жидкости нижнего слоя. Затем турбулентное перемешивание в верхнем слое выравнивает концентрацию.
Предложенная модель описывает вентиляцию придонного слоя в одномерной модели вследствие выноса примеси через поверхность скачка плотности посредством турбулентного вовлечения. Инерционные колебания в поле скорости движения среды приводят к периодическим обострениям вертикальных градиентов скорости и локальному усилению турбулентности. Вследствие этого на границе раздела слоев активизируется вовлечение среды другого слоя вместе с субстанцией, то есть ее внос через границу раздела слоев. Сразу же турбулентное перемешивание разносит примесь по всему слою. В другом расчете источник примеси постоянной мощности находится у поверхности, на которую действует ветер со скоростью 6 м/с. Плотность в среде имеет линейное распределение. Под действием ветра образуется дрейфовое течение, перемешивающее воду от поверхности вглубь водоема.
Первые двое суток происходит процесс вовлечения ламинарной среды нижнего слоя в верхний хорошо перемешанный турбулентный слой. Граница раздела слоев с некоторым замедлением смещается вниз, претерпевая периодические изменения в своей структуре с инерционным периодом [5]. После двух суток режим перемешивания в слое изменился. На нижней границе однородного слоя возникла ступенчатая микроструктура. Такие неоднородности в поле плотности известны для энергоактивных зон, теоретически описаны Краненбургом и экспериментально изучены Лиу [4].
На рис. 2 приведена картина вертикального распределения примеси за тот же период. Источник постоянной мощности генерирует однородную мелкодисперсную нетяжелую примесь (например, краситель), которая турбулентностью практически равномерно перераспределяется по перемешанному слою. В области скачка плотности распределение примеси имеет сложную структуру, которая со временем претерпевает трансформацию. Наблюдаются три периода в формировании вертикального распределения примеси. В период активного вовлечения (первые 0,25 сут) профили c(z) не имеют перегибов и примесь быстро распространяется вниз за счет вовлечения чистой ламинарной жидкости из нижнего слоя. Второму периоду (дальнейшие 1,5 сут) свойственно распределение концентрации с перегибами линии c(z) и с изменением формы профиля с инерционным периодом. В профиле возникают зачатки ступенчатой структуры, которые быстро диссипируют (верхний рисунок). Третий период демонстрирует стадию эволюции сформировавшейся ступенчатой структуры (нижний рисунок), когда ступени существуют на протяжении нескольких часов, прежде чем поглощаются другими ступенями.
На рис. 3 приведен осевой разрез сформировавшегося пятна примеси от точечного источника, расположенного на поверхности. Шлейф примеси имеет сложную структуру, образованную цепочкой областей повышенной концентрации.
Более того, зоны повышенной концентрации также неравноценны: между пятнами с высокой концентрацией обнаруживаются 2–3 пятна концентрации меньшего уровня. Пятна прослеживаются до глубины, составляющей 2/3 толщины перемешанного слоя.
Такое распределение примеси в верхнем слое водоема при коэффициентах вертикальной диффузии, рассчитываемых по данной методике, получено впервые, хотя образования микроструктуры примеси можно было бы ожидать по виду поля плотности, как из экспедиционных наблюдений, так и из численных экспериментов.

Рис. 2. Профили вертикального распределения примеси с интервалом в 1 час
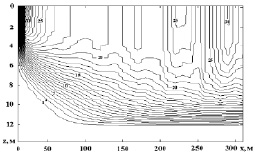
Рис 3. Вертикальный осевой разрез пятна примеси от неподвижного точечного источника на поверхности
В итоге изучены основные закономерности формирования полей пассивной примеси в среде, находящейся под различными внешними воздействиями. Проведено сравнение расчетов с реальной геофизической ситуацией и сделаны выводы о возможности применения модели к решению такого класса задач. Изучено распространение примеси в шельфовой зоне от источника, расположенного на дне. В ходе расчетов обнаружен и описан случай выноса примеси через слой скачка плотности – слой инверсии из придонного турбулентного слоя во внешнюю среду. Проведено моделирование формирования ступенчатой структуры полей плотности и примеси в стратифицированной среде. Исследована зависимость распространения трехмерного пятна примеси в водной среде от точечного источника. Установлено, что при слабой адвекции среды шлейф примеси имеет плавное изменение от точки вноса примеси к периферии, а при скорости движении среды в десятки сантиметров в структуре шлейфа образуются области (пятна) повышенной концентрации примеси. Приводятся примеры аналогичных распределений в реальных опытах. Сделан вывод, что модель может применяться для прогноза распространения примеси и расчетов изменения вертикальной термической, динамической и плотностной структуры пограничных слоев атмосферы и океана, в том числе структуры верхнего слоя океана по данным метеорологических наблюдений. Результаты расчетов распространения примеси могут служить объяснением уже известных данных наблюдений и являться обоснованием новых экспериментальных программ. Помимо этого, модель может быть использована в задачах, связанных с изучением образования и эволюции тонкой или ступенчатой структуры полей плотности и примеси.



