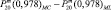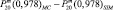Строгое решение задачи рассеяния электромагнитной волны на вращающейся диэлектрической сфере, было получено в работе [6]. Окончательные выражения для внутренних и внешних полей были получены с использованием сферических гармоник. Решение для неподвижной сферы полностью совпадает с теорией Ми [5], поля, вызванные вращением рассеивателя, находятся решением уравнений Максвелла для реконструированной среды распространения и граничных условий, учитывающих поверхностный ток [6, 7, 8]. Однако подобный подход не является единственным. Данную задачу можно решить, используя тензорные функции Грина [3], опять же применяя постоянную распространения в реконструированной среде. Оба этих подхода в результате дают аналитическое решение поставленной задачи, однако применение подобного аппарата для широкого спектра систем, начальное состояние которых может изменяться в значительном диапазоне, оказывается затруднительным. В работе [2] описываются параметры вычислительного эксперимента двухмерной дифракционной задачи рассеяния на слабопроводящем цилиндре.
Цель данного исследования - проследить и оценить погрешности, вносимые в аналитические расчеты при симулировании физической системы. Важным в этом контексте, является максимально широкий диапазон допустимых начальных условий, таких как частота падающей волны (f), диэлектрическая и магнитная проницаемость сферы (ε, μ), положение источника в пространстве, угловая скорость вращения рассеивателя (Ω) и т.д. Там, где это возможно и необходимо, был реализован собственный алгоритм аналитического расчета, который является приоритетным перед численными методами.
Постановка задачи
Подобно тому как разложение экспоненты для плоской ЭМВ, e-ikx, где k – волновое число x – координата прямоугольной системы, по цилиндрическим функциям, является ключевым для решения двухмерной задачи дифракции на цилиндре, похожая процедура (1) по сферическим функциям является отправной точкой для решения трехмерной задачи рассеяния на сфере [6]:
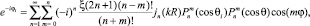(1)
где ξ = 1, при m = 0 и ξ = 2 для всех прочих значений. Сферические функции, входящие в разложение: jn(kR) – сферические функции Бесселя и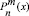 
– присоединенные функции Лежандра. (R, θ,φ) – координаты сферической системы, а индекс «i» применяется к величинам, относящимся к источнику ЭМВ. Угол фазы в сферических координатах определяется соотношением:
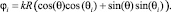(2)
Задача решается с тем допущением, что зенитный угол положения источника φi = 0. Анализ происходит в частотной области, поэтому временная зависимость, выражаемая экспонентой eiωt, исключается из рассмотрения. Так же проводимость сферы принимается нулевой, что несколько упрощает расчет (1), в противном случае аргумент сферической функции Бесселя становится комплексным (для полей внутри сферы).
При решении задачи с помощью тензорных функций Грина в расчетные выражения для рассеянного поля также будут входить сферические функции [3]. Помимо перечисленных выше, в коэффициентах разложения возникают функции Риккати – Бесселя. Некоторым упрощением данного подхода является достаточность нахождения функции Лежандра только первой степени. В работе [4] описан этот подход, который применяется для решения дифракционной задачи на неподвижной сфере с покрытием.
Сферические функции Бесселя
Основная сложность при вычислениях сферических функций Бесселя заключается в быстром нарастании ошибки вычисления, при приближении аргумента к особым точкам функции. В этом случае использование асимптотических приближений обязательно. Важным фактором является установление точных границ аргумента, при которых вместо прямого нахождения значения функции используются асимптотические зависимости. Эти границы устанавливаются с тем решающим фактором, чтобы точность асимптотических зависимостей начала превышать точность непосредственного нахождения. Из [1] получаем определение сферических функций Бесселя первого и второго рода:
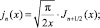
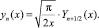(3)
Судя по выраженим, представленным там же, функции Бесселя первого и второго рода полуцелого порядка (n – целое число) имеют разложения в ряд и могут быть вычислены аналитически:
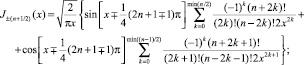
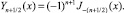(4)
Операция min(.) – округление дробного числа в меньшую сторону. Функции Риккати – Бесселя даются соотношением
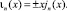(5)
Знак функции соответствует первому и второму роду функции.
Исходя из (1) n > 0, так же важно определить, в каких пределах может изменяться аргумент в рамках решаемой проблемы. Аргументом этой функции в (1) является произведение волнового числа и радиальной координаты системы отсчета. Очевидно, если приближаться к центру сферы, то R → 0, а значит, и весь аргумент будет стремиться к нулю. В противоположном случае, при расчете, поля в дальней зоне, а также для нахождения ЭПР сферы, R → ∞. Асимптотического поведения функции при увеличении аргумента нет, и представление (4) дает точный результат. Однако при очень больших аргументах максимальный порядок функции оказывается так же ограниченным для точного анализа. Так для x ~ 104, максимальный достоверно рассчитываемый порядок n = 54, что является более чем достаточным пределом суммирования в (1). Фактически результаты требуемой точности достигаются гораздо раньше.
При малых аргументах неточности аналитического расчета по выражению (4) могут быть значительными. Как известно, функции Бесселя обладают асимптотическими поведениями при x → 0. Для сферической функции Бесселя второго рода асимптотические приближения не используются, однако при очень малых значениях аргумента порядок может быть так же ограничен. Так при x ~ 10–4, n ≤ 50. Для определения границ начала использования асимптотического приближения сферической функции Бесселя первого рода полуаналитическому симулятору необходимо задать значения требуемой степени точности расчета Cl, что также является показателем последней значащей цифры после запятой. Единственным критерием при выборе этого значения является неравенство: Ωa/c > Cl, при Ω ≠ 0. В противном случае поля первого порядка будут меньше по амплитуде, чем вносимая в расчеты погрешность. После этого границы применимости приближений находятся решением уравнения (6) при заданном аргументе, относительно порядка функции:
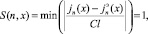(6)
где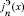 
– эталонная функция Бесселя, полученная вне рамок реализуемого симулятора. Уравнение (6) решается отдельно и для определенного набора значений Cl. При обнаружении симулятором наступления границ срабатывания S(n, x) функция Бесселя вычисляется по ее асимптотическому приближению:
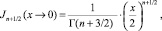(7)
где Г(.) – гамма-функция Эйлера.
На рис. 1 представлены полученные значения функции S(n, x) для двух значений Cl. Горизонтальной чертой показан единичный уровень, при котором для заданного аргумента симулятор начинает использовать выражение (7), начиная с соответствующего порядка. Как видно из рисунков, при нулевом пороге, равном 10–12, выражение (7) начинает использоваться симулятором для всех x < 10–1, уже для функций Бесселя первого порядка, в то время как при Cl = 10–6 для функций Бесселя первого порядка выражение (7) начинает применяться с x = 10–4. Исходя из этого факта можно сделать ряд выводов: первый – в окрестностях центра сферы расчет полей содержит ощутимую погрешность, и второй – задача не может быть решена для низких частот (k → 0). Первая проблема становится еще более ощутимой, если рассеиватель обладает проводимостью. Подобная задача рассматривается в [7]. В случае если сфера принимается идеально проводящей, а значит, электромагнитные поля внутри нее отсутствуют, подобная проблема перестает быть актуальной. Вторая проблема разрешается тем, что при низких частотах сфера малого радиуса может являться геометрической точкой, на которой отсутствуют дифракционные процессы. В общем случае такие ограничения являются обычными для подобной задачи.
Присоединенные функции Лежандра
В рамках этого исследования ставилась цель создать алгоритм аналитического расчета этих функций для требуемых значений, без использования численных методов. Необходимость такого алгоритма связана с тем, что существующие математические библиотеки дают определенное расхождение в результатах, полученных аналитическим путем. Так реализованный алгоритм сравнивался с алгоритмами вычисления присоединенных функций Лежандра, используемыми в широко известных ПО.
По определению функции [1] имеем
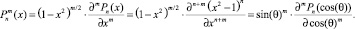(8)
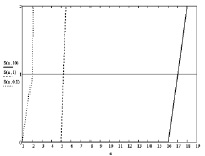
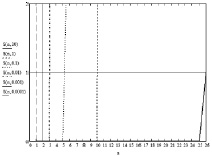
Рис. 1. Функция S(n, x) при Cl = 10–12 (слева) и при Cl = 10–6 (справа)
В некоторых случаях функция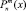 
имеет дополнительный множитель (–1)m, который называется фазой Кондона – Шортли. При решении данной задачи в его использовании нет необходимости.
Как видно из (8), аналитическое нахождение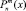 
подразумевает нахождение определенного количества производных от некоторой функции. При случайных наборах (R, θ, φ) точное разложение (1), главным условием которого является равенство модуля экспоненты единице, может достигаться при значениях n = 20 (или даже больше), что означает, в свою очередь, необходимость аналитического нахождения либо двадцатой производной от функции Лежандра, либо сороковой производной от степенной функции. Реализованный в симуляторе алгоритм основан на последовательном взятии производной, дифференцируя известное рекуррентное соотношение для первой производной [1] необходимое количество раз. При m = 0, 
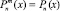, поэтому этот случай исключен из рассмотрения в алгоритме и задается явным образом.
Для обоснования алгоритма проводилось сравнение величин, полученных в сторонних ПО математических калькуляций, с аналитически полученными значениями. В силу того, что результаты двух вычислительных программ несколько различались, можно сделать вывод, что в них используются различные численные алгоритмы. Сравнения производились для произвольного угла θ при n = 20, а m изменялась от 0 до 10. В таблице приведены значения разностей соответствующих функций, полученных различными методами. Индекс «MC» – значения, полученные первой сторонней средой, «ML» – второй и «SIM» – в симуляторе, используя аналитический алгоритм.
Сравнение значений присоединенных функций Лежандра, полученных различными алгоритмами
|
m |
|
|
|
0 |
–5,995204333e–15 |
–1,9984014443e–15 |
|
1 |
2,2515322939e–13 |
9,9920072216e–14 |
|
2 |
5,6701310314e–12 |
1,9753088054e–12 |
|
3 |
3,1832314562e–12 |
3,592504072e–11 |
|
4 |
–6,0645106714e–8 |
–6,1845639721e–8 |
|
5 |
–2,0605511963e–8 |
3,061722964e–8 |
|
6 |
–4,8749148846e–5 |
–2,2136606276e–5 |
|
7 |
–2,3023039103e–4 |
–6,2820613384e–3 |
|
8 |
–9,965249896e–2 |
0,6451834142 |
|
9 |
–6,440164566 |
–65,2563529015 |
|
10 |
1,0952138901 |
2,7824062142e3 |
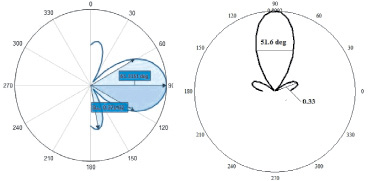
Рис. 2. Диаграммы рассеяния неподвижной сферы (a = 2 м, f = 100 МГц, εr = 16, μr = 1, θi = π/2). Слева диаграмма, полученная в САПР, справа - с помощью полуаналитического симулятора
Максимальная относительная ошибка для значений, указанных в таблице, в сравнении с первым ПО и предложенным алгоритмом, достигается для m = 10 и равняется 1,3·10–4 %. Очевидно – эта величина не является критической, однако при дальнейшем увеличении порядка дифференцирования в (8) она будет резко возрастать. Фактически при достижении предела суммирования в представленном случае относительная ошибка может стать значительной.
Выводы
Результаты работы симулятора сравнивались с данными, полученными с помощью известного САПР, использующего метод моментов. Важным допущением в этом случае является то, что анализировалась неподвижная сфера. Это обусловлено тем, что имеющийся программный продукт (как, впрочем, и его аналоги) не реализует функцию расчета рассеянного поля от вращающихся объектов. Более того, не существует адекватной возможности реконструировать среду распространения ЭМВ средствами этого ПО, чтобы она соответствовала среде распространения вращающейся сферы.
На рис. 2 показаны диаграммы рассеяния неподвижной диэлектрической сферы, приведены численные параметры этих зависимостей, по которым можно оценить их сходства и различия (ширина главного лепестка по уровню половины мощности и уровень боковых лепестков).
Результат, представленный на рис. 3, был получен при n = 3 в (1) и Cl = 10–10, что по времени расчета примерно совпадает с анализом сферы с числом разбиения на конечные элементы ~ 900.
В качестве главного вывода проделанной работы может выступать реализация симулятора, применяющего численные методы для расчета параметров вторичного поля, рассеянного от вращающихся тел, не имеющих строгого решения.