Дисперсионный анализ широко используется для обработки экспериментальных данных, поскольку он позволяет оценить влияние качественных признаков на количественные переменные [2, 4]. Причем многофакторный дисперсионный анализ, оценивая влияние взаимодействия факторов, содержит более конструктивные начала для научного исследования, чем однофакторный. Однако его применение вызывает трудности при содержательной интерпретации полученных результатов, которая должна раскрывать суть взаимодействия факторов высших порядков [3]. Как правило, ограничиваются рассмотрением интерпретации взаимодействий первого порядка (двух факторов). Однако в процессе изучения реальных явлений и процессов часто возникает необходимость учета взаимодействия трех и более факторов. Задача исследования влияния взаимодействия нескольких факторов на результативный признак является типичной в процессе изучения социально-экономических явлений [5]. Например, в маркетинговых исследованиях изучается влияние факторов «пол», «возраст», «время года» на спрос различных товаров, а также предпочтения их потребителей. Не обсуждая вопрос организации соответствующего исследования (в частности, факторного эксперимента), для анализа результатов которого и является подходящим многофакторный дисперсионный анализ, а также обоснованность выводов о причинных отношениях, в рамках данной статьи рассмотрим подход к интерпретации взаимодействия факторов второго порядка.
В данном случае проверяется гипотеза о влиянии взаимодействия второго порядка (трех факторов А, В, С) на один результативный признак (вариант ANOVA). Сформулируем нулевую гипотезу: влияние фактора А на результативный признак одинаково при разных градациях фактора В и С (аналогично для В и С). Тогда альтернативная гипотеза: влияние фактора А на результативный признак различно при разных градациях фактора В и С (аналогично для В и С).
Нулевая гипотеза предполагает, что средние в группах, отражающих взаимодействие второго порядка, равны. Необходимо разобраться, какие группы нужно сравнивать при анализе таких взаимодействий, учитывая, что они имеют место, если два фактора проявляют себя по-разному для разных градаций третьего фактора. Поясним это на простейшем примере, когда три фактора имеют по две градации. Полный экспериментальный план представим в виде графа-дерева. Обозначим градации фактора А «1» и «2»; фактора В «3» и «4»; фактора С «5» и «6». Градации фактора соответствуют вершинам графа, экспериментальную группу определяет соответствующий путь, например 135 (рис. 1–3).
Значит, для градаций фактора А (1 и 2) пары групп, соответствующие градациям фактора В (3 и 4), необходимо сравнивать по результативному признаку, т.е. сранивать нужно взаимодействия факторов В и С для разных градаций фактора А. Тогда взаимодействие трех факторов имеет место, если группы 35 и 36, 45 и 46 в одном случае (рис. 1, а) отличаются, а в другом случае (рис. 1, б) не отличаются или различия в средних другие.
Наглядно взаимодействия второго порядка представлены на графике взаимодействий. Однако по графику можно высказать только предположение о его наличии. Окончательный вывод делают на основании критерия Фишера, с помощью которого проверяется указанная выше нулевая гипотеза. Поскольку аналогичные комбинации можно получить для других факторов, то всего необходимо провести подобный анализ для трех пар групп (т.е. провести анализ трех графиков). Хотя графиков можно построить больше, выбирая из них более наглядный. В случае трех факторов нужно рассматривать три графика, которые дают различные интерпретации взаимодействия факторов.
В данном случае сравниваются следующие пары групп: 315 и 325 с 316 и 326; 415 и 425 с 416 и 426.
В данном случае сравниваются пары групп: 513 и 523 с 514 и 524; 613 и 623 с 614 и 624.
Если хотя бы в одном случае из трех на рис. 1–3 выявлены указанные различия, то взаимодействие второго порядка имеет место.
Рассмотрим пример, в котором все факторы межгрупповые фиксированные и полный экспериментальный план.
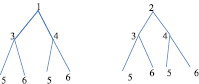
а б
Рис. 1. Структурные схемы полного экспериментального плана (вариант 1)
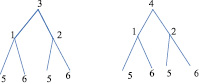
а б
Рис. 2. Структурные схемы полного экспериментального плана (вариант 2)
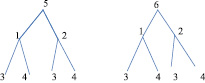
а б
Рис. 3. Структурные схемы полного экспериментального плана (вариант 3)
Пример. На компьютерном автотренажере изучались навыки вождения у двух групп испытуемых – новичков и опытных водителей (фактор А: 2 уровня: 1 – новички; 2 – опытные); испытуемые должны были проехать трассу трех типов сложности (фактор С: 3 уровня: 6 – низкая сложность, 7 – средняя сложность, 8 – большая сложность) в двух различных условиях вождения автомобиля – днем и ночью (фактор В: 2 уровня: 3 – день; 4 – ночь). Результативный признак – количество ошибок, допущенных водителями при каждом условии.
Результаты дисперсионного анализа (по критерию Фишера), выполненного в программе «Статистика», свидетельствуют о том, что есть факторные эффекты второго и первого порядков и все главные эффекты (заметим, что дисперсии по критерию Ливиня однородны). Анализ результатов начинают с интерпретации взаимодействия второго порядка. Приведем три разных графика взаимодействий для каждого из факторов.
Структура графиков может быть представлена в виде следующих графов (рис. 5).
Для всех графиков (градаций фактора С) факторы А и В проявляют себя одинаково (учитывая результаты апостериорного сравнения средних по LSD тесту):
– средние не отличаются в группах 315 и 325; 316 и 326; 317 и 327;
– средние отличаются в группах 415 и 425; 416 и 426; 417 и 427.
Это означает, что хотя и кажется, что на графике Var 4: 7 есть отличие во взаимодействии от других графиков, но по результатам сравнения данных групп этот вывод сделать нельзя. Рассмотрим второй график, который предполагает другой вариант сравнения групп.
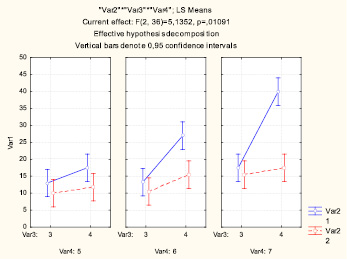
Рис. 4. Графики взаимодействия двух факторов для разных градаций фактора С
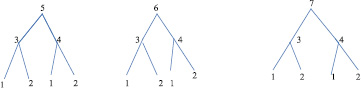
а б в
Рис. 5. Структурные схемы взаимодействия трех факторов, представленного на рис. 4
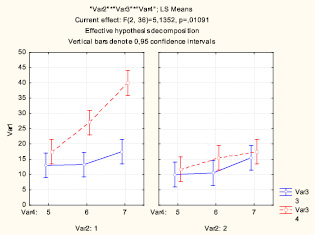
Рис. 6. Графики взаимодействия двух факторов для разных градаций фактора B
Структуру графиков представим в виде следующих графов (рис. 7).
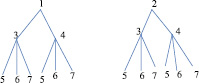
а б
Рис. 7. Структурная схема взаимодействия трех факторов, представленного на рис. 6
Сравним средние в группах на данных графиках.
1. На графике (а) средние в группах 137 и 147 отличаются, на графике (б) средние в группах 237 и 247 не отличаются.
2. На графике (а) средние в группах 136 и 146 отличаются, на графике (б) средние в группах 236 и 246 не отличаются.
3. На графике (а) средние в группах 135 и 145 не отличаются, на графике (б) средние в группах 235 и 245 не отличаются.
Утверждения в пунктах (1) и (2) свидетельствуют о том, что факторы В и С проявляют себя по-разному для разных градаций фактора А.
Содержательная формулировка заключается в следующем: ошибок больше ночью на трассе с повышенной сложностью (средней (6) и большой (7)) у новичков, в то время как время суток (день или ночь) и сложность трассы не имеет значения у опытных, т.е. днем новички делают одинаковое количество ошибок по сравнению с опытными только на трассе низкой сложности.
Третий вариант графиков изображен на рис. 8, а.
Или его альтернативный вариант (рис. 8, б).
Рис. 8,б удобнее для анализа, поскольку нужно сравнивать по две группы для каждой градации 5, 6, 7 фактора С.
1. Слева на графике средние в группах 351 и 352 не отличаются; справа на графике средние в группах 451 и 452 отличаются
2. Слева на графике средние в группах 361 и 362 не отличаются; справа на графике средние в группах 461 и 462 отличаются
3. Слева на графике средние в группах 371 и 372 не отличаются; справа на графике средние в группах 471 и 472 отличаются.
Утверждения в пунктах (1), (2) и (3) свидетельствуют о том, что факторы А и С проявляются себя по-разному для разных градаций фактора В.
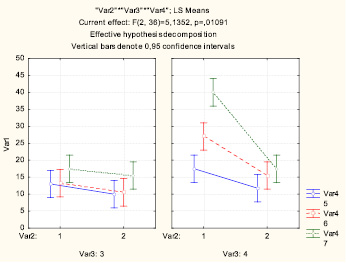
а
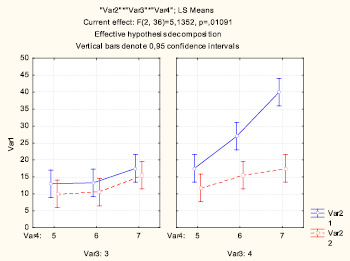
б
Рис. 8. а ? графики взаимодействия двух факторов для разных градаций фактора А; б ? графики взаимодействия двух факторов для разных градаций фактора А
Содержательная формулировка заключается в следующем: днем независимо от сложности трассы новички и опытные делают одинаковое количество ошибок, а ночью новички делают ошибок больше, чем опытные при низкой (5), средней (6) и большой (7) сложности трассы, т.е. новички делают ошибок больше ночью при любой сложности трассы.
Заметим, что на каждом из трех вариантов графиков смысл взаимодействия второго порядка, если оно установлено, должен быть разный. Кроме того, при апостериорном сравнении средних с помощью других тестов, например Шеффе и Бонфферони, могут быть получены другие результаты. По графику лишь приближенно судят о различии в средних и выдвигают только гипотезы. Окончательный вывод можно сделать, только используя результаты теста, желательно не одного, учитывая чувствительность каждого критерия к ошибке первого рода [1].
Очевидно, что при интерпретации результатов дисперсионного анализа при невыполнении всех его допущений могут возникнуть различные противоречия. Например, обнаруживаются различия между группами, которых при отсутствии взаимодействий второго порядка не должно быть. Это можно объяснить, в частности, нарушением однородности дисперсий. Хотя в случае отсутствия взаимодействия факторов интерпретацию обычно не выполняют (апостериорное сравнение средних).
В более сложном варианте многофакторного дисперсионного анализа, в частности, при смешанном экспериментальном плане возникает необходимость учета последовательности действия факторов, что, естественно, дополнительно усложняет интерпретацию взаимодействий второго порядка. В приведенном примере интерпретация взаимодействия факторов заключается в сравнении средних в разных группах. Вывод о влиянии этого взаимодействия на результативный признак можно сделать, лишь учитывая способы получения исходных данных (экспериментальные или неэкспериментальные) и условия организации факторного эксперимента в случае экспериментальных данных.



