Для решения поставленной задачи обратимся к рис. 1, где представлена схема трещины, заполненной проппантной набивкой, и направления движения потоков жидкости как в пласте, так и по трещине. Допустим, что фильтрационный поток жидкости в пласте является перпендикулярно направленным к трещине ГРП. Баланс потоков жидкостей в любой точке может быть представлен в соответствии с правилом токов в узле. В каждой выделенной точке трещины скорость фильтрационного потока определяется перепадом давления на этом элементе (согласно закону Дарси).
На плече ячейки имеем
J...J – 1 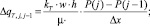 (1)
(1)
J + 1...J 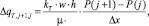 (2)
(2)
где ΔqT,j,j–1 и ΔqT,j + 1,j – изменение расхода потока жидкости в левой и правой частях ячейки; kТ – проницаемость трещины; w – раскрытость трещины; h – мощность пласта; μ – вязкость пластовой жидкости, расход в трещину, поступающий с стороны пласта P(J – 1), P(J), P(J + 1) – давления в узлах ячейки j – 1, j, j + 1, ∆x – шаг ячейки трещины.
Из пласта в выделенную ячейку трещины поступает поток жидкости с расходом
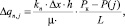 (3)
(3)
где Δqn,j – расход потока жидкости, поступающей из пласта в выделенную ячейку трещины ∆x; L – расстояние до контура питания, равное длине трещины; Рк – давление на контуре питания.
Баланс расходов в выделенной ячейке определится как
ΔqT,j,j–1 = ΔqT,j,j–1 + Δqn,j. (4)
Подстановка значений расходов в уравнение (4) приводит к
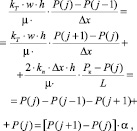 (5)
(5)
где 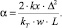
После представления последнего уравнения с выделением давления в узле j как неизвестного параметра, имеем
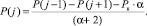 (6)
(6)
Расчет давлений в узлах сетки удобнее производить по методу Зайделя. Граничные условия на скважине, то есть на левой границе трещины (х = 0): Р = Рс, а на контуре питания, как уже указывалось, давление равно пластовому:
Р = Рпл = Рк. (7)
Проведем расчеты распределения давления в трещине для следующих значений параметров данной системы: проницаемость пласта равна 10 мД, ширина трещины (w) равна 0,01 м, толщина пласта (h) равна 10 м, шаг ячейки трещины (∆x) равен 1 м, длина трещины (LT) равна 150 м, давление на контуре питания (Рк) равно 100 атм., давление в скважине (Рс) = 50 атм.
Построим кривые распределения давления в пласте для различных значений проницаемости трещины, в диапазоне от 1 до 100 Д: kТ = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100 Д.
На рис. 2 представлены расчётные линии распределения давления по трещине для случая равномерного сопротивления движения потока жидкости в ней, а именно рассмотрен процесс фильтрации в трещине с конечной проводимостью и постоянной гидропроводностью.
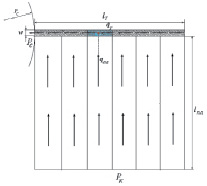
Рис. 1. Схема фильтрации жидкости в пласте и трещине
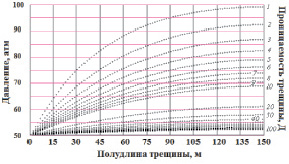
Рис. 2. Распределение давления в трещине для различных значении ее проницаемости
На рис. 2 видно, что для трещин с проницаемостями менее 10 Д имеется существенный перепад давления от конечного их участка до скважины. Для трещин с проницаемостью 1 Д давление на конце трещины практически равно пластовому давлению. Для трещин ГРП с проницаемостью 6 Д, перепад давления в трещине возрастает до величины, равной половины депрессии на пласт. Эти расчеты показывают, что перепады давления в трещине необходимо учитывать при оценке продуктивности скважин, подверженных массированному ГРП. Также при анализе данных графиков видно, что фильтрационный поток в пласте к трещине, для случая невысокой проводимости последней, не является линейным. Распределение полей давления в пласте при наличии конечной проводимости трещины представлено на рис. 3. Как видно, поток жидкости в зоне пласта, пересеченной трещиной, не является линейным.
На рис. 4 и 5 приведены расчетные графики, а в таблице представлены данные по увеличению продуктивности скважины ηгрп/η (где ηдо – продуктивность скважины до ГРП, ηгрп – продуктивность после ГРП) в зависимости от протяженности (Lт) и проницаемости трещины. Данные расчеты произведены также при условии, что скин-фактор до интенсификации был равен нулю, т.е. отсутствовало загрязнение призабойной зоны скважины.
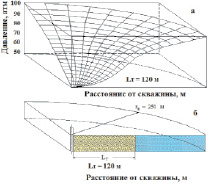
Рис. 3. Распределение давления в пласте при наличии сопротивления в трещине
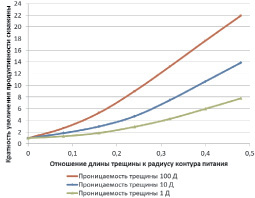
Рис. 4. Графики увеличения продуктивности скважины в зависимости от параметра α = Lт/Rк и проницаемости трещины (Sдо = 0)
Увеличение продуктивности скважины в зависимости от параметра α и проницаемости трещины, (α = Lт/Rк)
|
Параметр |
α = 0 |
α = 0,08 |
α = 0,16 |
α = 0,24 |
α = 0,32 |
α = 0,40 |
α = 0,48 |
|
k = 100 Д |
1,00 |
2,71 |
5,31 |
9,01 |
13,25 |
17,65 |
21,94 |
|
k = 10 Д |
1,00 |
1,84 |
2,98 |
4,72 |
7,49 |
10,69 |
13,89 |
|
k = 1 Д |
1,00 |
1,31 |
1,87 |
2,92 |
4,28 |
6,01 |
7,81 |
Поскольку во время бурения фильтрат бурового раствора проникает в пласт и тем самым загрязняет призабойную зону скважин, значение скин-фактора в скважинах до ГРП всегда имеет плюсовые значения. Это необходимо учитывать при планировании и прогнозе увеличения продуктивности скважин после интенсификации. В этой связи также стоит задача по расчету увеличения продуктивности скважин с учетом скин-фактора до гидроразрыва пласта. Такие расчеты были сделаны и представлены на рис. 6–8.
На рис. 6 представлен график увеличения продуктивности скважины после ГРП при проницаемости трещины 1 Д и для значений скин-фактора 5, 10, 15, 20 и 25. На рис. 7 представлен график увеличения продуктивности скважины после ГРП при проницаемости трещины 10 Д и для таких же значений скин-фактора. На рис. 8 все аналогично, но для трещины проницаемостью 100 Д.
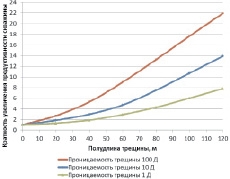
Рис. 5. Графики увеличения продуктивности скважины в зависимости от длины трещины и ее проницаемости, (Rk = 250 метров, Sдо = 0)
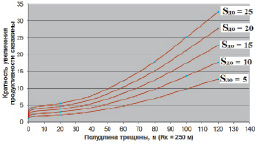
Рис. 6. График увеличения продуктивности скважины при проницаемости трещины 1 Д
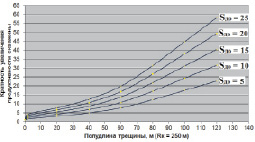
Рис. 7. График увеличения продуктивности скважины при проницаемости трещины 10 Д
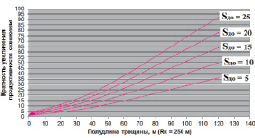
Рис. 8. График увеличения продуктивности скважины при проницаемости трещины 100 Д
Представленные графики (рис. 6–8) свидетельствуют, что на повышение продуктивности скважин после массированного ГРП существенно влияет степень загрязнения в ПЗП, то есть скин-фактор, который был до ГРП. Видно, что для трещины проницаемостью 1 Дарси и длиной более 100 метров, при нулевом скин-факторе до ГРП продуктивность скважины увеличится более чем в шесть раз. Для этих же условий, но со скин-фактором равным 25 до ГРП, продуктивность скважины в результате обработки уже повысится более чем в 25 раз. Поэтому для оценки кратности повышения продуктивности после массированного гидроразрыва пласта необходимо принимать во внимание значение скин-фактора до интенсификации.
Выводы
1. Разработана гидродинамическая модель фильтрации пластовой жидкости в системе «пласт ‒ трещина ‒ скважина», позволяющая наиболее достоверно решать стационарные задачи, связанные с технологией гидравлического разрыва пласта.
2. На основе численного моделирования решена задача и разработана методика по определению увеличения продуктивности скважин после МГРП, с трещиной конечной проводимости, а также при имевшем место загрязнении ПЗП до проведения интенсификации.
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ «Тюменский государственный нефтегазовый университет», г. Тюмень;
Сохошко С.К., д.т.н., заведующий кафедрой «Моделирование и управление процесcами нефтегазодобычи», Институт геологии и нефтегазодобычи, ФГБОУ «Тюменский государственный нефтегазовый университет», г. Тюмень.



