При эксплуатации строительно-дорожных машин, при самопроизвольном или преднамеренном изменении температуры в гидросистемах возникают сложные по конфигурации конвективные течения. Такого рода конвективные течения в зависимости от технологических условий могут быть необходимыми или нежелательными. В любом случае правильные технологические решения, связанные с возникающими конвективными течениями жидких или газообразных веществ, невозможны без их детального и всестороннего исследования, без понимания сути происходящих в них физических процессов. Именно с этим связана актуальность математического моделирования возникновения и последующего развития конвективных течений указанных веществ в замкнутых областях различной геометрической формы.
Ранее в работах [1, 2] была сделана попытка описать возникающее при нагреве подстилающей поверхности конвективное течение вязкого теплопроводного газа в замкнутой области в форме прямоугольного параллелепипеда. Причем нагрев осуществлялся в центре нижней грани расчетной области в виде круга конечного радиуса.
Целью же данной работы является численный расчет газодинамических характеристик в начальной стадии формирования трехмерного нестационарного конвективного течения газа как сжимаемой сплошной среды, вызванного локальным кольцеобразным прогревом нижней поверхности расчетной области.
При описании сложных течений жидкости и газа используется математическая модель упругой сплошной среды, основанная на решении полной системы уравнений Навье – Стокса [3–6]. Эта модель наиболее адекватно описывает физические процессы в указанных течениях, поскольку учитывает диссипативные свойства вязкости и теплопроводности.
Полная система уравнений Навье – Стокса записывается в безразмерных переменных с учетом действия силы тяжести и безразмерными значениями коэффициентов вязкости и теплопроводности μ0 = 0,001; κ0 ≈ 1,458333 μ0.
Эта система в дифференциальной форме передает законы сохранения массы, импульса и энергии в движущейся сплошной среде. А кроме того, через уравнения состояния корректно учитывает законы термодинамики.
Начальные условия при описании конвективных течений сжимаемой вязкой теплопроводной сплошной среды в случае постоянных значений коэффициентов вязкости и теплопроводности в данной работе берутся в виде набора пяти функций плотности, температуры и трех компонентов вектора скорости частиц, задающих известное точное аналитическое решение полной системы уравнений Навье – Стокса [7].
Расчетная область представляет собой куб с единичными безразмерными значениями сторон. Для плотности на всех шести гранях куба, исходя из неизменности потока за пределами расчетной области, ставится «условие симметрии» [8]. Это означает, что на граничной плоскости предполагается равенство нулю производной функции плотности в направлении нормали к граничной поверхности.
Для температуры на пяти гранях куба задаются условия теплоизоляции («условие симметрии») [8]. На нижней плоскости значения температуры в кольце между концентрическими окружностями с безразмерными значениями радиусов r = 0,1 и r = 0,3 заданы в виде функции, моделирующей кольцеобразный локальный нагрев нижней грани расчетного куба.
Краевые условия для компонент вектора скорости частиц сплошной среды на всех шести гранях соответствуют «условиям непротекания» для нормальной к граничной плоскости составляющей вектора скорости и «условиям симметрии» для двух других компонент вектора скорости течения [8]. Данные краевые условия фактически означают рассмотрение конвективного течения вязкой сжимаемой теплопроводной сплошной среды в непроницаемой и теплоизолированной кубической емкости.
Расчетная область заполняется трехмерной сеткой узлов пересечения трех семейств плоскостей с соответствующими разностными шагами по трем пространственным переменным.
Зная в начальный момент времени t = 0 во всех точках куба все искомые функции, с помощью явной разностной схемы вычисляют значения искомых функций в последующий момент времени во внутренних точках куба, во внутренних точках каждой из граней, ребер и вершин.
Расчеты проводились при следующих входных параметрах. Масштабные размерные значения плотности, скорости, расстояния и времени равны соответственно 1,2928 кг/м3, 333 м/с, 10 м, 0,03 с. Разностные шаги по трем пространственным переменным 0,01; 0,01; 0,1; а шаг по времени 0,001. Нагрев осуществлялся от температуры 15 градусов до 36 градусов по шкале Цельсия.
Проведенные расчеты показывают, что периферийные значения плотности, близкие к боковым граням расчетной области, для каждого отдельного фиксированного момента времени меняются незначительно. В центральной части боковых граней значения плотности больше, а в углах – меньше. Общее фоновое безразмерное значение плотности с течением времени увеличивается от 1 до 1,02, что соответствует изменению размерных значений в пределах от 1,2928 до 1,3187 кг/м3.
Распределение плотности в начале нагрева имеет форму кольца, центр которого совпадает с геометрическим центром квадратного сечения расчетной области, а радиус его совпадает с радиусом кольца нагрева. С течением времени происходит расширение кольца с повышенными значениями плотности и его размывание в пространстве вплоть до боковых граней расчетного куба.
С течением времени меняется и геометрическая симметрия плотности. В начале кольцеобразного прогрева нижней поверхности плотность газа имеет четко выраженную центральную симметрию, а с течением времени область центральной симметрии, расширяясь к боковым граням, меняется на прямоугольную.
Поведение рассчитанных значений температуры как функций координат и времени отлично от аналогичного поведения плотности. Периферийные значения температуры в начале прогрева также близки к единичному, а с течением времени наблюдаются немонотонные их изменения. В рассчитанном диапазоне временных шагов эти значения температуры меняются в пределах от 1 до 1,0025 (в размерных значениях от 15 до 15,72 °С).
Что касается геометрической симметрии, то с течением времени она для температуры практически не меняется со временем и сохраняет четко выраженную кольцеобразную центральную симметрию. Отличием поведения температуры от поведения плотности является существенно большее увеличение ее в центральной области до значений 1,01 (размерное значение 17,88 °С). Это увеличение температуры имеет вид колокола, что связано с более интенсивным прогревом центральной области. Кольцеобразный нагрев подстилающей поверхности, очевидно, сказывается на поведении температуры нагрева на фиксированной высоте в центральной части исследуемой области и визуализируется в виде воронки в центре колоколообразной поверхности.
Поведение первой компоненты скорости течения за рассчитанное время можно характеризовать следующим образом. В центре расчетной области скорости малы по значению, противоположны по знаку и имеют четко выраженную кольцевую структуру, соответствующую кольцевой схеме нагрева нижней плоскости. Положительные и отрицательные значения первой компоненты скорости, находящиеся за пределами кольцевого нагрева, описывают расходящееся от центра вдоль радиуса движение среды. Разные же по знаку скорости, но находящиеся внутри кольца нагрева соответствуют сходящемуся вдоль радиуса к центру потоку среды. Максимальные безразмерные значения модулей скоростей для данного расчетного момента времени составляют 2∙10–10 (размерное значение 6,66∙10–8 м/с).
Для 300 расчетного шага по времени (рис. 1) область, соответствующая движению среды от центра, расширяется, а область движения среды к центру сужается. При этом максимальные значения модулей скорости увеличиваются до 2∙10–5 (размерное значение 0,0067 м/с). Такие изменения первой компоненты скорости течения согласуются с нарастанием температуры кольцеобразного нагрева.
К 10000 расчетному шагу по времени область, соответствующая движению газа от центра, практически доходит до боковых граней. Максимальные значения модулей скорости увеличивается до 0,04 (размерное значение 13,32 м/с). Расчеты показали, что изменение x-ой компоненты скорости газа имеет ярко выраженный нестационарный характер. Кроме того, в начальные моменты времени общая структура скоростей имеет центральную симметрию, а с течением времени она изменяется и приобретает прямоугольный характер.
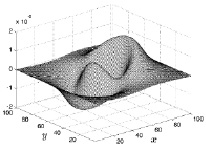
Рис. 1. Первая компонента скорости на 300 шаге по времени

Рис. 2. Вертикальная скорость на 300 шаге по времени
Характер поведения y-й компоненты скорости газа полностью аналогичен поведению x-й компоненты скорости газа, с той лишь разницей, что она описывает движение газа в направлении оси y. В результате, несмотря на принятую в расчетах прямоугольную систему координат, поведение первых двух компонент скоростей соответствует движению среды с центральной кольцевой симметрией. Поэтому нестационарный конвективный поток в условиях действия силы тяжести при такой схеме нагрева сохраняет центральную симметрию.
Вертикальная составляющая скорости течения в начальные моменты времени нагрева имеет кольцевой характер с очень малыми значениями 5∙10–8 (размерное значение 1,67∙10–5 м/с) и периферийными значениями, равными нулю. На 300 расчетном шаге по времени (рис. 2) периферийные значения вертикальной скорости по-прежнему близки к нулю, а кольцеобразная структура размывается в пространстве. При этом безразмерные значения вертикальной скорости 10–3 (размерное 0,333 м/с). С 2000 расчетного шага по времени периферийные значения вертикальной компоненты скорости становятся отрицательными и на 3000 расчетном шаге становятся равными –0,015 (размерное –5 м/с). В центре расчетной области значения вертикальной скорости также отрицательные, но имеют куполообразную форму со значениями, близкими к нулю. Такое пространственное распределение значений вертикальной составляющей скорости говорит о том, что движение газа с 2000 расчетного шага по времени направлено вертикально вниз и скорость этого движения больше на периферийных участках и меньше в центральной части расчетной области.
На рис. 3–4 представлены результаты расчета линий тока, выпущенных с плоскости z = 0, движущейся сплошной среды для двух расчетных шагов по времени.
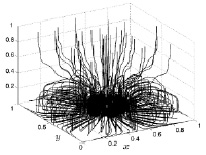
Рис. 3. Линии тока на 1500 шаге
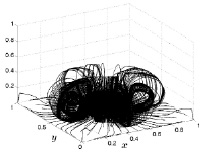
Рис. 4. Линии тока на 3500 шаге
Анализ построенных численно линий тока позволяет сделать следующие замечания относительно возникающего конвективного потока. К 500 расчетному шагу по времени линии тока в основном сосредоточены над источником кольцеобразного нагрева в виде тора, имеют значительную густоту и занимают часть пространства по высоте до 0,2 (размерное значение до 2 м). С точки зрения движения сплошной среды такое распределение линий тока к данному моменту расчетного времени означает формирование тороидального конвективного потока газа большой интенсивности вблизи источника нагрева подстилающей поверхности. Тот факт, что конвективный поток в основном расположен вблизи подстилающей поверхности, говорит о том, что прогрев основной части изолированного резервуара еще незначительный и конвективный поток не может преодолеть влияние силы тяжести.
По мере увеличения времени прогрева конвективный поток, захватывая все большие слои, увеличивается в размерах. Температура в кольце нагрева возрастает до значений, достаточных для преодоления силы тяжести вертикальным конвективным потоком (рис. 3).
Начиная с некоторого момента времени (конкретно с 3000 расчетного шага), начинается процесс уменьшения геометрических размеров потока (рис. 4). Из расчетов следует, что при сохранении большой интенсивности (густота линий тока) линейные размеры конвективного потока постепенно уменьшаются с течением времени и к 4000 шагу достигают высоты 0,2 (размерное значение 2 м) и радиуса 0,2 (размерное 2 м). Такое поведение конвективного течения объясняется, по-видимому, тем, что повышение температуры приводит к повышению давления в расчетном объеме и, как следствие, к сокращению размеров области конвекции.
Таким образом, для описания нестационарных трехмерных конвективных течений вязкой сжимаемой теплопроводной среды в замкнутой кубической области в данной работе рассматривается численное решение полной системы уравнений Навье – Стокса. Коэффициенты вязкости и теплопроводности полагаются постоянными. За начальные условия принимаются функции, являющиеся точным аналитическим решением полной системы уравнений Навье – Стокса. В качестве краевых условий предлагаются условия непротекания и теплоизоляции.
Возникающий при кольцеобразном нагреве нижней грани расчетной области конвективный поток газа в условиях действия силы тяжести имеет ярко выраженный нестационарный характер, отчетливо проявляющийся в начальной стадии его формирования.
Это касается как термодинамических характеристик потока – температуры, плотности и давления, так и скоростных характеристик. Результаты расчетов показывают, что все параметры имеют сложную структуру и существенным образом зависят от формы нагрева, высоты и времени нагрева. Кроме того, построенные линии тока частиц движущейся среды позволяют визуально представить сложный характер течения в исследуемой области.
Рецензенты:
Торопов С.Ю., д.т.н., профессор кафедры «Транспорт углеводородных ресурсов», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Захаров Н.С., д.т.н., профессор, заведующий кафедрой «Сервис автомобилей и технологических машин», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень.



