Задача о стационарных процессах в цилиндрических телах в случае, когда граница фазового перехода движется вдоль образующей, не меняясь, с постоянной скоростью, называется квазистационарной задачей Стефана. Такие задачи имеют большое прикладное значение, например, в металлургии, сварке и кристаллизации.
Математическая модель
Пусть пластина, имеющая ширину h и бесконечную длину, движется вдоль неподвижного теплового источника, задаваемого функцией g(x), отличной от нуля на отрезке [– α, α]. Направление движения совпадает с осью x. На достаточно большом расстоянии от теплового источника температура принимается равной нулю. Процесс будет описываться следующей квазистационарной задачей Стефана (рис. 1).
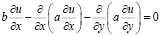
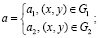
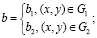
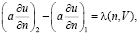
где n – нормаль к S = S1∪S2,V – вектор скорости;
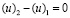 ;
;
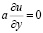 на
на 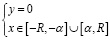
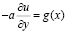 на
на 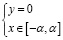 ;
;
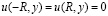 ;
;
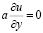 на
на 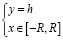 .
.
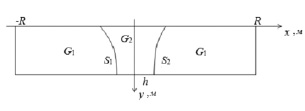
Рис. 1. G1 – твердая фаза, G2 – жидкая фаза
Рассмотрим следующую задачу: управляя тепловым потоком g(x), добиться минимального отклонения границы фазового перехода от заданной границы S.
Учитывая, что на границе фазового перехода S значение u равно температуре плавления θ, зафиксируем желаемую границу S и рассмотрим задачу минимизации функционала
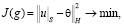
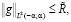 (1)
(1)
где 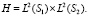
Представим функцию u(x,y) в виде суммы
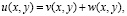
где v(x,y) – решение задачи
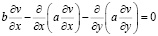 ;
;
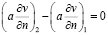 ;
;
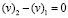 ;
;
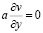 на
на 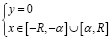 ; (2)
; (2)
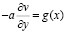 на
на 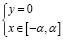 ;
;
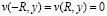
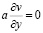 на
на 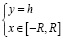 .
.
Если задача (2) при g(x) = 0 имеет только нулевое решение, то она однозначно разрешима в пространстве 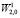 [5] для любой функции g(x)∈L2(– α,α) и будет выполняться неравенство [5]
[5] для любой функции g(x)∈L2(– α,α) и будет выполняться неравенство [5]
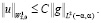 (3)
(3)
Рассмотрим оператор 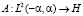 , сопоставляющий функции g след решения v задачи (2) на S.
, сопоставляющий функции g след решения v задачи (2) на S.
Теорема. Оператор А является непрерывным. Сопряженный оператор А* определяется равенством
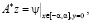
где ψ – решение следующей сопряженной задачи:
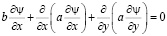 ,
,

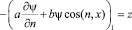 ,
,
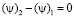 ,
,
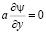 на
на 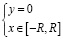 ,
,
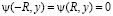 ,
,
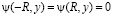 на
на 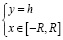 .
.
Доказательство. Непрерывность оператора A вытекает из неравенства (3) и теорем вложения. Формула для сопряженного оператора получается применением метода интегрирования по частям к равенству
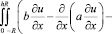
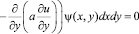 .
.
Теорема доказана.
Положим 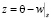 . Тогда задачу (1) можно переписать в виде
. Тогда задачу (1) можно переписать в виде
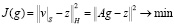 ,
,
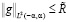 .
.
Пусть {ek} – базис в H, hi = А*ei. Критерий оптимальности будет иметь следующий вид [2]:
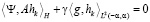
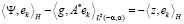
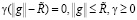 ,
,
где ψ = Ag – z
Пусть 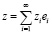 ,
, 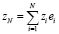 .
.
Рассмотрим аппроксимирующие задачи:
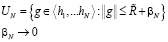
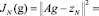
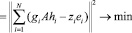 ,
,
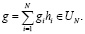
Для решения этих задач можно воспользоваться двойственным регуляризованным методом [4].
Для этого введем регуляризованные задачи
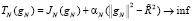 ,
,
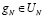 ,
, 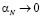 .
.
Введем функцию Лагранжа
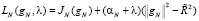 ,
,
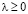 .
.
Решая двойственную задачу
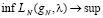
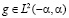 ,
,
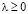 ,
,
найдем последовательность {gN} приближений оптимального управления g, которая будет в общем случае слабо сходиться к множеству оптимальных решений.
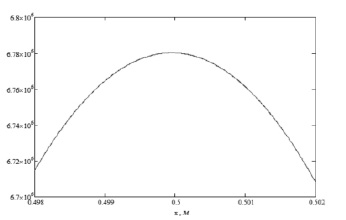
Рис. 2. График полученного источника gN
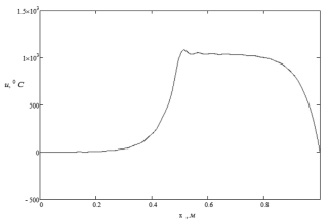
Рис. 3. График полученной температуры u (x, 0) на границе y = 0
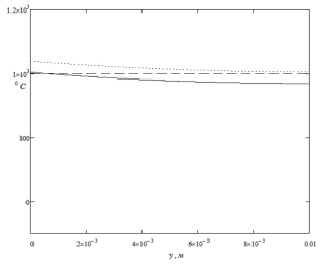
Рис. 4. Температура на S1 и S2: сплошной линией указана температура на S1, точечной линией указана температура на S2, пунктиром – заданная температура θ
Результаты вычислительных экспериментов
При решении задачи использовались следующие данные: S1 – отрезок x = – r, y∈[0, h], S2 – отрезок x = r, y∈[0, h], α = r = 0,002 м, R = 0,5 м, a1 = 155,7 Вт/(м×К) и a2 = 100Вт/(м×К) – теплопроводность в твердой и жидкой фазе соответственно, h = 0,01 м – толщина, θ 1000 °С – температура, b1 = c1ρ1V, b2 = c2ρ2V, где с1 = 1000 Дж/(кг×К) и с2 = 1000 Дж/(кг×К) – удельная теплоемкость в твердой и жидкой фазе соответственно, ρ1 = 2600 кг/(м3) и ρ2 = 2300 кг/(м3) – плотность в твердой и жидкой фазе соответственно, V = 0,001 м/с – скорость, λ = ρ1k, где k = 315000 Дж/кг – теплота плавления, N = 40.
В качестве базиса в пространстве Н использовалась следующая система векторов:
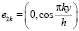 ,
, 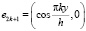 .
.
Решение сопряженной задачи находилось методом Галеркина как решение, удовлетворяющее соответствующему интегральному тождеству.
Рецензенты:
Чермных В.В., д.ф.-м.н., доцент, профессор кафедры фундаментальной и компьютерной математики, ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров;
Шатров А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования в экономике, ФГБОУ ВПО «Вятский государственный университет», г. Киров.
Работа поступила в редакцию 30.12.2014.



