Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Развитие экономики всецело зависит от степени обоснованности принимаемых управленческих решений и степени практической реализации этих решений. Принимаемых решений, даже применительно к отдельно взятому экономическому объекту, множество, и их обоснование требует наличия большого объема информации, которую надо систематически собирать, накапливать, обрабатывать, анализировать и хранить.

Как известно, чтобы управлять экономическим объектом, требуется последовательно выполнять три группы управленческих функций: связанных с учетом и отчетностью; аналитических и связанных с прогнозированием. Каждая группа функций имеет свое самостоятельное назначение. Чтобы обеспечить эффективное управление объектом, требуется выполнение этих групп функций в их взаимосвязи и взаимообусловленности. При этом следует отметить особую роль аналитических функций в цепочке трех групп функций, поскольку требуется анализировать данные учета и отчетности, собственно аналитические данные и прогнозные данные.

В одном исследовании невозможно рассмотреть все многообразие функций, их принципов, методов и особенностей. Поэтому в настоящем исследовании рассматриваются методы, модели, информационное обеспечение и методика разработки и обоснования прогнозов экономических показателей путем выявления тенденций их изменения, количественного выражения в виде моделей и экстраполяции этих тенденций на прогнозируемый период.

В качестве объекта исследования выбраны показатели сводной годовой отчетности о численности работников и заработной плате хозяйств системы Минсельхоза Республики Дагестан за 2005–2012 гг.

Существует множество трактовок понятия прогноз. В конечном итоге эта сущность сводится к следующей [см. например, 2; 7]: прогноз – это обоснованное суждение о возможном состоянии экономического объекта в будущих или альтернативных путях и сроках достижения этих состояний, которое основывается на расчетах неизвестных экономических показателей по заданным значениям факторов с помощью моделей.

Процесс разработки прогноза называют прогнозированием. Под ним понимают систему научных исследований качественного и количественного характера, направленных на выяснение тенденций развития народного хозяйства или его частей (отраслей, регионов, предприятий и т. п.) и поиск оптимальных путей достижения целей этого развития.

Принято различать качественные и количественные методы прогнозирования. Количественные методы применяются в том случае, если деятельность в прошлом имела определенную тенденцию, которую можно количественно выразить и продолжить в будущем, и когда имеющейся информации достаточно для выявления статистически достоверных тенденций или зависимостей.

При количественном методе прогнозирования применяются известные методы экстраполяции и интерполяции, сущность которых состоит в переносе знаний о прошлых событиях на события будущего, а также в нахождении промежуточных значений величины по имеющемуся набору известных значений [7].

В настоящее время в различных сферах экономики создаются специальные компьютерные системы для прогнозирования, позволяющие совместно применять различные методы и модели. Кроме того, крупные государственные и частные организации создают так называемые «ситуационные комнаты», в которых группа высококвалифицированных экспертов анализирует ситуацию, имея доступ к различным банкам статистических данных и базам знаний, пользуясь различными видами математических и имитационных моделей.

Иными словами, принятие обоснованных управленческих решений, связанных с развитием экономики и её различных звеньев, требует разработки и внедрения в практику экономического управления информационных систем и технологий.

В настоящее время информатизация в различных отраслях экономики и сферах управления находится на разных уровнях. Если в финансово-банковской сфере, в сфере налоговых органов и в ряде других сфер управления экономикой информатизация находится на достаточно высоком уровне, то на предприятиях (организациях, учреждениях) отраслей экономики она находится на недопустимо низком уровне.

В отраслях промышленности уровень информатизации относительно выше, в сельском хозяйстве он практически находится на нулевом уровне, особенно в регионах.

Для позитивного изменения ситуации с информатизацией в сельском хозяйстве требуется принять срочные меры. Особенно это относится к таким регионам, как Республика Дагестан, который считается депрессивным регионом. Следует отметить, что преобладание в экономике удельного веса сельского хозяйства (более одной трети ВРП) является одной из причин депрессивности экономики.

Разработка информационной системы АПК Республики Дагестан для всех уровней управления (хозяйства (предприятия), административные районы, регион в лице Министерства сельского хозяйства республики) путем создания её различных компонентов (подсистем и комплексов, модулей и автоматизированных рабочих мест) является одной из актуальных и важных задач, к решению которой следует приступить безотлагательно. Отметим, что работы по разработке подобных информационных систем для сферы АПК не ведутся и в других регионах страны.

Одним из компонентов такой системы должна стать подсистема информационного обеспечения подготовки принятия решений для лиц, ответственных за эти решения и их практическую реализацию.

В течение ряда лет нами ведутся исследования по разработке различных модулей для системы подготовки принятия решений в сфере АПК РД. Один из модулей предназначен для анализа и выявления динамических тенденций развития сельского хозяйства РД, их количественного выражения в виде различных моделей, а также для разработки вариантов прогнозов, предусматривающих разные траектории дальнейшего развития сельского хозяйства. В модуле реализованы решения, базирующиеся на методах статистики и эконометрического моделирования. Часть модуля, предназначенная для прогнозирования, предусматривает экстраполяцию тенденций изменения: показателей к предыдущему или базисному году; удельных весов тех или иных составляющих в суммарных величинах показателей; экономических показателей с помощью различных видов уравнений временных рядов и рядов динамики.

Прогнозируемые значения каждого показателя в отдельности в модуле предусматривается рассчитать тремя способами:

– путем экстраполяции динамики изменения показателя (темпов роста или прироста);

– с помощью встроенных статистических функций «тенденция» и «рост» из MS Excel, представляющих собой уравнения временных рядов линейного и показательного видов;

– с применением заранее построенных уравнений временных рядов.

Первый способ представляет собой вариант реализации на ПЭВМ метода классической статистики.

Второй способ позволяет автоматизировать прогнозные расчеты с помощью функций «тенденция» и «рост», являющиеся уравнениями временных рядов линейного и показательного видов. При этом способе строить сами уравнения временных рядов не требуется. Недостатком этого способа является выполнение прогнозных расчетов без предварительного проведения сравнительной оценки степени приемлемости двух применяемых уравнений временных рядов, как между собой, так и с другими из возможных их видов.

Сущность 3-го способа состоит в том, что в этом случае в процессе построения уравнений временных рядов рассчитываются их статистические характеристики и с их помощью проводится сравнительный анализ приемлемости каждого из уравнений для выполнения на их основе прогнозных расчетов.

Одним из элементов новизны настоящего исследования является разработанная нами методика применения функций «тенденция» и «рост». Функцию «тенденция» можно использовать и для выполнения прогнозных расчетов с помощью уравнений временных рядов гиперболического (Yt = b + m/t), параболического (Yt = b + m1∙t + m2∙t2) и степенного (Yt = b∙tm) видов, а функцию «рост» – для прогнозирования с помощью уравнения показательного вида (Yt = b∙mt).

Методика прогнозирования с применением уравнений временных рядов включает следующие шаги:

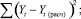
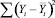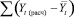– рассчитываются статистические характеристики для уравнений временных рядов линейного, гиперболического и параболического видов с помощью встроенной функции «ЛИНЕЙН», величины Yрасч; и (где Yt, Yt(расч),  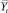– фактические, расчетные и среднее арифметическое значения зависимого показателя Yt), а также стандартная ошибка для Yt (sey), t-критерий Стьюдента и средняя ошибка аппроксимации 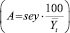для всех пяти видов уравнений;

– с помощью пяти уравнений временных рядов рассчитываются варианты прогнозов на 2013–2015 гг., подставляя в построенные уравнения временных рядов значения для t, равные 9, 10 и 11 (соответствующие для 2013, 2014, 2015 гг.), и определяются доверительные интервалы для прогнозных значений;

– проводится сравнительный анализ различных вариантов прогнозов, а также формулируются выводы о степени их приемлемости и реальности.

Ниже приведены уравнения временных рядов:

а) для среднегодовой численности работников категории «Все работники»:

Xt = 28540,0 – 2532,5t; R = 0,9238; (1)

Xt = 29796,6∙0,8778t; R = 0,9566;

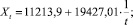
R = 0,8717; (2)

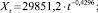R = 0,9574;

Xt = 35793,0 – 7367,9t + 604,4t2;

R = 0,9959; (3)

б) для средней годовой зарплаты на одного работника категории «Все работники»:

Yt = 8644,6 + 6967,5t; R = 0,9363; (4)

Yt = 13362,1∙1,2536t; R = 0,6471;

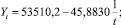R = 0,9372; (5)

Yt = 13235,5∙t0,7500; R = 0,9468;

Yt = –1656,7 + 13835,1 – 858,4t2; R = 0,9403.

Уравнения временных рядов наиболее простые из видов моделей, применяемых для прогнозирования. Их преимуществом по сравнению с методами классической статистики является возможность прогнозирования каждого показателя с помощью различных видов уравнений. Недостаток состоит в том, что каждый из показателей прогнозируется в отдельности без учета влияния на них различных факторов и без учета их взаимовлияния друг на друга.

Поэтому более обоснованным является прогнозирование с помощью уравнений рядов динамики. Речь при этом идет об обоснованности прогноза для зависимого показателя. Таким показателем в нашем случае является средняя годовая заработная плата на одного работника, которая зависит от численности работников. Ниже приведены пять видов уравнений рядов динамики, выражающие зависимость средней годовой заработной платы на 1 чел. от численности работников по категории «Все работники», и величины индекса детерминации (R), характеризующие степень тесноты корреляционной связи:

Линейный Yt = –1656,7 + 13835,1 – 858,4t2; R = 0,9502.

Показательный 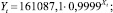R = 0,9897.

Гиперболический 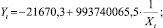R = 0,9937.

Степенной 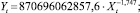R = 0,9934.

Параболический 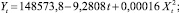R = 0,9970.

Методика расчета прогнозных значений для зависимого показателя уравнений рядов динамики состоит в следующем:

– строятся уравнения рядов динамики пяти видов, выражающие зависимость средней годовой заработной платы на 1 чел. от численности работников по методике аналогичной для уравнений временных рядов, а также уравнения временных рядов для среднегодовой численности работников;

– по уравнениям временных рядов рассчитываются прогнозные значения численности работников;

– рассчитываются прогнозные величины для средней годовой заработной платы на 1 чел. (Yt – зависимого показателя), подставляя в уравнения рядов динамики Yt = f(Xt) прогнозные величины для численности работников (Xt – независимого показателя);

– проводится сравнительная оценка вариантов прогнозных значений зависимого показателя, рассчитанных с помощью различных видов уравнений рядов динамики между собой, а также с вариантами прогнозов, рассчитанными с помощью уравнений временных рядов.

В таблице приведены величины средней годовой заработной платы на 1 чел. на прогнозные периоды, рассчитанные с помощью трех видов уравнений рядов динамики, выражающих зависимость средней годовой заработной платы от численности работников.

Прогнозные величины средней годовой заработной платы на 1 чел., рассчитанные с помощью трех видов уравнений рядов динамики, выражающих зависимость средней годовой заработной платы от численности и уравнений временных рядов для численности работников (по категории «все работники»)

Как видно из таблицы, по показателю «средняя годовая заработная плата на одного работника» для одной категории работников (в нашем случае для категории «все работники») с помощью пяти видов уравнений рядов динамики требуется рассчитать по пять вариантов прогнозов.

При этом в качестве исходных данных для показателя «среднегодовая численность работников» используются прогнозируемые значения, рассчитанные по пяти уравнениям временных рядов. В итоге для каждой категории работников рассчитывается 15 вариантов прогнозов.

Задача лиц, ответственных за обоснованный выбор прогнозных решений, состоит в сравнительном анализе этих вариантов и выборе одного, двух или трех из них для последующей реализации.

На основе рассчитанных вариантов прогнозов можно составлять и «гибридные» варианты прогнозов: как средние арифметические или средние взвешенные двух, трех и т.д. вариантов.

Встроенные функции MS Excel вполне приемлемы для расчета параметров всех пяти рассматриваемых видов уравнений временных рядов и рядов динамики. Однако эти функции не позволяют проводить сравнительные оценки степени приемлемости исследуемых видов уравнений для практического применения, в частности при прогнозировании.

Дополнительные статистические характеристики, рассчитываемые с помощью функции «ЛИНЕЙН» для уравнений линейного, гиперболического и параболического видов, являются сопоставимыми для сравнительной оценки приемлемости этих видов уравнений. Однако ряд дополнительных статистических характеристик для уравнения степенного вида рассчитываются функцией «ЛИНЕЙН» не по исходным данным Yt и t, а по их логарифмам. Поэтому статистические характеристики для степенной функции в этом случае не сопоставимы с характеристиками других видов уравнений. Аналогичное дело обстоит и с функцией «ЛГРФПРИБЛ», используемой для расчета параметров и статистических характеристик уравнения показательного вида.

Кроме того, функциями «ЛИНЕЙН» и «ЛГРФПРИБЛ» не предусмотрен расчет таких важных статистических характеристик, как t-критерий Стьюдента и средняя ошибка аппроксимации (А) и ряд других.

Поэтому целесообразно все дополнительные статистические характеристики рассчитывать по единой методике. Такая методика для расчета наиболее значимых данных статистических характеристик разработана нами. Методика предполагает создание совокупности взаимосвязанных таблиц, а также алгоритмов расчетов, включающей встроенные статистические функции из MS Excel и ряд важных формул из эконометрики, отсутствующие в среде MS Excel.

Основу методики составляют шесть групп таблиц, среди которых особого внимания заслуживают: таблицы фактических (Yt) и расчетных (Yt(расч)) значений численности и заработной платы по каждому виду уравнения для каждой категории работников; таблицы, предназначенные для расчетов

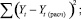
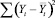
и

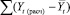
(где Yt, Yt(расч), 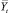 – фактические, расчетные и среднее арифметическое значения зависимого показателя Yt); таблицы, представляющие собой сводные таблицы всех дополнительных статистических характеристик.

С нашей точки зрения, прогноз показателей численности работников в сфере АПК и их заработной платы следует проводить как методами классической статистики, так и методами эконометрического моделирования. Такой подход и заложен в разработанный нами компьютерный модуль.

Алиев М.А., д.э.н., профессор кафедры экономической теории, ФГБОУ ВПО «Дагестанский государственный педагогический университет», г. Махачкала;

Кутаев Ш.К., д.э.н., зав. отделом воспроизводства населения и трудовых ресурсов, Институт социально-экономических исследований, Дагестанский научный центр РАН, г. Махачкала.