Процедуры встраивания цифрового водяного знака (далее ЦВЗ) имеют ряд приложений, включающих защиту цифровой информации, судебные доказательства при помощи меток и ЦВЗ, задачи перевода цветного изображения в полутоновое и другие. Большинство из этих приложений сейчас интенсивно разрабатываются в силу следующих причин. Информация часто представлена в цифровой форме и имеются эффективные инструменты для обработки цифровых сигналов и изображений. В самом деле, цифровые изображения – это наиболее распространенный тип медиа, для которых в настоящее время доступны стеганографические приложения.
Среди основных проблем встраивания ЦВЗ особенно выделяется проблема устойчивости к преобразованиям стегоизображения, которые могут приводить к разрушению встроенных данных. Так как для изображений стандартом де-факто стал формат JPEG, который вносит искажения в оригинал в связи с сжатием с потерями, поэтому разработка методов создания и встраивания ЦВЗ, устойчивых к JPEG-сжатию, является актуальной задачей.
ЦВЗ могут быть получены разными способами, в нашем случае ЦВЗ представляет собой цифровое бинаризированное изображение, полученное путем бинаризации полутонового. Разные алгоритмы бинаризации генерируют ЦВЗ, они встраиваются с секретным ключом в плоскости Грея. Потом осуществляется запись в JPEG, это сжатие с заданным параметром качества. Извлекая ЦВЗ после сжатия и анализируя меры искажения, можно найти, какие алгоритмы бинаризации генерируют более устойчивые ЦВЗ, обеспечивая тем самым секретность и устойчивость стегосистемы.
Цифровое растрирование является процессом уменьшения битовой глубины изображения для воспроизведения на устройствах, способных к репродуцированию меньшего числа уровней серого, чем тех, которые представлены в оригинальном изображении с высокой битовой глубиной (так называемое изображение с непрерывным тоном). Напечатанные изображения, которые, казалось бы, имеют непрерывные тона, созданы оригинальным распределением точек при использовании растрового алгоритма. К алгоритмам бинаризации предъявляют различные требования. Хороший растровый алгоритм должен так преобразовывать информацию, чтобы обеспечить вывод с высоким визуальным качеством. Помимо этого он должен быть помехоустойчивым и быть простым с вычислительной точки зрения.
В настоящей статье развивается стеганографическая система для встраивания бинаризированных ЦВЗ в плоскости Грея полутонового изображения. Добавлен секретный ключ для повышения секретности и используются современные алгоритмы бинаризации.
Коды Грея хорошо известны в теории информации [7]. Построенные с их помощью плоскости Грея для случая цифрового изображения позволяют выделить одно из его главных свойств – избыточность, что представляет интерес для современной стеганографии, которая занимается встраиванием цифровых данных.
Плоскости Грея получаются из битовых плоскостей и определяют представление изображения в пространственной области. Для пространственной области описано большое число методов встраивания цифровых данных, или ЦВЗ [11], среди которых варианты LSB (Least Significant Bit), блочное и аддитивное встраивание, где используется битовое представление.
После того как бинаризированные данные встроены, полученное стегоизображение сохраняется в формате JPEG, который осуществляет сжатие с потерей, которое может разрушать ЦВЗ. Однако JPEG очень широко используется на практике, поэтому в литературе уделяется большое внимание стеганографии, устойчивой к JPEG-сжатию (см., например, [5, 6]). Встраивание ЦВЗ в jpg-файл с последующим JPEG-сжатием известно как J2J (JPEG-to-JPEG) преобразование [17]. Оно изучалось во многих работах, где представлены методы, предлагающие разнообразные компромиссы между уровнем сжатия и деградацией ЦВЗ.
Цель нашей работы – рассмотреть встраивание бинаризированного изображения, полученного алгоритмом бинаризации, в плоскости Грея с секретным ключом с последующим JPEG-сжатием. Методы встраивания в плоскости Грея, предложенные в [16] и развитые в [9, 10, 18], продемонстрировали их устойчивость к RS (Regular-Singular) анализу, атакам типа χ2 и SPA (Sample Pair Analysis). Детекторы для обнаружения ЦВЗ, которые построенны на основе SPA, могут иметь высокую эффективность [13], однако их проектирование сильно усложняется при использовании битовых плоскостей, начиная со второй [14]. В нашей работе для встраивания выбрана шестая плоскость Грея, детектор для которой авторам не известен. В отличие от приведенных работ, где рассматривались разнообразные атаки, мы интересовались устойчивостью к JPEG-сжатию при использовании секретного ключа.
Получение бинаризированного ЦВЗ при помощи алгоритма бинаризации
Вместо бинарного (не бинаризированного никаким алгоритмом бинаризации) или полутонового представления ЦВЗ предлагается использовать бинаризированное изображение, как вход в стегосистему с плоскостями Грея и секретным ключом. Процесс бинаризации можно рассматривать как преобразование яркости, когда элемент f(x, y), где x = 1, 2, .., M, y = 1, 2, ..., N, M×N – размер изображения, матрицы полутонового изображения, принимающий 2k значений, где k = 1, 2, ..., в общем случае преобразуется в матрицу R, состоящую из нулей и единиц:
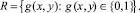
Для получения бинаризированного ЦВЗ воспользуемся следующими алгоритмами бинаризации. Д-алгоритм – алгоритм бинаризации на основе равенства яркостей [8]. Д-алгоритму было посвящено большое число работ авторов и был проведен его анализ устойчивости к шумам [12], в котором найдено что алгоритм является помехоустойчивым и является простым с вычислительной точки зрения. Также были использованы алгоритмы, представленные на коде Си с интегрированными mex-функциями из [15]. Они были вызваны в MATLAB с применением компилятора языка программирования Си. Из алгоритмов, относящихся к классу частотно-модулированного растрирования, были выбраны следующие: Bayer, использующий пороговый массив, стандартный алгоритм Флойда – Стейнберга Errdif, основанный на дитеринге с использованием голубого шума, модификация алгоритма Флойда – Стейнберга Dotdif, модификация Ulichney с возмущенными весами, модификация Lau с адаптивным гистерезисом. Также для сравнения был выбран алгоритм Cdod, выполняющий дитеринг с формированием печатных точек в виде кластеров, принадлежащий классу алгоритмов амплитудно-модулированного растрирования. При этом размер, частота растра, форма точки и угол растра могут отличаться.
Представление полутонового изображения с помощью плоскостей Грея
Коды Грея для пиксела с получаются из двоичного представления его яркости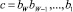 
с помощью соотношения gW = bW и gV = bV + bV+1, V < W, где все gV, bV Î 0,1. Здесь и далее все биты складываются по модулю два. Двоичные разряды bV имеют вес 2V–1, V = 1, ..., W, где старший разряд W. Для кодов Грея это не так, поскольку они относятся к системам счисления с неестественными весами. В полутоновом изображении совокупность одноименных двоичных разрядов bV образует битовую плоскость. Это бинарное изображение BV, где пиксел имеет два значения яркости. Аналогично совокупность кодов Грея gV будем называть плоскостью Грея GV, которая также является бинарным изображением. Любое полутоновое изображение можно представить с помощью плоскостей Грея.
Пусть C – это 8-битовое полутоновое изображение. Его представление через битовые плоскости имеет вид
.
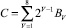Из определения кода Грея следует, что
B8 = G8,
BT = G8 + ... + GV + GT, (1)
где T < 8. Отсюда вытекает важное свойство, которое используется дальше. Так, согласно (1) модификация одной плоскости Грея, например, GV приводит к модификации сразу нескольких битовых плоскостей B1, ..., BT, ..., BV. В итоге представление 8-битового изображения имеет вид [2, 3]
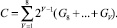(2)
Алгоритмы встраивания и детектирования с секретным ключом
Будем рассматривать задачу встраивания ЦВЗ – бинаризированного изображения M в полутоновое, используя заданную плоскость Грея, с секретным ключом. Для этого возьмем простой алгоритм побитового сложения
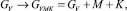
который представляет собой вариант метода LSB в пространственной области. Ключ K является случайной бинарной матрицей, равной размеру ЦВЗ. В результате получается стегоизображение с секретным ключом:
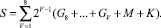(3)
Согласно выводам, полученным в наших работах [1, 3], мы используем встраивание бинаризированного ЦВЗ в плоскости Грея и извлечение из плоскости Грея при не слепом детектировании, так как этот вариант показал хорошие результаты для мер искажений [1], при этом необходимо исходное изображение. Для этого случая сокрытое бинаризированное изображение M можно извлечь из плоскости Грея GVMK стегоконтейнера S, путем побитового сложения
M = GVMK + K + GV.
Сжатие с потерей
Формат JPEG осуществляет сжатие с потерями, это сложный процесс, который будем описывать преобразованием
A → Aq,
где q = 1, 2, ..., 100 – параметр качества. Он представляет собой вес, с которым используются матрицы квантования DCT (Discrete Cosine Transform) коэффициентов в формате JPEG. Большие значения q соответствуют высокому качеству и, соответственно, низкой степени сжатия.
Рассмотрим следующую схему, которая включает сжатие. Бинаризированное изображение M встраивается в плоскость Грея GV полутонового контейнера C с ключом K. В результате получается стегоизображение S, которое сжимается вместе с контейнером.
M, K, C → S;
C, SG → CqSGq.
Затем осуществляется вариант не слепого D′ детектирования. Для него потребуется плоскость Грея GVq сжатого контейнера Cq, плоскость Грея GVMKq сжатого стегоконтейнера Sq и исходный несжатый ключ K.
Эксперимент
Цель эксперимента – выяснить, какие алгоритмы бинаризации, с помощью которых получен ЦВЗ, обеспечивают меньшее искажение при JPEG-сжатии. Для этого были вычислены меры искажения d(M, X) между бинаризированным изображением M и извлеченным после сжатия X = Mg. В качестве мер были выбраны евклидово расстояние e(M, X), пиковое отношение сигнал/шум PSNR(M, X) и относительная энтропия Q(M, X), характеризующая различие гистограмм [4].
На рис. 1 показана работа этого алгоритма. В полутоновое изображение C (рис. 1, a) встраивается бинаризированное изображение M, с ключом K, представляющим собой шум. Для встраивания выбрана шестая плоскость Грея для наглядности, чтобы специально показать, что будет просвечивать не ЦВЗ, а только шум.
а б в
г
Рис. 1. Встраивание бинаризированного изображения в полутоновое с секретным ключом: а – полутоновый контейнер; б – бинаризированный ЦВЗ; в – ключ; г – стегоконтейнер с бинаризированным ЦВЗ в V = 6 плоскости Грея
На рис. 2 представлены компоненты ЦВЗ Mga, где a = 1, 2, ..., 7, встроенные в плоскость Грея G6 полутонового контейнера (рис. 1, а) и извлеченные из плоскости Грея после сжатия с параметром качества q = 70, 80, 99 при не слепом детектировании.
ЦВЗ Mga, где a = 1, 2, ..., 7, получен при помощи набора современных алгоритмов бинаризации – DOTDIF – Mg1, ERRDIF – Mg2, LAU – Mg3, ULICHNEY – Mg4, CDOD – Mg5, BAYER – Mg6, основанных на диффузии ошибки, и оригинального Д-алгоритма Mg7.
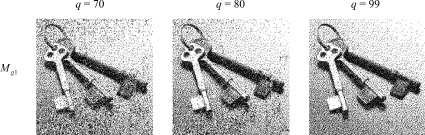
Рис. 2. ЦВЗ, извлеченные из плоскости Грея G = 6 для 7 алгоритмов бинаризации после сжатия с параметрами качества q = 70, 80, 99 (начало)
Рис. 2. ЦВЗ, извлеченные из плоскости Грея G = 6 для 7 алгоритмов бинаризации после сжатия с параметрами качества q = 70, 80, 99 (окончание)
Визуальное качество у Mg7 лучше. Эта особенность может быть связана с тем, что алгоритмы, использующие в своей основе стохастический процесс, уже содержат шумы в несжатых бинаризированных копиях. Добавление секретного ключа и операция сжатия с потерями негативно сказывается на визуальном качестве ЦВЗ, приводя к негативным эффектам типа усиления рассеивания, дальнейшего снижения контраста, потере границ, видимости шумов.
Однако изображение, бинаризированное Д-алгоритмом, которое извлечено из плоскости Грея после сжатия, имеет не только более высокое визуальное качество, но и хорошие меры искажения (рис. 3), полученные на интервале сжатия q = [85:99]. Убывающий характер e(M, X) (рис. 3, а) и увеличение PSNR(M, X) (рис. 3, в) при увеличении q свидетельствует о правильной работе алгоритмов бинаризации и выбранных мер искажения. Алгоритм Mg7 показывает приемлемые результаты для e(M, X) и PSNR(M, X), и имеет наименьшую среди рассмотренных алгоритмов относительную энтропию Q(M, X) при достаточно больших значениях степени сжатия (q ≥ 90) (рис. 3, д), что означает, что устойчивость к зашумлению и JPEG-сжатию у Д-алгоритма высокая.
Далее работоспособность предложенного алгоритма встраивания и детектирования была протестирована на 36 полутоновых изображениях из коллекции Caprichos, Francisko Jose de Goya. Эти изображения имеют очень сложную текстуру, что служит хорошим признаком при выборе контейнера для встраивания цифровых данных. Для параметра качества q ≥ 50 эта область представляет наибольший интерес. При встраивании в плоскость Грея с не слепым детектированием из плоскости Грея результаты рассчитанных мер искажения при q = [50:99] продемонстрировали монотонность убывания e(M, X) и возрастания PSNR(M, X) (рис. 5 а, в).
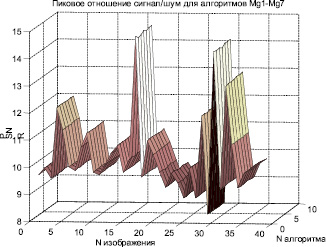
Усредненные по параметрам качества значения e(M, X), PSNR(M, X) для тестового набора из 36 изображений для всех алгоритмов бинаризации приведены на рис. 4.
Для всех изображений коллекции меры искажения Д-алгоритма сопоставимы с мерами искажения остальных рассмотренных алгоритмов (рис. 5, б, в).
Зависимости d(M, X) от q = 50, 60, 70, 80, 90, 99, усредненные по 36 картинкам, приведены на рис. 6.
Согласно рассчитанным мерам искажения, при q = 60 минимальное значение e(M, X) имеет алгоритм Mg4, Д-алгоритм Mg7 идет вторым (рис. 5, б). Для PSNR(M, X) при q = 60 (рис. 5, г) алгоритм Mg7 показывает максимум – что показывает хорошую устойчивость алгоритма бинаризации Mg7 к шумам, возникшим при введении ключа и сжатии. График относительной энтропии (рис. 5, д) свидетельствует о хорошей работе Д-алгоритма (черная линия) и означает меньшую разность гистограмм по сравнению с другими алгоритмами и, как следствие этого, большую помехоустойчивость и лучшее визуальное качество. Зависимость Q(M, X) свидетельствует согласно [18] о следующем:
а) предложенный алгоритм встраивания и детектирования имеет наивысший уровень секретности для алгоритма Mg7;
б) алгоритм бинаризации Mg7 является наиболее помехоустойчивым.
Рис. 3. Меры искажения при извлечении ЦВЗ после JPEG-сжатия: а – евклидово расстояние; б – евклидово расстояние при q = 91, 92; в – пиковое отношение сигнал/шу
м; г – пиковое отношение сигнал/шум при q = 96, 97; д – относительная энтропия; е – относительная энтропия при q = 93
а б
в
Рис. 4. Зависимости мер искажений для алгоритмов Mga: а – полутоновый контейнер; б – евклидово расстояние; в – пиковое отношение сигнал/шум
Из найденных зависимостей следует, что предложенный метод встраивания и детектирования может быть полезным для крипто-устойчивых задач стеганографии, требующих последующего сжатия, а для получения бинаризированного ЦВЗ предпочтительнее использовать Д-алгоритм бинаризации.
Выводы
В статье выполнено оригинальное научное исследование, посвященное компьютерной стеганографии. Плоскости Грея цифрового изображения наряду с битовыми плоскостями могут быть использованы для сокрытия бинаризированного изображения. Для алгоритмов типа LSB встраивание в плоскость Грея эквивалентно использованию нескольких битовых плоскостей. Особенности проявляются при JPEG-сжатии стегоизображения. Это преобразование возникает естественным образом, когда изображение с ЦВЗ сохраняется на диске в jpg-файле. В статье рассмотрен вариант не слепого детектирования. Найдено, что для детектирования из плоскости Грея предпочтительнее использовать сжатую плоскость Грея GVq сжатого контейнера Cq, нежели чистую плоскость Грея GV контейнера C. Найдено, что для лучшего детектирования с использованием сжатых плоскостей Грея ключ K сжимать не требуется.
Рис. 5. Зависимости мер искажений для алгоритмов Mga от q = 50, 60, 70, 80, 90, 99: а – евклидово расстояние; б – евклидово расстояние при q = 60; в – пиковое отношение сигнал/шум; г – пиковое отношение сигнал/шум при q = 60; д – относительная энтропия; е – относительная энтропия при q = 90
Проведен анализ набора алгоритмов бинаризации, найдено, что Д-алгоритм бинаризации цифровых изображений показывает хорошие результаты для введения в плоскости Грея с секретным ключом и обеспечивает устойчивость к сжатию типа JPEG. Авторы доказали, что оригинальный Д-алгоритм способен производить ЦВЗ, устойчивые к сжатию. Доказательство основано на найденных значениях мер искажения и субъективной визуальной оценке. Из расчетов, проведенных для массива изображений, следует, что предпочтительнее использовать Д-алгоритм для получения бинаризированного ЦВЗ, а для его внедрения в полутоновое изображение применять плоскости Грея и секретный ключ. Алгоритмы, написанные на базе пакета MATLAB, являются оригинальными и могут быть полезны как для практического использования в задачах защиты цифровых изображений, так и в учебном процессе для демонстрации базовых методов стеганографии.
Работа выполнялась по тематикам госбюджетных НИР № 11.9217.2014, № 11.9170.2014, проводимых в 2014 году, в рамках государственных заданий Министерства образования РФ.
Рецензенты:Казаков А.Я., д.ф.-м.н., профессор, ФГБОУ ВПО «Санкт-Петербургский государственный университет технологии и дизайна», Северо-Западный институт печати, г. Санкт-Петербург;
Бригаднов И.А., д.ф.-м.н., профессор, «Национальный минерально-сырьевой университет «Горный»», г. Санкт-Петербург.
Работа поступила в редакцию 27.12.2014.