Случайные процессы являются моделями многих реальных процессов и занимают значительное место в современных прикладных исследованиях. Теория случайных процессов находит широкое применение: в радио- и электротехнике, кибернетике; в математической экономике и математической биологии, в молекулярной теории газов и др. Раздел, посвященный теории случайных процессов, имеется в рамках курса «Теория вероятностей и математическая статистика», который входит в базовую часть профессионального цикла (Б.3) ООП бакалавриата по направлению подготовки 010400.62 «Прикладная математика и информатика» [4].
Целью освоения модуля «Теория случайных процессов» является фундаментальная подготовка бакалавров в области построения и анализа различных стохастических моделей, овладение современным математическим аппаратом для дальнейшего использования его в прикладных исследованиях.
Современный этап развития общества, характеризующийся всеобщей информатизацией, непрерывной сменой технологий, постоянным изменением структуры и содержания информационных ресурсов, в значительной мере повышает требования к информационной подготовке будущего бакалавра. При изучении теории случайных процессов решение многих задач значительно упрощается с использованием математических пакетов.
В работах [5–7] описаны возможности применения компьютера при обучении студентов теории вероятностей и математической статистике.
Среди множества программных продуктов можно выделить такие системы компьютерной математики, как MathCad, Matlab, Mathematica, Maple и др. Все они обладают широкими возможностями для решения задач различных классов, имеют большое число встроенных функций, средства символьных преобразований, анимации и визуализации.
Выбор нами среды MathCad для изучения теории вероятностей и математической статистики обусловлен ее специфическими возможностями [5–7]. Важнейшей такой возможностью является то, что система позволяет генерировать выборки распределенных с произвольными параметрами случайных величин. Благодаря этому, мы имеем возможности для модуляции различных случайных процессов. Кроме того, в Mathcad к сгенерированным случайным процессам достаточно легко применять статистические методы обработки данных (например, строить гистограммы, производить спектральный и корреляционный анализ).
На основе источников [1–3] нами разработан лабораторный практикум по теории вероятностей и математической статистике, предполагающий использование данного пакета в качестве среды для моделирования. В качестве примера использования MathCad при изучении теории случайных процессов выберем один из наиболее значимых разделов дисциплины – «Цепи Маркова» ‒ и решим следующую типовую задачу.
Пусть начальное распределение вероятностей состояний цепи Mapкова задано вектором а(0) = (0, 0, 0, 1), а матрица переходных вероятностей имеет вид
Вычислить: вероятности состояний цепи Маркова в течение 5 шагов; безусловные вероятности состояний цепи Маркова на 5-м шаге, а также номер интервала, в котором содержится число 1. Найти частоты различных состояний в m траекториях цепи, каждая из которых содержит n шагов.
Решение. Введем матрицу переходных вероятностей Р и вектор вероятностей состояний на нулевом шаге а:
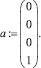
Затем введем функцию Pr(а, P, n), позволяющую вычислять вероятности состояний цепи Маркова в течение n шагов:
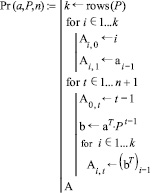
При n = 5 имеем
.
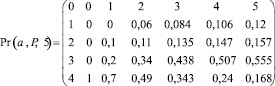В результате мы получили матрицу, строки которой соответствуют номерам состояний (они указаны в нулевой строке), а столбцы соответствуют номерам шагов, которые указаны в нулевом столбце.
К примеру, вероятности состояний на втором шаге равны: для первого 0,06, второго 0,11, для третьего 0,34 и четвертого – 0,49.
Безусловные вероятности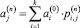 
, (n = 1,2,…) состояний цепи Маркова на n-м шаге найдем с помощью функции UnPr(a, P, n) (а – это вектор вероятностей состояний на нулевом шаге):
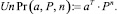
При n = 5
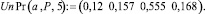
Теперь введем функцию Def(a, x), которая позволяет определять номер интервала i, содержащего число х:
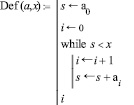
Для х = 1
Def(a, 1) = 3.
С помощью функции Ch(a, P, n, m) вычислим частоты различных состояний в m траекториях цепи, причем каждая из них содержит n шагов.
Детерминированное моделирование цепи Маркова в течение n шагов осуществляет функция ModCh(a, P, n, RN), выдавая одну траекторию для заданного вектора RN.
В качестве входных переменных при этом используются:
1) вектор а, который определяет начальное распределение вероятностей состояний цепи;
2) матрица Р вероятностей переходов между состояниями за шаг;
3) вектор RN, содержащий (n + 1) компонент RNi (RNi < 0 < 1), использующихся для определения состояний цепи Маркова на различных шагах.
Заметим при этом, что RN0 применяется для выработки начального состояния цепи в соответствии с распределением а, остальные же компоненты – для выработки состояний на шагах 1, 2,…, n. Данная функция используется в модуле, который реализует основную функцию ImModCh(a, P, n, m), генерирующую значение вектора RN (m – число моделируемых траекторий). Этот модуль позволяет осуществлять имитационное моделирование цепи Маркова в течение n шагов. Функция ImModCh() в качестве результата возвращает матрицу, строки которой соответствуют номеру шага, а столбцы – номеру реализации. На пересечении строки и столбца – номер состояния на данном конкретном шаге в соответствующей реализации.
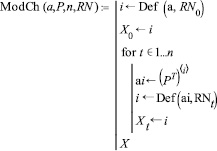
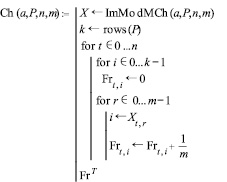
Присвоив значения: n = 5, m = 10000, получим
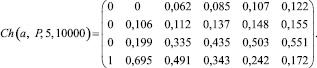
Как видим, применение математического пакета позволило нам избежать рутинных вычислений, значительно сократить время, затраченное на решение задачи, и при этом получить результат с достаточно высокой степенью точности.
К достоинствам решения исследовательских учебных задач в компьютерной среде следует отнести предоставленные пользователю возможности варьировать параметры в задаче в достаточно широких пределах и при необходимости манипулировать математическими моделями случайных процессов. При этом необходимо отметить, что использование компьютера не заменяет традиционные средства обучения, а дополняет их, являясь элементом системы средств обучения, ориентированной на использование информационных технологий.
Известно, что успешная профессиональная подготовка будущих бакалавров предполагает реализацию системы общепрофессиональных и профессиональных компетенций обучающихся. Изучение теории случайных процессов с использованием информационных технологий обеспечивает инструментарий формирования следующих общекультурных и профессиональных компетенций подготовки бакалавра «Прикладная математика и информатика»:
– способность использовать в научной и познавательной деятельности, а также в социальной сфере профессиональные навыки работы с информационными и компьютерными технологиями (ОК-14);
– способность работы с информацией из различных источников, включая сетевые ресурсы сети Интернет, для решения профессиональных и социальных задач (ОК-15);
– способность демонстрации общенаучных базовых знаний естественных наук, математики и информатики, понимание основных фактов, концепций, принципов теорий, связанных с прикладной математикой и информатикой (ПК-1);
– способность приобретать новые научные и профессиональные знания, используя современные образовательные и информационные технологии (ПК-2);
– способность понимать и применять в исследовательской и прикладной деятельности современный математический аппарат (ПК-3);
– способность осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников (ПК-6);
– способность собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным, профессиональным, социальным и этическим проблемам (ПК-7).
Таким образом, внедрение информационных технологий в учебный процесс при изучении теории случайных процессов создает благоприятные условия для эффективного обучения студента в информационно-образовательной среде; у будущих бакалавров углубляются фундаментальные и прикладные знания, развиваются творческие способности, самостоятельность, вероятностное мышление, математическая и информационная культура.
Рецензенты:Попов В.Н., д.ф.-м.н., доцент, зав. кафедрой математики, ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», г. Архангельск;
Сотникова О.А., д.п.н., доцент, проректор Ухтинского государственного технического университета, г. Ухта.
Работа поступила в редакцию 16.12.2014.