В статье рассматривается дифференциальное уравнение вида
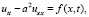
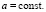 (1)
(1)
Оно описывает малые поперечные, продольные и крутильные колебания однородного стержня. Обычный способ решения такого уравнения состоит в отыскании решения в виде бесконечного тригонометрического ряда [1, 3, 5]. В данной работе предлагается метод, дающий решение в конечном виде.
1. Вначале найдём общее решение уравнения (1). Перейдём к новым переменным 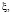
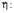
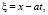
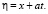 (2)
(2)
Функция 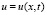 перейдёт в функцию
перейдёт в функцию 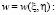
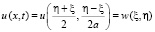 ,
,
и уравнение (1) приведётся к виду
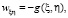 (3)
(3)
в котором
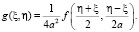 (4)
(4)
Интегрирование уравнения (3) по переменной 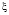 даст
даст
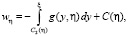 (5)
(5)
где 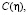
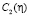 – произвольные функции. Проинтегрировав (5) по
– произвольные функции. Проинтегрировав (5) по 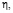 получим
получим
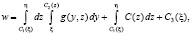 (6)
(6)
где 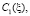
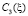 – произвольные функции.
– произвольные функции.
Пусть 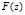 – первообразная функция от
– первообразная функция от 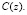 В этом случае
В этом случае
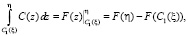
и (6) запишется в виде
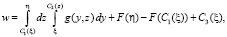
Введём обозначения
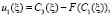
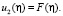
Тогда
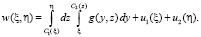 (7)
(7)
Заменив 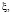
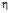 по формулам (2), получим общее решение исходного уравнения
по формулам (2), получим общее решение исходного уравнения
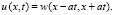
2. В качестве примера применения данного метода решим уравнение (1), в котором положим 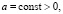 взяв область изменения переменных
взяв область изменения переменных
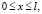
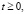 (8)
(8)
начальные условия
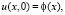
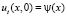 (9)
(9)
и однородные граничные условия
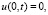
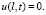 (10)
(10)
Выполнив в (1) замену
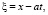
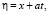 (11)
(11)
получим уравнение вида (3):
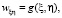 (12)
(12)
общее решение которого даётся равенством (7). Представим это равенство в виде
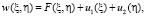 (13)
(13)
где
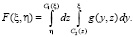 (14)
(14)
Из (11) следует
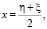
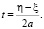
Из этих равенств вытекают соответствия:
 (15)
(15)
Поэтому из (8) получается следующая область 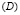 изменения переменных
изменения переменных 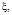
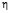 (рисунок):
(рисунок):
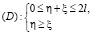
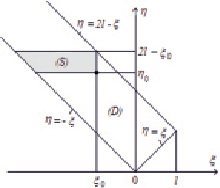
Неограниченная полоса (D) – область изменения переменных ξ, µ (S) – область, принятая в качестве области интегрирования в двойном интеграле
Внутри 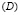 возьмём произвольную точку
возьмём произвольную точку 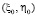 и построим участок
и построим участок 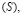 как показано на рисунке. Этот участок задаётся системой неравенств
как показано на рисунке. Этот участок задаётся системой неравенств
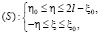 (16)
(16)
В соответствии с (14) значение функции 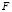 в точке
в точке 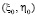 равно
равно
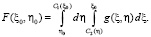
Область интегрирования определяется системой неравенств
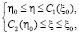 (17)
(17)
В силу произвольности функций 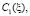
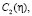 выберем их такими, чтобы система неравенств (17) совпала с (16):
выберем их такими, чтобы система неравенств (17) совпала с (16): 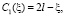
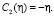 Выражение (14) примет вид
Выражение (14) примет вид
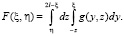 (18)
(18)
Из (18) следует
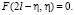 (19)
(19)
Привлечём условия (9) – (10), чтобы найти оставшиеся функции 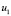 и
и 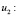
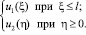 (20)
(20)
Запишем условия (9)–(10) в переменных 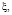
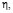 используя соответствия (15):
используя соответствия (15):
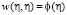 при
при 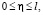 (21)
(21)
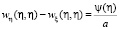 при
при 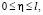 (22)
(22)
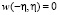 при
при 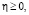 (23)
(23)
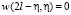 при
при 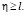 (24)
(24)
Подставим эти значения в (13):
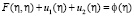 при
при 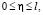 (25)
(25)
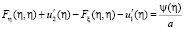 при
при 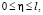 (26)
(26)
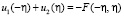 при
при 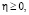 (27)
(27)
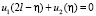 при
при 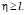 (28)
(28)
При получении (28) учтено равенство (19). Запишем первые два уравнения в виде
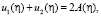 (29)
(29)
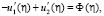 (30)
(30)
где обозначено
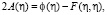
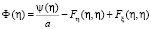 (31)
(31)
при 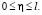 Проинтегрировав (30) в пределах от 0 до
Проинтегрировав (30) в пределах от 0 до 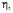 будем иметь
будем иметь
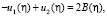 (32)
(32)
где
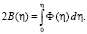 (33)
(33)
Из (29) и (32) находим
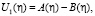 при
при 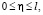 (34)
(34)
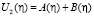 при
при 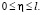 (35)
(35)
Получились формулы, определяющие
функции 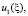
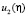 при
при 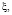
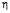

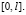 Они обозначены
Они обозначены 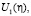
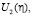 потому что, опираясь на них, далее будем искать формулы, определяющие
потому что, опираясь на них, далее будем искать формулы, определяющие 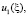
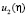 при остальных значениях
при остальных значениях 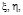 лежащих в
лежащих в 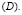
Из (27) имеем
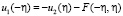 при
при 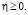 (36)
(36)
При 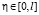 правая часть определяется по формуле (35), поэтому
правая часть определяется по формуле (35), поэтому
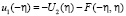 при
при 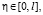
отсюда
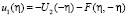 при
при 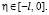
Таким образом,
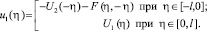 (37)
(37)
Мы нашли формулу, задающую 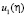 при
при 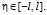 По этой формуле получим
По этой формуле получим
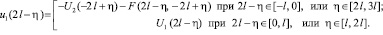 (38)
(38)
Из (28) имеем
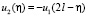 при
при 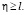 (39)
(39)
Подставим (38) в (39):
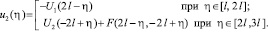 (40)
(40)
Подставим (40) в правую часть равенства (36) и заменим 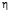 на
на 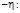
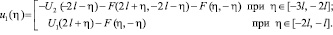 (41)
(41)
Эта формула определяет 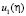 при
при 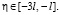 В (41) заменим
В (41) заменим 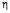 на
на 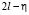 и потребуем, чтобы
и потребуем, чтобы 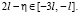 Будем иметь
Будем иметь
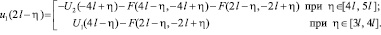
Подставим это выражение в (39):
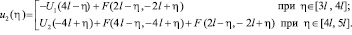
И так далее. Обнаруживаются следующие закономерности, определяющие 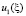 и
и 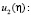
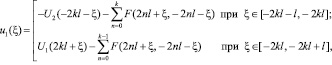 (42)
(42)
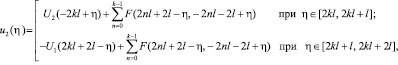 (43)
(43)
Формулы (42), (43) дают решение задачи. В них считается, что 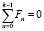 при
при 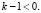 Непрерывность этих функций на концах интервалов обеспечивают соотношения
Непрерывность этих функций на концах интервалов обеспечивают соотношения
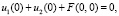
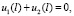
вытекающие из (27) и (28).
3. Итак, задачу
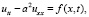
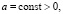
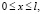
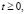
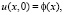
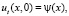
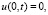
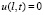
можно решить последовательным нахождением следующих величин:
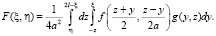
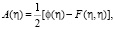
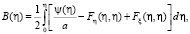
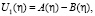 при
при 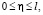
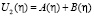 при
при 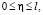
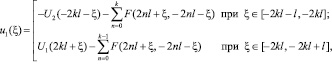
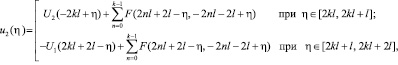
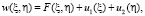
и находим, наконец,
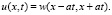 (44)
(44)
Рецензенты:
Габдрахимов М.С., д.т.н., профессор, заведующий кафедрой «Нефтепромысловые машины и оборудование» филиала ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Октябрьский;
Арсланов И.Г., д.т.н., профессор, заведующий кафедрой «Механики и технологии машиностроения» филиала ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Октябрьский;
Шамолин М.В., д.ф.-м.н., профессор ведущий научный сотрудник Института механики МГУ им. М.В. Ломоносова, г. Москва.
Работа поступила в редакцию 02.09.2014.



