Исследования по методу функциональных биомеханических проб (ФБМП) приводят к получению дискретных массивов отсчетов сигналов, соответствующих ответным реакциям биообъекта на стандартизованные (дозированные) механические воздействия [1, 2, 7]. В представленной ранее статье [4] рассматривалась компонентная обработка сигналов ФБМП на основе интерполяционных полиномов Лагранжа и Гаусса с целью выбора наилучшего из этих полиномов с точки зрения информативности коэффициентов разложения. Однако применение степенных полиномов для интерполирования приводит при большом числе отсчетов к необходимости вычислять определители, члены которых различаются на много порядков, что делает вычисления неустойчивыми. Применение тригонометрического полинома Гаусса при интерполяции функций с большим числом отсчетов требует включения в число базисных функций компонентов с высокими частотами, которые фактически не наблюдаются в реальном физическом процессе (являются артефактами). Это заставляет искать более удобные в вычислительном отношении, а также мало чувствительные к числу отсчетов методы анализа и соответствующие им множества базисных функций.
Как будет показано далее, на роль такого множества может претендовать система ортогональных функций Хаара [6]. Особенностью базиса Хаара является то, что каждая функция является причинно–обусловленной. Более того, каждая компонента одного порядка учитывает момент «включения» очередного причинно–обусловленного преобразования [3]. Кроме того, базис Хаара, как известно, является полным и ортогональным, что весьма существенно облегчает вычисления, а также фактически воспроизводит сигнал в виде ступенчатой функции независимо от числа отсчетов. Это представляется важным в свете построения общей методики компонентного анализа сигнала, содержащего данные реакций ФБМП.
Поскольку компонентный анализ данных ФБМП имеет конечной целью создание методик массового скринингового обследования, то очевидно, что способы обработки и содержательной интерпретации таких данных должны быть, согласно сложившейся практике, простыми, допускать удобное графическое представление. Все процедуры анализа признаков, объединения (интеграции) данных и их представления врачу–специалисту для принятия решений должны быть в максимальной степени автоматизированы. Ниже будет построена дискретная схема анализа на основе системы дискретных ортогональных функций Хаара.
Разложение вектора отсчетов наблюдаемого сигнала 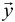 по дискретным базисным функциям Хаара связано с решением системы линейных алгебраических уравнений вида
по дискретным базисным функциям Хаара связано с решением системы линейных алгебраических уравнений вида
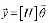 , (1)
, (1)
где H – квадратная матрица порядка nхn, составленная из столбцов, каждый из которых представляет собой набор последовательных значений базисных функций 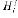 ,
, 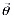 – вектор коэффициентов разложения. Решение системы (1) имеет вид
– вектор коэффициентов разложения. Решение системы (1) имеет вид
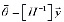 . (2)
. (2)
Обращение [H] можно упростить, используя свойство полноты и ортогональности базиса Хаара.
Домножая обе части (1) на [H–1], получим
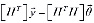 . (3)
. (3)
Учитывая ортогональность, заключаем, что [HTH] – диагональная матрица с одинаковыми диагональными элементами hii=n, i=1,…,n.
С учетом этого получаем
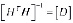 , где
, где 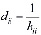 . (4)
. (4)
Тогда окончательно получаем
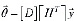 . (5)
. (5)
Легко оказать, что (5) эквивалентно (2). Действительно,
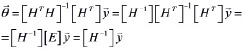 (6)
(6)
Очевидно, что (5) – это формула обращения матрицы H, которую легче реализовать программно, особенно при больших размерностях матриц (числах отсчетов измеряемого сигнала).
Рассмотрим пример. Матрицу H базисных функций Хаара легко задать, используя рекуррентное определение
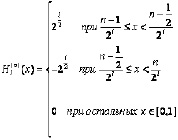 (7)
(7)
где 0 ≤ log2n, 1 ≤ n ≤ 2l; n – количество функций в базисе. Сразу отметим, что для полноты системы функций необходимо n брать равным 2, 4, 8, …, т.е. 2k.
При n=8 [6] приводит к следующему виду матрицы H (8):
 ,
,
 . (8)
. (8)
Матрица D, согласно (4), примет вид (9)
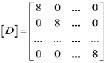 ,
,  . (9)
. (9)
Тогда
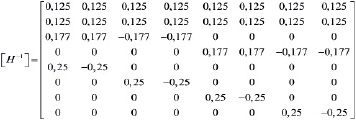 . (10)
. (10)
Рассмотрение выражений (7)–(10) с точки зрения вычислительной сложности показывает, что с ростом n (числа отсчетов) эта сложность растёт линейно. Другой аспект интерполирования сигналов в базис Хаара связан при размерности матрицы равной, числу отсчётов, с тем, что интерполированный сигнал в точности совпадает с исходной системой отсчетов. Однако при этом мы всё же получаем ценные данные о компонентном составе сигнала в виде набора коэффициентов разложения по базисным функциям. Тем самым открывается возможность использовать качественные меры различия сигналов, такие, как χ2 – расстояние, расстояние Махалонобиса, спектральное расстояние [5], которые в перспективе позволяют построить качественные шкалы «тяжести» патологических изменений состояний костной ткани.
Применение системы ортогональных функций Хаара для анализа сигналов ФБМП
Обработка сигналов, полученных в результате ФБМП, проводилась по n = 16 точкам с соответствующими размерами матриц в выражениях (7), (8), (9), (10).
Анализ результата исследования по методу ФБМП для лучевой кости руки человека проводился с целью выделения механической и функциональной составляющей ответа. При этом для визуально выделенного информативного участка сигнала, который представлял собой механическую часть ответа, были оценены коэффициенты разложения по формуле (2) по 16 точкам. Аналогично были оценены коэффициенты разложения для следующего (функционального) участка сигнала. Результаты вычислений приведены в табл. 1.
Таблица 1
Оценка различия коэффициентов разложения по базису Хаара для двух последовательных участков сигнала

Различия между значениями коэффициентов разложения находятся в интервале от 50 % до 433 %, что является весьма существенным. Выраженный «пороговый» характер позволяет использовать эти различия в качестве информативного признака разделения механической и функциональной части ответа на тестовое воздействие.
Также представлял интерес анализ чувствительности коэффициентов разложения к некоторым характерным изменениям в механическом и функциональном состоянии кости. Для исследования этого факта реализовали измерение с механической нагрузкой на кость по типу «сдавливания». Результаты вычислений коэффициентов и их сравнения приведены в табл. 2.
Таблица 2
Результаты разложения по функциям Хаара для ФБМП без нагрузки и с нагрузкой, а также оценка различия в коэффициентах разложения

Наибольшее различие наблюдается в правой части таблицы, соответствующей более «коротким», «высокочастотным» компонентам разложения. Очевидно, что используемый тип нагрузки привел к уменьшению амплитуды «высокочастотной» составляющей ответа, что и нашло отражение в распределении коэффициентов. Очевидно, аналогичные изменения в первую очередь в «высокочастотной» части разложения будут проявляться и при более сильных, например, повреждающих, изменениях кости вплоть до переломов. Такое поведение коэффициентов может служить диагностическим признаком наличия повреждений и степени их выраженности, например, при сравнении поврежденной и интактной костей.
Выводы
Таким образом, использование системы ортогональных функций Хаара для обработки биомеханических сигналов позволяет исследовать основные свойства таких сигналов. Отличительная особенностью применения такой системы заключается в том, что она легко представима в матричной форме, что повышает удобство применения, в том числе во встраиваемых системах. Использование системы ортогональных функций Хаара для компонентного анализа результатов измерений позволяется построить методику, алгоритмическая сложность которой растет линейно в зависимости от объема массива данных. Кроме того, полученные коэффициенты разложения удобны для качественного анализа и интерпретации результатов врачом клиницистом. Предложенная методика, как показали предварительные исследования, позволяет устанавливать простые связи характера изменения коэффициентов разложения с типовыми патологическими изменениями в костной ткани.
Рецензенты:
Васильев В.И., д.т.н., профессор, заведующий кафедрой вычислительной техники и защиты информации, ФГБОУ ВПО «Уфимский государственный авиационный технический университет» Министерства образования и науки РФ, г. Уфа;
Куликов Г.Г., д.т.н., профессор, заведующий кафедрой «Автоматизированные системы, управления» ФГБОУ ВПО «Уфимский государственный авиационный технический университет» Министерства образования РФ, г. Уфа.
Работа поступила в редакцию 24.06.2014.



