При производстве минераловатной продукции актуальной является задача оценки дебита струи расплава плавильного агрегата. Решение этой проблемы возможно благодаря использованию системы контроля на основе технического зрения: камера снимает непосредственно процесс вытекания струи расплава из плавильного агрегата, передавая получаемую информацию в виде потока видеокадров в режиме телевизионного стандарта на вычислительное устройство для анализа. Выбор указанного подхода к реализации архитектуры системы влечет за собой необходимость решения типичной для систем технического зрения задачи – срыва слежения за объектом.
В данной задаче объектом слежения является изображение струи расплава в пределах телевизионного кадра. На производстве часто возникает ситуация, когда равномерное истечение струи нарушается вследствие засорения выходного отверстия плавильного агрегата, и струя уходит из поля зрения видеокамеры. Задачу отслеживания траектории движения струи расплава предлагается решать посредством включения в состав аппаратно-программного комплекса по оценке дебита струи расплава следящей системы, управляющей перемещением видеокамеры в соответствии с траекторией движения струи.
Полное математическое описание системы является сложной аналитической задачей, в связи с чем приемлемым и наглядным является использование метода динамического имитационного моделирования. Такое моделирование имеет целью отыскание оптимального закона регулирования, определение числовых значений, позволяющих системе управления достичь более высоких характеристик качества регулирования, и обоснование таких решений посредством проведения исследования и анализа полученных результатов. В данной работе построение модели следящей системы для комплекса по оценке дебита струи расплава осуществлялось с применением пакета модельно-ориентированного программирования Simulink.
Основная часть
Существенной особенностью проектируемой системы слежения является наличие в ее контурах информации как аналогового, так и цифрового вида (рис. 1).
Рис. 1. Структурная схема системы слежения
При этом необходимо обеспечивать требуемые показатели качества работы системы, а именно точность отработки входного воздействия, время переходного процесса, величину перерегулирования при отработке ступенчатого воздействия и ширину полосы пропускания.
В приведенной структурной схеме системы (рис. 1), построенной на основе предложенных в [5] рекомендаций, задающий сигнал θP – угловое направление на объект, выходной сигнал q – угол оптической оси видеокамеры, Δq – рассогласование. В качестве цифрового регулятора используется дискретный ПИД-регулятор с передаточной функцией вида
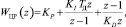(1)
где TД – период дискретизации; KP, KI KD – коэффициенты регулятора.
Передаточная функция интегратора реализована алгоритмом Эйлера. Оператор дифференцирования заменен конечной разностью. Замкнутый контур с цифровым регулятором работает на частоте дискретизации f = 1⁄TД.
В качестве исполнительного устройства в проектируемой модели следящей системы контроля местоположения изображения струи рассматривается механическая поворотная платформа, управляемая шаговым двигателем. Приближенное моделирование непрерывной части системы по данным видеонаблюдения выполнено на основе теоретических положений [2, 3], в результате чего определена ее переходная характеристика:
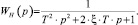(2)
Перед непрерывным звеном включен формирующий элемент. В предложенной схеме функции этого элемента выполняет фиксатор уровня нулевого порядка. Его передаточная функция имеет вид
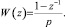(3)
Время запаздывания, обусловленное в реальной системе характеристиками канала связи и переходными процессами в двигателе, в модели описано элементом задержки.
В фиксированные моменты времени с периодом дискретизации TД управляющая программа сравнивает текущее положение струи расплава, приведенное к угловому положению вала двигателя, с угловым положением оптической оси видеодатчика. Значение TД определяется аналого-цифровым преобразователем (частотой замыкания ключа Кл1).
Кроме полезного задающего сигнала на входе следящей системы присутствует помеха, обусловленная погрешностью вычисления требуемого угла поворота платформы, которая зависит от характеристик видеодатчика (разрешение формируемого изображения, ширина поля зрения) и точности вычисления координат центра объекта применяемыми пространственно-временными алгоритмами. В данной модели полагается, что ошибки малы и ими пренебрегают.
Основным показателем качества работы системы является обеспечение отработки входного воздействия с минимальной ошибкой.
На основе метода, приведенного в [1], для того, чтобы заданное воздействие воспроизводилось с ошибкой не более emax, ЛАЧХ разомкнутой системы не должна заходить в область, ограниченную прямыми с наклонами –20 и –40 дБ. Для определения требований к низкочастотной части ЛАЧХ необходимо задать максимальное по модулю значение скорости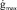 
, максимальное по модулю значение ускорения 
входного сигнала g(t) и максимально допустимую ошибку слежения emax. Моделирование системы осуществлялось для исходных данных, приведенных в табл. 1.
Поиск параметров ПИД-регулятора (оптимизация системы слежения), удовлетворяющих техническим условиям в частотной и временной областях, осуществлен с помощью пакета Simulink Response Optimization.
На рис. 2 представлены частотные характеристики проектируемой следящей системы для требуемых показателей точности работы.
а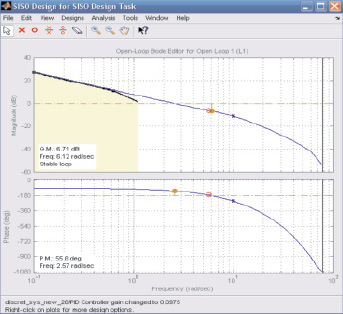 
б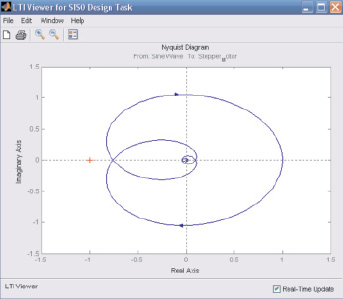 
Рис. 2. Частотные характеристики следящей системы: а – Диаграмма Боде:сверху – ЛАЧХ, снизу – ЛФЧХ; б – Диаграмма Найквиста (АФЧХ)
Таблица 1
Исходные данные
|
Параметр |
Значение |
|
Максимальная скорость входного воздействия, угл. град./с |
1 |
|
Максимальное ускорение входного воздействия, угл. град./с2 |
0,1 |
|
Максимально допустимая ошибка слежения emax, угл. град. |
3 |
|
Период дискретизации TД, с |
0,04 |
|
Время переходного процесса, с |
1,5 |
|
Величина перерегулирования не более, % |
20 |
Анализ полученных диаграмм Боде и диаграммы Найквиста позволяет сделать вывод о возможности достижения заданных показателей при построении системы слежения на основе предложенной модели (см. рис. 1). Частота среза wср системы (L(wср) = 0) располагается левее величины ωp, определяемой из соотношения j(ωp) = –p, что говорит о достаточном запасе устойчивости [4].
На рис. 3 приведены временные ограничения на ступенчатый входной сигнал для заданных параметров.
Выводы о достижимой точности работы системы можно судить по полученным данным моделирования, приведенным в табл. 2.
Таблица 2
Результаты моделирования
|
Параметр |
Значение |
|
Коэффициенты ПИ-регулятора, KP/KI/KD |
0,39/2,4/0,001 |
|
Перерегулирование, % |
10 % |
|
Запас по амплитуде, дБ |
6,71 |
|
Запас по фазе, град. |
55,8 |
|
Максимальная ошибка сопровождения, угл. град. |
3 |
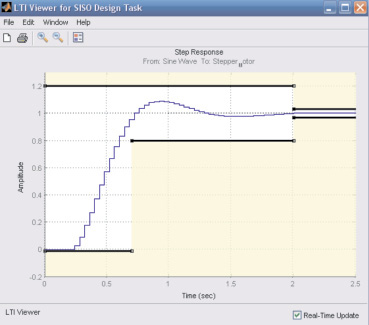
Рис. 3. Ограничения на ступенчатый входной сигнал
Определяющее влияние на качество и точность работы системы оказывают период дискретизации и задержка в передаче данных, обусловленная конечным временем команд управления и равная сумме задержек на отправку данных из последовательного порта, передачи их по каналу и прием данных в последовательный порт на приемной стороне. Частота поступления кадров видеоизображений определяет частоту дискретизации системы. Уменьшение периода дискретизации приведет к увеличению нагрузки на аппаратную часть системы, что нежелательно.
Заключение
В данной работе предложена математической модель системы слежения на основе электромеханического шагового двигателя. При помощи пакета моделирования Simulink произведена оптимизация его параметров. Проведен анализ устойчивости следящей системы с использованием критерия Найквиста, рассчитаны и построены временные и частотные характеристики. Результаты моделирования показали, что:
– величина перерегулирования не превышает допустимого показателя 10 %;
– найденные параметры модели (коэффициенты ПИД-регулятора) обеспечивают ошибку слежения 3 угл. град., время переходного процесса 1,5 с, что удовлетворяет требованиям к системе.
Таким образом, можно сделать вывод, что созданы все предпосылки для программной реализации цифрового управления шаговым двигателем для автоматического слежения за струей расплава на основе полученной модели.
Рецензенты:
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой «Информационные технологии», УрФУ, г. Екатеринбург;
Поршнев С.В., д.т.н., профессор, заведующий кафедрой «Радиоэлектроника информационных систем», УрФУ, г. Екатеринбург.
Работа поступила в редакцию 16.12.2013.