Из-за сложности решения дифференциальных уравнений, описывающих деформированное состояние оболочек вращения, большое распространение получили численные методы определения их напряженно-деформированного состояния. Среди численных методов особое место занимает метод конечных элементов (МКЭ) в различных формулировках: в формулировке метода перемещений разрабатывались конечные элементы в двумерной постановке [1, 6] и в трехмерной постановке [4]; в смешанной формулировке использовались объемные конечные элементы [2]. Объемные конечные элементы в формулировке метода перемещений успешно использовались для расчета слоистых конструкций [3, 5].
В настоящей работе объемный конечный элемент в форме шестигранника адаптирован к расчету сочлененных оболочек вращения.
Матрица жесткости объёмного шестигранного конечного элемента. Для расчета произвольно нагруженной оболочки вращения в координатной системе s, θ, ζ используется шестигранный восьмиузловой конечный элемент с узлами i, j, k, l на нижней грани по координате ζ и узлами m, n, p, h по верхней грани [4].
Используемая в настоящей работе матрица жесткости объёмного шестигранного конечного элемента, формируемая на основе равенства работ внешних и внутренних сил [3, 4, 5], представляется выражением
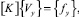 (1)
(1)
где 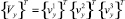 – вектор узловых неизвестных в криволинейной системе координат s, θ, ζ;
– вектор узловых неизвестных в криволинейной системе координат s, θ, ζ;
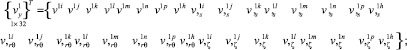
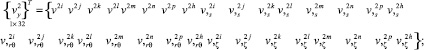

[K] – матрица жесткости элемента в глобальной системе координат; {f} – вектор узловых нагрузок элемента в глобальной системе координат.
Геометрия произвольно нагруженной оболочки вращения. Положение произвольной точки М срединной поверхности произвольно нагруженной оболочки вращения в декартовой системе координат xуz определяется радиус-вектором (рис. 1)
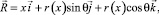 (2)
(2)
где i = r(x) – радиус вращения точки М относительно оси ox; 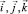 – орты декартовой системы координат; θ – угол, отсчитываемый от вертикального диаметра против часовой стрелки.
– орты декартовой системы координат; θ – угол, отсчитываемый от вертикального диаметра против часовой стрелки.
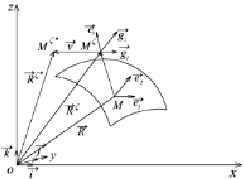
Рис. 1. Перемещение точки в результате деформирования оболочки из положения Mζ в положение Mζ*
Векторы локального базиса точки М определяются дифференцированием выражений (2)
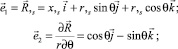
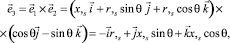 (3)
(3)
где r,s = r,xx,s – производная радиуса вращения по дуге меридиана s.
Производные векторов локального базиса определяются дифференцированием (3) и представляются в матричном виде
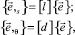 (4)
(4)
где
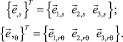
Радиус-вектор произвольной точки оболочки Mζ, отстоящей на расстоянии ζ от срединной поверхности, можно представить выражением
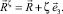 (5)
(5)
Базисные векторы точки Mζ определяются дифференцированием (5)
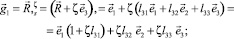
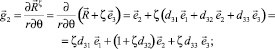 (6)
(6)
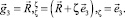 (7)
(7)
Произвольная точка Mζ оболочки под действием заданной нагрузки займет положение Mζ*, которое определяется вектором  с компонентами в базисе точки M срединной поверхности
с компонентами в базисе точки M срединной поверхности
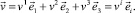 (8)
(8)
Производные вектора перемещения по координатам s, r, θ, ζ с учётом (4) имеют вид
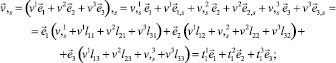
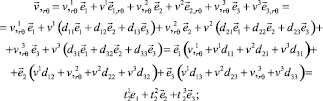
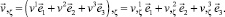 (9)
(9)
Геометрия в зоне пересечения произвольно нагруженных оболочек вращения из однородного материала. Рассматриваются две произвольно нагруженные оболочки вращения в координатах xyz и x′y′z′. Связь между ортами этих систем считается известной (рис. 2)
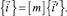 (10)
(10)
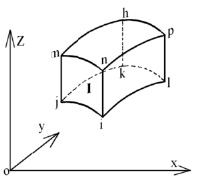
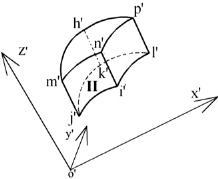
Рис. 2. Оболочки вращения в декартовых системах координат xoz и x′o′z′
На основании (10) определяется соотношение между векторами локальных базисов в граничной точке сочлененных оболочек
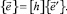 (11)
(11)
В узлах, расположенных в плоскости пересечения оболочек, узловые неизвестные одной оболочки (элемент I) принимаются за основные (рис. 2), узловые неизвестные примыкающей оболочки (элемент II) должны быть выражены через узловые неизвестные основной оболочки. В дальнейшем величины, относящиеся к примыкающей оболочке, будут отмечаться штрихами.
Для конечных элементов, примыкающих к плоскости сочленения оболочек, выполняются перенумерации неизвестных и рассматриваются следующие векторы узловых неизвестных для основной и примыкающей оболочек
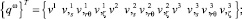 (12)
(12)
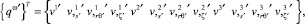 (13)
(13)
где
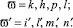
Соотношения между компонентами векторов(12) и (13) определяются с использованием следующих условий:
1. Векторы перемещений в точке, расположенной в плоскости пересечения двух оболочек, равны
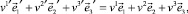
откуда с учётом (21) получается
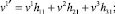
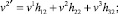
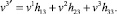 (14)
(14)
Зависимости между производными компонент вектора перемещений для двух оболочек на линии пересечения можно получить, используя выражения производной вектора по направлению
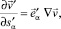 (15)
(15)
где
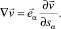
Используя (15), можно записать соотношения
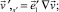 (16)
(16)
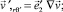 (17)
(17)
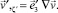 (18)
(18)
Равенство (16) с использованием (9) запишется в виде
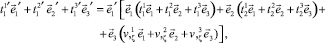
откуда получаются выражения
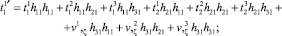
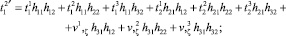
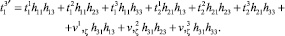 (19)
(19)
Используя выражение (9), можно выразить из (19) производные компонент вектора перемещений 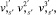 примыкающей оболочки через узловые неизвестные основной оболочки, например,
примыкающей оболочки через узловые неизвестные основной оболочки, например,
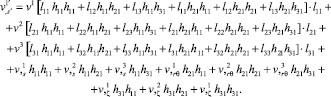 (20)
(20)
Аналогично из равенства (17), (18) с использованием (9), получая соответствующие выражения 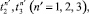 можно выразить
можно выразить
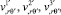
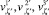 .
.
На основании полученных выражений зависимость между векторами (12) и (13) запишется матричным выражением
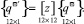 (21)
(21)
С использованием (21) формируется матрица [Т] для преобразования матриц жесткости и векторов узловых нагрузок конечных элементов, примыкающих к плоскости пересечения оболочек
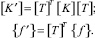 (22)
(22)
Пример расчета: Определялось напряженнo-деформированное состояние цилиндра с эллиптическим днищем, находящегося под действием давления интенсивности q (рис. 3). Цилиндр и эллиптическое днище из однородного материала.
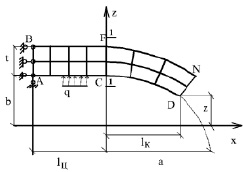
Рис. 3. Цилиндр с эллиптическим днищем, находящийся под действием давления интенсивности q
Были приняты следующие исходные данные: b = 0,2 м, i= 0,01 м, lц = 0,2 м, а = 0,4 м, lк = 0,392 м, z = 0,04 м, q = 1 Н, E = 2∙106 МПа, ν = 0,3.
По толщине цилиндр и эллиптическое днище разбивались на 2 равных дискретных элемента.
По длине цилиндр разбивалась на 10 одинаковых элементов, а эллиптическое днище – на 50 одинаковых элементов.
По полученным результатам построена эпюра нормальных напряжений σss в сечении 1–1 (рис. 3).
Для контроля точности вычислений выполнена проверка 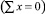 , которая дает ошибку:
, которая дает ошибку:
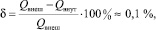
где 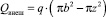 – равнодействующая внешних сил; Qвнутравнодействующая внутренних сил в сечении 1–1.
– равнодействующая внешних сил; Qвнутравнодействующая внутренних сил в сечении 1–1.
Результаты проверки свидетельствуют о корректности разработанного алгоритма расчета оболочек вращения в зоне соединения при произвольном нагружении.
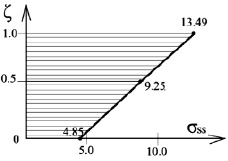
Рис. 4. Эпюра нормальных напряжений σss в сечении 1–1 цилиндра с эллиптическим днищем
Рецензенты:
Беликов Г.И., д.т.н., профессор кафедры «Сопротивление материалов», ФООГУ «Волгоградский архитектурный университет» Министерство образования и науки, г. Волгоград;
Ахмедов А.Д., д.т.н., профессор кафедры «Кадастр недвижимости и геодезии», ФГБОУ ВПО «Волгоградский государственный аграрный университет», г. Волгоград.
Работа поступила в редакцию 03.09.2013.



