На протяжении последнего десятилетия перед специалистами в различных сферах компьютерных технологий остро стоит проблема верификации программного обеспечения. Не обнаруженная на этапе разработки ошибка способна привести к катастрофическим последствиям. В некоторых прикладных областях невозможно своевременно остановить неправильно функционирующую программу, или ее остановка обойдется слишком дорого. Скрытые ошибки рано или поздно могут стать причиной огромных финансовых потерь и даже человеческих жертв, что подтверждает целый ряд примеров [1, 6].
К сожалению, даже самое глубокое тестирование не способно гарантировать корректности выполнения программы. Ситуация значительно усложняется при верификации параллельных процессов, так как в этом случае ошибки могут не проявляться до наступления специфических условий, связанных с их взаимодействием. И если корректность последовательной программы можно доказать, подав на вход всевозможные комбинации исходных данных и затем сравнив выходные данные с ожидаемыми, то для параллельной программы такой подход не дает оснований говорить об отсутствии ошибок. Кроме того, тестирование параллельных программ требует значительных временных затрат. В ряде случаев разработка тестов занимает на несколько порядков больше времени, чем разработка проверяемой программы.
В силу указанных причин в последнее время популярность приобретает формальный подход к верификации алгоритмов и программ, позволяющий однозначно ответить на вопрос корректности объекта анализа [3].
Одним из наиболее эффективных методов формальной проверки является техника model checking, включающая три элемента: способ построения модели исследуемого объекта, способ спецификации предъявляемых требований и способ проверки соответствия модели требованиям.
Применение логического выводадля решения задачи верификации
Удобным способом представления модели алгоритма (или программы) является структура Крипке, которая отличается простотой и высокой степенью универсальности [2]. Требования к объекту исследования могут быть описаны посредством формул темпоральной логики – расширения классической логики высказываний, позволяющего учитывать порядок событий во времени [1]. Именно эти элементы являются базовыми при выполнении первого и второго этапа формальной верификации с помощью техники model checking.
Классический подход предполагает, что сопоставление модели и спецификации может быть проведено на основе некоторых теорем и структур математического аппарата теории автоматов (сравнение реагирующего и контрольного автоматов Бюхи) [1]. Однако третий этап верификации возможно модифицировать следующим образом.
Ряд существующих методов логического вывода обладает высокой степенью параллелизма, что может быть использовано для ускорения процесса проверки соответствия модели предъявляемым требованиям [5]. Но в таком случае требуется решить задачу построения базы знаний, эквивалентной модели объекта верификации и представленной в форме, подходящей для обработки машиной логического вывода. Кроме того, необходим алгоритм преобразования спецификации в целевое утверждение, выводимость которого будет устанавливаться.
В нашем случае задача формирования базы знаний на языке логики предикатов первого порядка может быть решена с помощью следующего алгоритма.
1. Для установления связей между состояниями структуры и множеством атомарных предикатов введем двухместный предикат Event (α, β), который принимает истинное значение, если состояние структуры α отмечено атомарным предикатом β, и ложное в противном случае.
2. Для определения возможности перехода из одного состояния структуры в другое за один шаг введем двухместный предикат Parent (α, β), который принимает истинное значение, если из состояния α структуры Крипе существует ребро в состояние β.
3. Для определения отсутствия возможности перехода из вершины введем одноместный предикат End (α), который принимает истинное значение, если состояние α структуры Крипке не имеет исходящих дуг.
4. Для определения возможности перехода из одного состояния структуры в другое введем двухместный предикат Path (α, β), который принимает истинное значение, если из состояния α структуры Крипке существует путь в состояние β. Значение предиката для конкретных вершин структуры может быть вычислено через предыдущий как
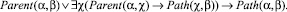
5. Дополнительно необходимо определить предикаты, отражающие требования к объекту верификации. Для этого следует построить дерево грамматического разбора заданной спецификации. Этот шаг может быть выполнен с помощью алгоритма, представленного в работе [4].
6. Последовательно, начиная с листьев дерева разбора, сопоставить каждой вершине отдельный предикат. Правила, по которым формируется сопоставляемый предикат, определяются логикой, используемой для описания требований к объекту верификации. Для спецификации в виде формулы темпоральной логики линейного времени (LTL) необходимо использовать следующий набор правил.
– Если вершина соответствует атомарному предикату, то сопоставить ей предикат вида Event (λ, χ) → Pi(λ), где Pi – вводимый предикат, а χ – атомарный предикат.
– Если вершина соответствует операции логического отрицания, то сопоставить ей предикат, получаемый как отрицание предиката-потомка данной вершины ⌐Pj(λ) → Pi(λ), где Pi – вводимый предикат, а Pj – предикат, введенный ранее при анализе потомка текущей вершины).
– Если вершина соответствует операции конъюнкции, то сопоставить ей предикат, получаемый с помощью конъюнкции предикатов-потомков данной вершины Pj(λ) ˄ Pk(λ) → Pi(λ), где Pi – вводимый предикат, а Pj и Pk – предикаты, введенные ранее при анализе потомков текущей вершины).
– Если вершина соответствует операции дизъюнкции, то сопоставить ей предикат, получаемый с помощью дизъюнкции предикатов-потомков данной вершины Pi(λ) ˅ Pk(λ) → Pi(λ), где Pi – вводимый предикат, а Pj и Pk – предикаты, введенные ранее при анализе потомков текущей вершины).
– Если вершина соответствует темпоральному оператору X, то сопоставить ей предикат вида
,
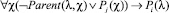где Pi – вводимый предикат, а Pj – предикат, введенный ранее при анализе потомка текущей вершины.
– Если вершина соответствует темпоральному оператору G, то сопоставить ей предикат вида
,
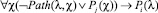где Pi – вводимый предикат, а Pj – предикат, введенный ранее при анализе потомка текущей вершины.
– Если вершина соответствует темпоральному оператору F, то сопоставить ей предикат вида
,
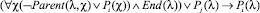где Pi – вводимый предикат, а Pj – предикат, введенный ранее при анализе потомка текущей вершины.
– Если вершина соответствует темпоральному оператору U, то сопоставить ей предикат вида
,
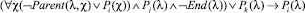где Pi – вводимый предикат, а Pj и Pk – предикаты, введенные ранее при анализе потомков текущей вершины.
– Если вершина соответствует темпоральному оператору W, то сопоставить ей предикат вида
,
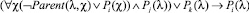где Pi – вводимый предикат, а Pj и Pk – предикаты, введенные ранее при анализе потомков текущей вершины.
– Если вершина соответствует темпоральному оператору R, то сопоставить ей предикат вида
,
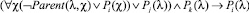где Pi – вводимый предикат, а Pj и Pk – предикаты, введенные ранее при анализе потомков текущей вершины.
Так как LTL-формула описывает желаемое поведение объекта верификации, то факт присутствия ошибки может быть подтвержден существованием в структуре Крипке последовательности состояний, нарушающей это поведение. Следовательно, выводимым утверждением будет являться отрицание предиката, сопоставленного корневой вершине дерева грамматического разбора анализируемой спецификации, для начального состояния модели.
Пример верификации с помощью ускоренного метода логического вывода
Рассмотрим процесс поиска ошибки на примере.
Пусть требуется проверить корректность алгоритма, состоящего из трех параллельно реализуемых процессов. Действия, совершаемые каждым из процессов, могут быть записаны на языке псевдокода следующим образом.
Основной процесс:
1: Загрузка данных // Загрузка из ВЗУ данных, необходимых для работы.
2: Инициализация вспомогательного процесса // Запуск процесса-обработчика запросов.
3: Инициализация семафора // Инициализация семафора, регулирующего доступ к данным.
Вспомогательный процесс:
1: Цикл (пока не получен сигнал завершения).
2: Если (есть успешная попытка успешного подключения), то // Если есть пользовательский запрос.
3: Инициализация процесса обработки данных // Запуск отдельного процесса, обрабатывающего пользовательский запрос.
4: Конец цикла // Метка не является командой.
Процесс обработки данных:
1: Захват семафора.
2: Обработка данных // Выполнение запроса пользователя, модификация данных.
3: Освобождение семафора.
Структуры Крипке, эквивалентные каждому из процессов, представлены на рис. 1.
Вершина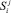 
соответствует команде с номером i j-го по порядку процесса, при этом 
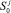и 
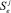соответствуют состояниям начала и завершения процесса. Множество атомарных предикатов состоит из двух элементов {α, β}, первый из которых соответствует операции инициализации семафора, а второй – операциям взаимодействия с семафором.
Асинхронная композиция структур Крипке представлена на рис. 2. Вершина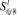 
соответствует объединению команд i, j, k и имеет порядковый идентификатор l. Следует заметить, что при построении данной композиции состояния 
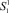и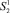 
первого процесса 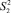и 
и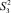 
второго были сжаты в одно состояние с меньшим номером. Кроме того, состояние 
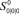соответствует моменту времени, когда ни один процесс не начал свою работу, а 
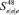– когда все процессы завершились.
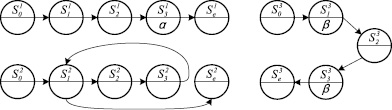
Рис. 1. Структуры Крипке отдельных процессов
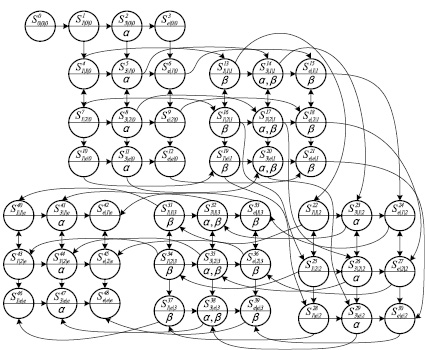
Рис. 2. Асинхронная композиция структур Крипке
Пусть необходимо проверить, удовлетворяет ли представленный алгоритм свойству: «Любому обращению к семафору предшествует операция его инициализации». Данное требование может быть перефразировано следующим образом: «Когда-либо в будущем выполнится операция инициализация семафора, а до тех пор не будет ни одного обращения к семафору, или же обращение к семафору не произойдет никогда». На языке темпоральной логики линейного времени свойство будет иметь вид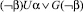 
.
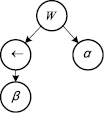
Рис. 3. Оптимизированное дерево грамматического разбора формулы темпоральной логики линейного времени
На этапе построения дерева грамматического разбора с помощью предложенного в работе [4] алгоритма к спецификации могут быть применены стандартные преобразования, после чего будет получена оптимизированная структура, представленная на рис. 3.
Использование предложенного выше алгоритма приведет к построению базы знаний, содержащей двести шестнадцать фактов. Ниже представлены факты, порождаемые вершинами композиции с порядковыми номерами 0–9 и 48. Остальные элементы имеют аналогичный вид.
1) 
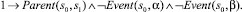
2) 
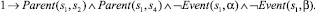
3) 
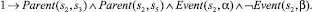
4) 
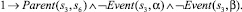
5) 
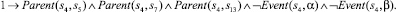
6) 
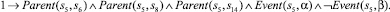
7) 
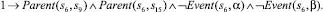
8) 
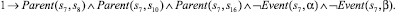
9) 
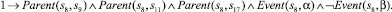
10) 
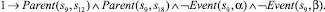
11) 
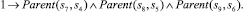
12) 
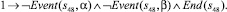
Кроме того, в результате анализа дерева разбора спецификации (с учетом необходимости проверки выводимости отрицания требования) в базу знаний будут добавлены следующие утверждения.
1) 
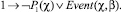
2) 
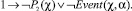
3) 
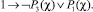
4) 
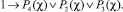
5) 
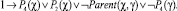
Выводимым утверждением в таком случае будет посылка вида 1 → P4(s0).
Применение метода деления дизъюнктов [5] позволит установить выводимость целевого утверждения за четыре итерации. Более того, найденная траектория вывода (s0 → s1 → s4 → s13) будет являться контрпримером – последовательностью состояний алгоритма, приводящей к нарушению спецификации. Анализ трассы показывает, что возможной является ситуация, когда из-за возникновения задержки после второй операции основного процесса (например, вследствие длительной инициализации нескольких обработчиков запросов) экземпляр третьего процесса попытается использовать непроинициализированный семафор. Последствия такой ситуации непредсказуемы, поэтому ее следует считать недопустимой.
Заключение
Таким образом, предлагаемый способ формирования базы знаний на основе структуры Крипке, эквивалентной исследуемому алгоритму, и спецификации, описывающей предъявляемые требования, позволяет использовать на заключительном этапе верификации математический аппарат теории логического вывода. Данное решение за счет высокой степени параллелизма этого аппарата позволяет значительно сократить общее время формальной проверки корректности алгоритмов и программ.
Асимптотическая сложность способа определяется как O(M + K), где M – число связей между состояниями модели (в большинстве случаев сравнимо с числом состояний модели), а K – число лексем спецификации. Кроме того, предлагаемый способ не зависит от конкретных методов логического вывода. Вследствие универсальности полученной базы знаний рекомендуемый к применению модифицированный ускоренный метод деления дизъюнктов может быть заменен любым подходящим методом, оперирующим знаниями в логике предикатов.
Представленный способ был использован при разработке программной системы для верификации параллельных алгоритмов с помощью ускоренного метода логического вывода.
Рецензенты:
Пономарев В.И., д.т.н., профессор, директор закрытого акционерного общества «НПП «Знак», г. Киров;
Вечтомов Е.М., д.ф.-м.н., профессор, зав. кафедрой «Алгебра и дискретная математика», ФГБОУ ВПО «ВятГГУ», г. Киров.
Работа поступила в редакцию 11.07.2013.