Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В наногетероструктурах InAlAs/InGaAs/InAlAs, выращенных на подложках фосфида индия, можно создать двумерные электроны с высокой концентрацией более 1012 см–2, высокой подвижностью, высокой дрейфовой скоростью насыщения при комнатной температуре [1–3]. Данные структуры широко применяются для создания СВЧ устройств [4, 5]. Частота работы такого прибора f = Vд.н./Lg определяется дрейфовой скоростью насыщения Vд.н. и длиной затвора Lg. При этом сейчас возможно создать транзисторы с длиной затвора Lg ~ 25 нм, что близко к предельно возможной. Поэтому для увеличения рабочей частоты необходимо увеличение дрейфовой скорости электронов. Это возможно либо выбором полупроводников для создания гетероструктур, либо определенной конструкцией квантовой ямы.

Решеточно-согласованные (изоморфные) с подложкой InP квантовые ямы InyAl1-yAs/InxGa1-xAs/InyAl1-yAs обладают высоким содержанием индия х = 0,53. В квантовых ямах AlyGa1-yAs/InxGa1-xAs на подложках GaAs содержание индия ограничено величиной х = 0,2 [6]. Увеличение содержания индия необходимо для уменьшения эффективной массы электронов, так как в InAs эффективная масса электронов меньше, чем в GaAs. Однако существуют причины, препятствующие уменьшению эффективной массы двумерных электронов в квантовой яме и увеличению электронной подвижности за счет увеличения содержания индия. Это различные механизмы рассеяния в сложных многослойных гетеросистемах [7]. Поэтому разработка конструкции квантовой ямы, например, содержания индия в квантовой яме, наличие вставок различного состава в яму и исследование их влияния на подвижность электронов в квантовой яме является актуальной задачей.

Можно изменять профиль дна зоны проводимости, то есть делать различные вставки в основную квантовую яму, например, узкие, туннельно-прозрачные барьеры [8, 9], что изменяет фононный спектр и электронную подвижность. А можно вставлять в основную квантовую яму узкие более глубокие квантовые ямы [10]. Введение InAs в квантовую яму, с одной стороны, увеличивает электронную подвижность m за счет ослабления межподзонного рассеяния электронов и уменьшения эффективной массы электронов т* в квантовой яме. С другой стороны, увеличение толщины вставленного слоя InAs ограничено критическим значением, превышение которого приводит к ухудшению качества вставки и всей активной области из-за образования дислокаций несоответствия.

В настоящей работе изучалось влияние вставок InAs различной толщины на подвижности электронов в согласованных по параметру решеток квантовых ямах In0,53Ga0,47As на подложках InP. Использовался эффект Шубникова–де Гааза квантовых осцилляций магнетосопротивления. Проводились расчеты зонных диаграмм структур, квантовых и транспортных подвижностей в подзонах размерного квантования.

Материалы и методы исследований

Для изучения влияния вставок в канал на подвижности носителей заряда в настоящей работе была использована серия из 4-х образцов с изоморфной к подложке InP квантовой ямой In0,53Ga0,47As со вставками InAs различной толщины в центр ямы. Структура слоёв образцов схематически изображена на рис. 1. Образцы 2 и 3, в отличие от образца 1, содержат вставку InAs в квантовой яме, квантовая яма образца 4 состоит только из InAs. Образцы 1–3 дельта-легированы кремнием с двух сторон, образец 4 – с одной стороны.

Рис. 1. Структура слоёв образцов (серым выделена квантовая яма)

В табл. 1 приведены некоторые параметры образцов, а именно толщина слоя InAs d, концентрация NHall и подвижность μHall, полученные из эффекта Холла при 4,2 К и концентрации электронов NSdH в двух подзонах размерного квантования, полученные из эффекта Шубникова–де Гааза.

Таблица 1

Толщина слоя InAs d в центре квантовой ямы шириной L, концентрация NHall и подвижность μHall, полученные из эффекта Холла при 4,2 К и из эффекта Шубникова – де Гааза NSdH в двух подзонах

У всех образцов были исследованы температурные зависимости сопротивления в интервале температур 4,2–300 К, эффект Холла и эффект Шубникова–де Гааза при температуре 4,2 К в магнитных полях до 6 Тл, создаваемых сверхпроводящим соленоидом.

Результаты исследований и их обсуждение

На рис. 2 представлены зависимости сопротивления на квадрат от температуры ρxx(T) для исследованных образцов. При понижении температуры сопротивление уменьшается и показывает преимущественное рассеяние электронов на акустических фононах в этой области температур. При низких температурах рассеяние на фононах сменяется рассеянием на ионизированных примесях.

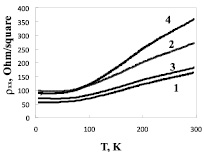
Рис. 2. Зависимости сопротивления на квадрат ρxx(T) от температуры для исследованных образцов. Цифры у кривых соответствуют номерам образцов в таблице 1

Во всех образцах при Т = 4,2 К наблюдались осцилляции магнетосопротивления (эффект Шубникова–де Гааза) В качестве примера на рис. 3 приведены осцилляции Шубникова–де Гааза, их Фурье-спектры и осцилляции холловского сопротивления для образца 1.

По графикам зависимостей сопротивления ρxx(B) от магнитной индукции B видно, что у данных структур (кроме образца 4) наблюдаются две частоты Шубникова–де Гааза, то есть заполнены две подзоны размерного квантования. Были определены частоты и по ним концентрации электронов NSdH (см. табл. 1). По зависимостям холловского сопротивления от магнитной индукции ρxy(B) были рассчитаны холловские концентрации NHall и подвижности μHall двумерных электронов. Эти величины также приведены в табл. 1, из которой видно, что сумма концентраций электронов в первой и второй подзонах, полученных из эффекта Шубникова–де Гааза, и концентрации, полученной из эффекта Холла, совпадают для всех образцов. Значение подвижности электронов у структуры с более широкой вставкой увеличилось по сравнению со значением подвижности у структуры без вставки и с узкой вставкой InAs. Подвижности электронов у образца с квантовой ямой (состоящей только из InAs) и образца с квантовой ямой InGaAs без вставки близки. То есть подвижность носителей заряда зависит от ширины вставки в квантовой яме, и она максимальна для вставки InAs шириной 31,4 Å.

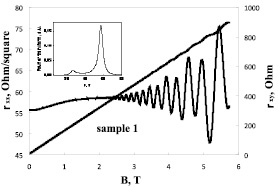
Рис. 3. Зависимость магнетосопротивления ρxx(B), холловского сопротивления ρxy(B) от магнитного поля B, Фурье-спектр осцилляций (вставка).

Расчёт зонной структуры, волновых функций, квантовой и транспортной подвижностей электронов

Методом самосогласованного решения уравнения Шрёдингера и уравнения Пуассона в приближении эффективной массы были получены профиль дна зоны проводимости, уровни энергии и волновые функции электронов. Метод расчёта и используемые параметры приведены в работах [11–13]. На рис. 4 представлены результаты расчётов для образца 3 с оптимальной шириной центральной вставки InAs. Как видно из рис. 4, действительно ниже уровня Ферми в квантовой яме находится два уровня размерного квантования. Наличие центральной вставки InAs в квантовую яму приводит к тому, что уровень размерного квантования E1 опускается ближе ко дну квантовой ямы. Он в основном формируется вставкой. Эффективная ширина квантовой ямы, определяемая полушириной волновой функции, уменьшается. Расстояние между первым E1 и вторым E2 уровнями энергии возрастает. Это приводит к увеличению электронной подвижности за счет ослабления межподзонного рассеяния. В то же время возрастает рассеяние на неоднородностях бокового рельефа, что несколько понижает подвижность. Но в целом при оптимальной толщине вставки подвижность электронов возрастает. Вставка InAs сжата по сравнению с изоморфными слоями In0.53Ga0.47As. Существует предельная ширина такой вставки, выше которой появятся дефекты. Как видно из табл. 1, максимальная электронная подвижность наблюдается в образце 3 со вставкой InAs в квантовой яме шириной 31,4 Å.

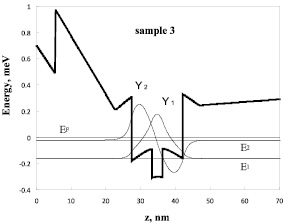
Рис. 4. Профиль дна зоны проводимости, уровни энергии и волновые функции электронов для образца 3. Энергия отсчитывается от уровня Ферми EF, E1 и E2 – уровни размерного квантования

Одним из важных методов изучения механизмов рассеяния электронов в квантовых ямах является исследование транспортного tt и квантового tq времен рассеяния электронов или квантовой 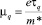и транспортной 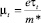подвижностей электронов [11–13]. Обе подвижности могут быть найдены либо из осцилляционной зависимости продольного магнетосопротивления в квантующем магнитном поле – эффекта Шубникова–де Гааза, либо прямыми расчетами [11–13]. При этом отношение μt/μq позволяет определить доминирующий характер рассеяния, определяющий электронную подвижность в квантовой яме. В одиночной квантовой яме AlGaAs/GaAs преобладает малоугловое рассеяние и μt/μq ~ 10 – 100. В гетероструктурах InAlAs/InGaAs на подложках InP, в основном, преобладает рассеяние на флуктуациях состава сплава и обычно μt/μq ≥ 1.

Транспортную подвижность можно рассчитать в рамках кинетического уравнения, рассматривая рассеяние на примесях в борновском приближении. Для нескольких заполненных подзон теория обобщена в [14] (см. также ссылки [11–13]). Результаты расчетов представлены в табл. 2. Как видно из сравнения обеих подвижностей, транспортная подвижность существенно превышает квантовую, что свидетельствует о преобладающем характере малоуглового рассеяния, характерного для рассеяния электронов на ионизированной примеси. Как видно из рис. 4, это связано с тем, что волновые функции электронов заходят в дельта слои легирующего кремния. Вторая особенность – расчетные подвижности превышают наблюдаемые экспериментально. Это в первую очередь связано с тем, что в расчетах не учтены дополнительные механизмы рассечяния в структурах со вставками, например рассеяние на латеральных неоднородностях.

Таблица 2

Квантовая μq и транспортная μt подвижности для первой и второй подзон размерного квантования

Заключение

В работе были исследованы электронные подвижности в изоморфных квантовых ямах In0.53Ga0.47As с центральной вставкой InAs различной толщины на подложках InP. Максимальная подвижность электронов наблюдается при ширине вставки d = 31,4 Å. Измерены и рассчитаны подвижности электронов в подзонах размерного квантования. Показано, что рассеяние на ионизированных примесях играет существенную роль в исследованных структурах.

Авторы благодарят Г.Б. Галиева, Е.А. Климова и И.С. Васильевского за предоставление образцов.

Рецензенты:

Константинова Е.А., д.ф.-м.н., профессор кафедры общей физики и молекулярной электроники физического факультета МГУ имени М.В. Ломоносова, г. Москва;

Скипетров Е.П., д.ф.-м.н., профессор кафедры физики низких температур и сверхпроводимости физического факультета МГУ имени М.В. Ломоносова, г. Москва.

Работа поступила в редакцию 22.02.2013.