Анализ современных рассеивателей электромагнитных волн показывает, что они в большинстве случаев имеют сложную структуру. Анализ и синтез таких объектов необходимо проводить с использованием моделей и методов, дающих, по возможности, меньшие ошибки.

В настоящее время при исследовании и разработке электродинамических объектов все чаще используют системы автоматизированного проектирования (САПР), что позволяет ставить и решать различные задачи теории дифракции электромагнитных волн (ЭМВ) на структурах сложной формы.

При решении задач дифракции радиоволн и проектировании объектов во многих случаях исследуют ограничения, накладываемые на средние характеристики рассеяния [1, 7].

В данной статье рассмотрены двумерные модели рассеяния электромагнитных волн, поскольку в ряде случаев трехмерные задачи могут быть сведены к двумерным.

Целью данной работы исследование возможности применения приближенных моделей для оценки средних характеристик рассеяния объектов и разработка предложений по структуре подсистемы САПР проектирования объектов с необходимыми средними характеристиками рассеяния.

Рассмотрим рассеяние ЭМВ на двумерном идеально проводящем цилиндре (рис. 1).

Для оценки средних характеристик такой структуры можно воспользоваться моделью цилиндра с параллельными боковыми стенками (рис. 2).

Необходимо оценить сектор углов наблюдения, отсчитываемый от нормали к боковой стороне цилиндра, в котором применима указанная модель цилиндра. Мы стремились к тому, чтобы различие в средних эффективных площадях рассеяния (ЭПР) цилиндра и его модели не превышало 3 дБ.

Интегральное уравнение Фредгольма первого рода для плотности неизвестного электрического тока в случае Е-поляризации [4] представляется в следующем виде:

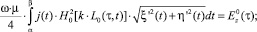
α ≤ τ ≤ β, (1)

где

–

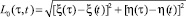расстояние от точки наблюдения до точки интегрирования; 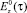– продольная составляющая напряженности первичного электрического поля в точке на контуре. Контур объекта задается в параметрической форме: x = ξ(t), y = η(t), α ≤ τ ≤ β, а ξ′(t), η′(t) – первые производные соответствующих функций, 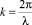, λ – длина падающей электромагнитной волны.

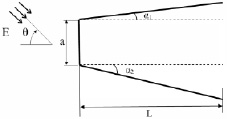
Рис. 1. Геометрия рассеяния ЭМВ на двумерном цилиндре:a, L – характерные размеры, α1, α2 – углы наклона боковых стенок; Е – вектор падающей электромагнитной волны; q – угол падения плоской ЭМВ

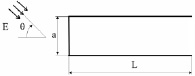
Рис. 2. Геометрия рассеяния ЭМВ на двумерном цилиндре:a, L – размер сторон цилиндра; Е – вектор падающей электромагнитной волны; q – угол падения плоской ЭМВ

Уравнение (1) решалось с использованием метода моментов.

Проводим расчет средней ЭПР на основе следующего выражения:

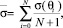(2)

где σ(θi) – величина ЭПР для угла наблюдения θi.

Введем величину a = max(a1, a2), которая дает максимальный угол наклона боковых стенок. Углы отсчитываются от нормали к боковой стенке.

На рис. 3 приведен пример расчета – линии уровня для возможных секторов углов наблюдения Dq в зависимости от a и L при a = 5°. С увеличением a сектор возможных углов наблюдения Dq будет уменьшаться. Подобные зависимости могут быть построены для других значений a.

В [5] решалась задача о возможности использования приближенной модели для полой структуры, аналогичным образом определялся сектор углов наблюдения, в [6] проводилось построение алгоритма для определения размеров полых структур с максимальными значениями средних характеристик рассеяния.

Таким образом, полученные зависимости размеров секторов углов наблюдения для приближенных моделей могут храниться в БД и далее передаваться в подсистему САПР средних характеристик объектов.

Описание процесса функционирования подсистемы САПР

Объект сложной формы можно представить в виде совокупности отдельных компонентов (цилиндров, полых структур и т.д.). Для определения характеристик компонентов воспользуемся коэффициентами корреляции. В качестве входных параметров выделим следующие:

1) вид компонента;

2) сектор углов наблюдения;

3) требуемый уровень для средних характеристик рассеяния.

Процесс функционирования подсистемы САПР расчета компонентов объекта приведен на рис. 4.

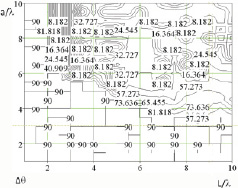
Рис. 3. Результаты определения секторов углов наблюдения Dq, в которых возможно представление исходной структуры (рис. 1) ее приближенной моделью (рис. 2)

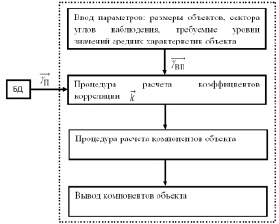
Рис. 4. Процесс функционирования подсистемы САПР средних характеристик объекта

Выходным результатом являются значения характеристик компонентов объекта.

Алгоритм работы в подсистеме будет следующий:

1. Ввод входных параметров.

2. Рассчитываются коэффициенты корреляции для каждого вида объекта.

3. На основе принципа максимума коэффициента корреляции выбирается наиболее подходящий компонент.

4. Вывод результата.

Использованы следующие обозначения: 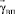– вектор, каждым из элементов которого являются соответствующие входные параметры; 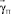– вектор, содержащий соответствующие зависимости в БД; 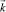– вектор, содержащий коэффициент корреляции [2, 3].

Процесс определения характеристик компонент сводится к выполнению следующей процедуры отыскания максимума коэффициента корреляции.

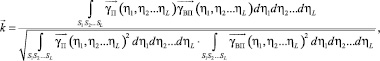(3)

где S1, S2, ..., SL – области изменения параметров (η1, η2, ..., ηL).

Для вектора коэффициентов корреляции с помощью стандартной процедуры находятся максимальные элементы, номера которых соответствуют требуемым компонентам, в соответствии с входными параметрами.

Заключение

Таким образом, рассмотренный в работе подход и полученные результаты могут быть полезны при проектировании объектов с заданными требованиями на средние характеристики рассеяния.

Рецензенты:

Кострова В.Н., д.т.н., профессор, проректор по мониторингу Воронежского института высоких технологий, г. Воронеж;

Чопоров О.Н., д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.

Работа поступила в редакцию 07.03.2013.