В последнее время высокопроизводительные вычислительные технологии развиваются необычайно высокими темпами. Причиной этого является появление все новых вычислительных задач, причем требования, предъявляемые этими задачами к методам и средствам их решения, постоянно ужесточаются. Одним из таких требований является необходимость обеспечения высокой вычислительной точности. Многопроцессорная многоядерная архитектура высокопроизводительных систем обуславливает актуальность разработок, направленных на создание методов и алгоритмов, позволяющих выполнять высокоточные вычислительные операции с распараллеливанием до уровня отдельных разрядов операндов. В этой области бесспорными преимуществами обладают методы, основанные на представлении числовых данных в системе остаточных классов (СОК).
1. Представление чисел в системе остаточных классов
Пусть задан ряд натуральных попарно взаимно простых чисел p1, p2, ..., pn. Тогда для любых целых x1, x2, ..., xn, таких, что 0 ≤ xi < pi существует целое X ∈ [0, P – 1], которое при делении на pi дает остаток xi для всех i = 1, 2, …, n, где 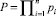 (китайская теорема об остатках [3]). Сказанное означает, что между прямым произведением колец
(китайская теорема об остатках [3]). Сказанное означает, что между прямым произведением колец 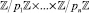 и кольцом
и кольцом 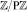 существует биективное отображение
существует биективное отображение 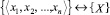 . Кортеж ⟨x1, x2, ..., xn⟩ определяется решением сравнений
. Кортеж ⟨x1, x2, ..., xn⟩ определяется решением сравнений 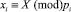 для всех i = 1, 2, …, n. Зададим последовательность чисел B1, B2, ..., Bn, таких, что
для всех i = 1, 2, …, n. Зададим последовательность чисел B1, B2, ..., Bn, таких, что 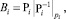 где
где 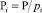 , а
, а 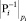 – мультипликативная инверсия от Pi по модулю pi. Тогда отображение
– мультипликативная инверсия от Pi по модулю pi. Тогда отображение 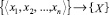 определится следующим образом:
определится следующим образом:
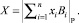 (1)
(1)
Тем самым на основе чисел p1, p2, ..., pn определяется система остаточных классов (СОК, Residue Number System) [1, 6] с полным диапазоном P и ортогональными базисами B1, B2, ..., Bn. Порождающие числа p1, p2, ..., pn называются основаниями (модулями) СОК. Вычеты xi в выражении (1) называют модулярными разрядами, а образованный ими кортеж – модулярным числом. Модулярное число будем обозначать следующим образом [6]:
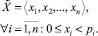 (2)
(2)
В СОК определены основные арифметические операции, которые делятся на две группы:
1. Модульные операции, к которым относятся арифметическое сложение, умножение, поразрядное сравнение модулярных чисел и т.д.
2. Немодульные операции, которые включают сравнение, вычитание модулярных чисел с возможностью получения отрицательного результата, контроль переполнения, округление (частный случай – масштабирование), деление и т.д.
Важнейшим преимуществом СОК является возможность параллельного выполнения модульных операций по всем разрядам операндов. Например, если даны 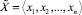 ,
, 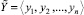 и необходимо получить
и необходимо получить 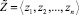 , такой, что
, такой, что 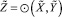 , то функция
, то функция 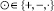 , отвечающая модульной операции, естественным образом представляется в виде декомпозиции более простых функций
, отвечающая модульной операции, естественным образом представляется в виде декомпозиции более простых функций 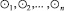 , таких, что
, таких, что 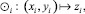 т.е. каждый разряд результата является функцией разрядов мантисс операндов по соответствующему основанию и не зависит от остальных разрядов.
т.е. каждый разряд результата является функцией разрядов мантисс операндов по соответствующему основанию и не зависит от остальных разрядов.
Основные недостатки СОК связаны с неочевидностью выполнения немодульных операций. В отличие от модульных, немодульные операции требуют знания величины модулярных чисел в целом. Значение каждой цифры результата немодульной операции не является функцией значений соответствующих цифр операндов, а зависит от значений этих операндов в целом, что обуславливает сложность выполнения таких операций.
2. Выполнение немодульных операций в СОК на основе приближенных позиционных характеристик
В основе алгоритмов выполнения немодульных операций лежат методы вычислений позиционных характеристик модулярных чисел [5]. Под позиционной характеристикой принято понимать выраженную тем или иным образом информацию о позиционном значении модулярного числа (2). Известны точные позиционные характеристики: ранг, след, коэффициенты обобщенной позиционной системы, диагональ и т.д. [1, 6]. Однако методы их вычисления характеризуются высокой вычислительной сложностью либо требуют больших аппаратурных затрат для хранения подстановочных данных. Поэтому полезной альтернативой точных является приближенный метод выполнения немодульных операций, предложенный Н.И. Червяковым и его коллегами в работах [4, 5]. Данный метод основан на вычислении приближенной позиционной характеристики, которая представляет собой округленное значение отношения модулярного числа к полному диапазону СОК [4, 5]:
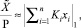 (3)
(3)
где 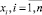 – разряды модулярного числа
– разряды модулярного числа 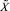 ,
, 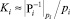 – константы, вычисляемые заранее и округленные в пределах разрядности вычислительного устройства,
– константы, вычисляемые заранее и округленные в пределах разрядности вычислительного устройства, 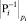 – мультипликативная инверсия от
– мультипликативная инверсия от 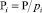 ,
,  – дробная часть аргумента. В работе [5] определен ряд простых правил применения приближенных позиционных характеристик для выполнения таких операций, как определение знака, сравнение, обнаружение ошибки и переполнения модулярных чисел, локализации ошибочного разряда.
– дробная часть аргумента. В работе [5] определен ряд простых правил применения приближенных позиционных характеристик для выполнения таких операций, как определение знака, сравнение, обнаружение ошибки и переполнения модулярных чисел, локализации ошибочного разряда.
Главным преимуществом приближенного метода выполнения немодульных операций в СОК является его низкая вычислительная сложность, порядка О(n) по количеству модулей (для последовательного алгоритма), в то время как точные методы либо требуют выполнения n2 и более операций, либо вызывают необходимость хранения подстановочных таблиц больших объемов. Например, при известных приближенных характеристиках правило сравнения чисел 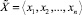 и
и 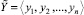 состоит в анализе условий [5]:
состоит в анализе условий [5]:
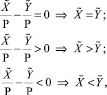
т.е. операция сравнения чисел в СОК сводится к вычислению приближенных позиционных характеристик по формуле (3) и их сопоставлению как обычных дробных чисел, представленных в одном из аппаратно поддерживаемых форматов данных. Вместе с тем, эта же операция при использовании, например, метода потактового перехода к полиадическому коду требует в предельном случае выполнения 2n тактов, каждый i-й из которых состоит из 2n – i операций над модулярными разрядами сравниваемых чисел.
Основные трудности, возникающие на пути эффективного использования приближенного метода, связаны с образованием существенных погрешностей округления при вычислении позиционной характеристики по формуле (3). Данные погрешности могут приводить к некорректному выполнению немодульных операций над модулярными числами.
Пример. Пусть p1 = 7, p2 = 9, p3 = 11, p4 = 13 – модули СОК, P = 9009 – их произведение. Для данных модулей константы Ki из формулы (3) определятся следующим образом: K1 ≈ 0,86, K2 ≈ 0,56, K3 ≈ 0,82, K4 ≈ 0,77. Число разрядов для представления констант выбиралось в соответствии с числом разрядов, необходимых для представления модулей СОК. Пусть 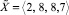 ,
, 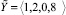 – модулярные числа, которые необходимо сравнить по величине.В соответствии с формулой (3) имеем:
– модулярные числа, которые необходимо сравнить по величине.В соответствии с формулой (3) имеем: 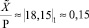 ,
, 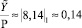 . Таким образом, будет сделан вывод, что
. Таким образом, будет сделан вывод, что 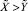 . Однако это заключение не соответствует истине. Действительно, преобразуя числа
. Однако это заключение не соответствует истине. Действительно, преобразуя числа 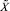 и
и 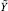 к целочисленному представлению по формуле (1), получим:
к целочисленному представлению по формуле (1), получим:
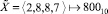 ;
;
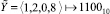 . □
. □
В рассмотренном примере показана ситуация, когда ошибки округления привели к существенной относительной погрешности при вычислении приближенной характеристики модулярного числа 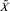 : точное ее значение равно ≈ 0,089, следовательно,
: точное ее значение равно ≈ 0,089, следовательно, 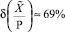 . Такое значение погрешности указывает на то, что приближенная позиционная характеристика не содержит ни одного верного разряда, что и привело в итоге к неверному заключению о результате сравнения чисел
. Такое значение погрешности указывает на то, что приближенная позиционная характеристика не содержит ни одного верного разряда, что и привело в итоге к неверному заключению о результате сравнения чисел 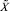 и
и 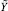 . При этом модулярный код числа
. При этом модулярный код числа 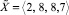 не указывает явно на возможность появления такой существенной погрешности, вследствие чего верифицировать корректность операции сравнения
не указывает явно на возможность появления такой существенной погрешности, вследствие чего верифицировать корректность операции сравнения 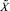 и
и 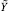 , как, впрочем, и любой другой немодульной операции, выполняемой с использованием приближенных позиционных характеристик, не представляется возможным.
, как, впрочем, и любой другой немодульной операции, выполняемой с использованием приближенных позиционных характеристик, не представляется возможным.
Таким образом, актуальной задачей является уменьшение погрешностей округления при вычислении приближенной позиционной характеристики.
3. Способ уточненного вычисления приближенной позиционной характеристики модулярного числа
Оценим погрешности, свойственные приближенной позиционной характеристике модулярного числа, вычисленной по формуле (3) с учетом округлений. Пусть в СОК с модулями p1, p2, ..., pn и полным диапазоном P = p1∙p2∙...∙pn задано модулярное число 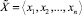 . Пусть
. Пусть 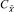 – точное значение отношения
– точное значение отношения 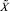 к P, определяемое, в соответствии с китайской теоремой об остатках, следующим образом:
к P, определяемое, в соответствии с китайской теоремой об остатках, следующим образом:
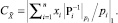 (4)
(4)
Здесь предполагается, что все слагаемые представленной суммы определяются точно (без округлений). Представим отношение мультипликативной инверсии от Pi к модулю pi в виде:
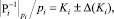
где Ki – константа СОК из формулы (3), вычисленная с конечной точностью представления, а Δ(Ki) – ее абсолютная погрешность округления. Тогда, воспользовавшись законами распространения абсолютных ошибок при умножении [2], получим:
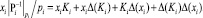 ,
,
где x1, x2, ..., xn – модулярные разряды числа 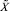 . Так как
. Так как 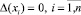 , то
, то
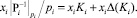
Известно, что максимальная абсолютная погрешность алгебраической суммы приближенных чисел равна сумме абсолютных погрешностей слагаемых, поэтому
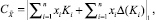
где 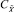 определяется по формуле (4).
определяется по формуле (4).
Следовательно, если приближенная позиционная характеристика определяется по формуле (3), то абсолютная и относительная погрешности будут ограничены неравенствами
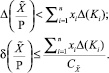
Заключаем таким образом, что погрешности, возникающие при определении приближенной позиционной характеристики по формуле (3), существенным образом зависят от суммы x1 + x2 + ... + xn значений разрядов модулярного числа 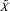 . Пусть двоичное представление всех констант Ki состоит из k разрядов, причем под дробную часть отведено k – 1 разрядов. Если все модули СОК p1, p2, ..., pn состоят также из k разрядов, то при округлении «до ближайшего»
. Пусть двоичное представление всех констант Ki состоит из k разрядов, причем под дробную часть отведено k – 1 разрядов. Если все модули СОК p1, p2, ..., pn состоят также из k разрядов, то при округлении «до ближайшего» 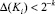 . Следовательно,
. Следовательно,
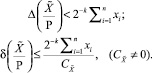 (5)
(5)
Способом уменьшения погрешностей (5) является изменение порядка арифметических действий при вычислении приближенной позиционной характеристики с ограниченной точностью по формуле (4): вначале следует вычислить произведение 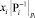 , а уже потом поделить его на модуль pi. Это позволит избежать накопления погрешностей при умножении округленного числа на соответствующий модулярный разряд. Обозначим
, а уже потом поделить его на модуль pi. Это позволит избежать накопления погрешностей при умножении округленного числа на соответствующий модулярный разряд. Обозначим 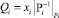 и выполним его разложение: Qi = Si pi + Ni для всех i = 1, 2, …, n. Здесь Ni является остатком от деления Qi на основание СОК pi, т.е.
и выполним его разложение: Qi = Si pi + Ni для всех i = 1, 2, …, n. Здесь Ni является остатком от деления Qi на основание СОК pi, т.е.
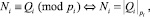
тогда формула (5) перепишется в следующем виде:
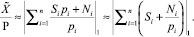
Целой частью Si каждого слагаемого в данной сумме можно пренебречь, что позволит работать в пределах разрядности модулей СОК. Таким образом, получается уточненная формула для определения приближенной позиционной характеристики модулярного числа:
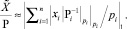 (6)
(6)
Погрешность каждого слагаемого в представленной сумме не зависит прямым образом от значений знакопозиций xi и определяется при использовании алгоритма округления «до ближайшего» половиной значения младшего разряда машинного представления позиционной характеристики. Если под представление 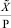 отведено k двоичных разрядов (и столько же для каждого модуля СОК), из которых k – 1 разряд соответствует дробной части, то формуле (6) будут свойственны следующие оценки погрешностей:
отведено k двоичных разрядов (и столько же для каждого модуля СОК), из которых k – 1 разряд соответствует дробной части, то формуле (6) будут свойственны следующие оценки погрешностей:
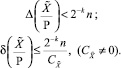 (7)
(7)
Сопоставив формулы (5) и (7), получим, что формула (6) позволяет уменьшить погрешности при вычислении приближенной позиционной характеристики в 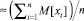 раз, где M[xi] – математическое ожидание значения i-й цифры xi в представлении модулярного числа.
раз, где M[xi] – математическое ожидание значения i-й цифры xi в представлении модулярного числа.
Пример. Возьмем исходные данные из рассмотренного ранее примера: p1 = 7, p2 = 9, p3 = 11, p4 = 13, P = 9009. Для представленных модулей СОК значения мультипликативных инверсий 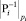 определятся следующим образом:
определятся следующим образом:
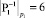 ,
, 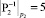 ,
,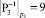 ,
, 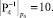
Пусть, как и ранее, требуется сравнить модулярные числа 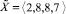 и
и 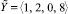 . Вычисляя их приближенные позиционные характеристики в соответствии с формулой (6), с округлением до двух десятичных разрядов после точки, получим:
. Вычисляя их приближенные позиционные характеристики в соответствии с формулой (6), с округлением до двух десятичных разрядов после точки, получим:

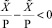 , поэтому будет сделан верный вывод, что
, поэтому будет сделан верный вывод, что 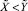 . Таким образом, при равных условиях вычисление приближенных позиционных характеристик по уточненной формуле позволило получить правильный результат сравнения чисел в СОК. □
. Таким образом, при равных условиях вычисление приближенных позиционных характеристик по уточненной формуле позволило получить правильный результат сравнения чисел в СОК. □
Заключение
Предложен способ вычисления приближенной позиционной характеристики модулярного числа, позволяющий уменьшить значения ошибок округления, по сравнению с известным способом, в 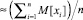 раз, где n – количество модулей СОК, а M[xi] – математическое ожидание значения i-й цифры в представлении модулярного числа. Определение приближенной характеристики по уточненной формуле требует выполнения n обращений к памяти за выборкой значений мультипликативных инверсий, n умножений, n делений и одну операцию n-операндного суммирования с отбрасыванием целой части. Таким образом, его временная сложность, выраженная в условных тактах, составляет 4n, где n – количество модулей СОК, в то время как известная формула (3) требует приблизительно 3n тактов. Очевидно, что порядок сложности при этом остается прежним, O(n). Применяя параллельные вычисления, определение приближенной позиционной характеристики по формуле (6) может быть выполнено за
раз, где n – количество модулей СОК, а M[xi] – математическое ожидание значения i-й цифры в представлении модулярного числа. Определение приближенной характеристики по уточненной формуле требует выполнения n обращений к памяти за выборкой значений мультипликативных инверсий, n умножений, n делений и одну операцию n-операндного суммирования с отбрасыванием целой части. Таким образом, его временная сложность, выраженная в условных тактах, составляет 4n, где n – количество модулей СОК, в то время как известная формула (3) требует приблизительно 3n тактов. Очевидно, что порядок сложности при этом остается прежним, O(n). Применяя параллельные вычисления, определение приближенной позиционной характеристики по формуле (6) может быть выполнено за 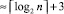 тактов.
тактов.
Рецензенты:
Шатров А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования в экономике Вятского государственного университета, г. Киров;
Частиков А.В., д.т.н., профессор, декан факультета прикладной математики и телекоммуникаций Вятского государственного университета, г. Киров.
Работа поступила в редакцию 22.02.2013.



