Одной из основных при математическом моделировании отка зов/вос ста нов лений, как последовательности случайных событий, является задача установления математического по до бия меж ду временными и вероятностными характеристиками реального процесса и его аналитической модели, причем при построении моделей процессов в сложных системах должны отражаться также структурные и логические аспекты отказов [1]. Естественной моделью для описания случайной последовательности сме ны состо яний некоторого объекта во времени является марковский, а в более об щем случае – полумарковский процесс [2, 3]. Однако наличие вза имосвязей в достаточно сложной системе приводит к необходимости учета взаимодействия элементарных полумарковских процессов и формирования единого случайного процесса, учитывающего не только смену состояний отдельных элементов моделируемой системы, но и весь комплекс взаимодействий между элементами.
Идеальным инструментарием для анализа взаимодействия процессов являются сети Петри [4, 5], однако, являясь асинхронными по опре де ле нию, модели указанного типа позволяют лишь ответить на вопросы о прин ци пи альной достижимости состояний системы, соответствующих заданным тре бо ваниям. Спрогнозировать моменты переключения в указанные состояния с помощью сетей Петри, в их классической интерпретации, затруднительно. Кроме того, ограничения в моделировании параллельных процессов с помощью сетей Петри заключаются в ограниченности логических условий продолжения процессов элементарной конъюнкцией, что не учитывает всего многообразия взаимодействий элементов в реальных сложных системах.
Объединение двух подходов к моделированию отказов в сложных системах порождает сеть Петри-Маркова (СПМ), которая представляет собой структурно-пара мет рическую модель, заданную множеством:
Y = {П, М}, (1)
где П – описание структуры двудольного графа, пред став ля ющего со бой сеть Петри; М – описание пара мет ров, на кла дываемые на структуру П, и опре деля ющих временные, вероятностные и ло гические характеристики СПМ.
Структура СПМ характеризуется множеством:
П = {A, Z, IA(Z), OA(Z)}, (2)
где A = {a1(a), ..., aj(a), ..., aJ(a)} – конечное множество позиций (в [4] вместо термина «позиция» употребляется термин «место»); Z = {z1(z), ..., zj(z), ..., zJ(z)} – конечное множество переходов; IA(Z) = {IA(z1(z)), ..., IA(zj(z)), ...,IA(zJ(z))} и OA(Z) = {IA(z1(z)), ..., IA(zj(z)), ..., IA(zJ(z))} – соответственно вход ная и выходная функции переходов; J(a) – общее количество позиций; J(z) – общее количество переходов.
В контексте задачи моделирования процесса отказов/вос становлений:
позиции мно жества A = {(a1(a), ..., aj(a), ..., aJ(a)} являются математическим подобием состояний элементов системы;
переходы множества Z = {z1(z), ..., zj(z), ..., zJ(z)} моделируют взаимодействие элементов при переключениях системы из одного состояния в другое, при этом во временной области взаимодействие может рассматриваться как «соревнование» отказов/вос ста новлений, исходом которого является переключение системы в од но из возможных сопряженных состояний;
входная функция перехода IА(zj(z)) = {а1[I, j(z)], ..., aj[I, j(z)], ..., aJ[I, j(z)]} Ì A мо де лирует мно жес т во состояний, участвующих в «соревновании», (J[I, j(z)] – общее количество позиций, составляющих входную функциюIА(zj(z)) перехода j(z));
выходная функция перехода ОА(zj(z)) = {а1[О, j(z)], ..., aj[О, j(z)], ..., aJ[О, j(z)]} Ì A мо де лирует мно жес т во исходов «соревнований» отказов/вос ста новлений элементов (J[О, j(z)] – общее количество позиций, составляющих входную функцию ОА(zj(z)) перехода j(z)).
Параметрические аспекты М сети Петри-Маркова описываются следующим множеством:
M = {q, p, f(t), L}, (3)
где q = [q1(z), ..., qj(z), ..., qJ(z)] – вектор, определяющий вероятность начала процесса в одном из переходов множества Z; p = [pj(a)j(z)] – матрица с количеством элементов J(a) ´ J(z), определяющая априорные веро ятности участия j(а)-го эле мента в одном из возможных «соревнований» zj(z); f(t) = [fj(a)j(z)(t)] – матрица с количеством элементов J(a) ´ J(z), опре деля ю щая плот нос ти рас пределения времени t пребывания процесса в состоянииaj(a) при участии в «соревновании» zj(z); L = [li(z)i(a)] – матрица с количеством элементов J(z) ´ J(a), опре де ля ющих логические условия окончания взаимодействий, с последующим переключением в состояния множестваОА(zj(z)); li(z)i(a) – элементы матрицы логических условий, равные
lj(z)j(a) = 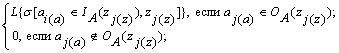 (4)
(4)
L{...} – некоторая логическая функция; s[ai(a) Î IA(zi(a)), zi(z)] – полушаг, под которым понимается логическая переменная, принимающая значения
 (5)
(5)
Таким образом, полушаги в СПМ являются функциональным подобием потока событий отказов/восстановлений в системах исследуемого класса. Полушагом si(a),j(z) = s[ai(a) Î IA(zi(a)), zi(z)] или si(z),j(a) = s[zi(z),aj(a) Î OA(zi(a)),] называется переключение состояния СПМ, при котором из позиции ai(a) Î IA(zj(z)) попадают переход zj(z), или из перехода zj(z) попадают в позицию aj(a) Î ОА(zj(z)). Два последовательных полушага образуют шаг.
Переходы zj(z) СПМ разделяются на примитивные и непримитивные. При ми тивным называется переход zj(z), для входной и выходной функций которого выполняются условия:
|IA(zj(z))| = |OA(zj(z))| = 1, (6)
где |...| – мощность соответствующего множества.
Если zj(z) – примитивный переход и аi(а) Î IA(zj(z)), аj(а) Î OA(zj(z)), то l j(z) j(а) = [аi(а), zj(z)].
Все остальные типы переходов являются непримитивными. Непри ми тив ные переходы (НП) образуют подмножество Zzn = {z1(zn), ..., zj(zn), ..., zJ(zn)} Ì Z, которое, в свою очередь, может быть разделено на подмножества поглощающих, синхронизирующих и стартовых переходов.
Поглощающим, или конечным называется НП ZE = {z1(E), ..., zj(E), ..., zJ(E)} Ì Zzn, для выходной функции которого выполняется условие
OA(zj(Е)) = Æ, (7)
где Æ = {} – пустое множество.
Для поглощающего перехода zj(z) для всех j(а) l j(z) j(а) = 0.
Стартовым или синхронизирующим может быть любой НП zj(zn), для которого выполняется условие zj(zn) Ë ZE.
Если стартовый переход zj(z) не является одновременно синхронизирующим, то IA(zj(z)) = Æ и l j(z) j(а) = 1 для всех аj(а) Î OA(zj(z)).
Подсетью
Пj(п) = {Aj(п), Zj(п), IA(Zj(п)), OA(Zj(п))} (8)
СПМ (2) называется сеть, для которой Aj(п) = {a1[a,j(n)], ..., aj[a,j(n)], ..., aJ[a,j(n)]} Í A, Zj(п) = {z1[z,j(n)], ..., zj[z,j(n)], ..., zJ[z,j(n)]} Í Z, IA(Zj(п)) Í IA(Z), OA(Zj(п)) Í OA(Z).
Подсеть (8) также является двудольным ориентированным графом. Заменим дуги (aj[a,j(n)], zj[z,j(n)]) и (zj[z,j(n)], aj[a,j(n)]), aj[a,j(n)] Î Aj(п), zj[z,j(n)] Î Zj(п), 1[a, j(n)] £ j[a, j(n)] £ J[a, j(n)], 1[z, j(n)] £ j[z, j(n)] £ J[z, j(n)] двудольного графа (8) на ребра {aj[a,j(n)], zj[z,j(n)]} и {zj[z,j(n)], aj[a,j(n)]}.
Тогда подсеть (8) будет называется связной подсетью, если между двумя про из вольными различными вершинами множества Aj(п) È Zj(п), независимо от их типа (позиция или переход), существует хотя бы один путь.
Пусть структура подсети (8) тако ва, что в ней кроме примитивных существует также подмножества переходов Zj(п),В = {z1[z,j(n),В], ..., zj[z,j(n),В], ..., zJ[z,j(n),В]} Ì Zj(п) и Zj(п),Е = {z1[z,j(n),Е], …, zj[z,j(n),Е], ..., zJ[z,j(n),Е]} ÌZj(п),
для которых
IA(zj[z,j(n),В]) Ç Aj(п) = Æ, |OA(zj[z,j(n),В]) Ç Aj(п)| = 1; (9)
ОA(zj[z,j(n),Е]) Ç Aj(п) = Æ, m[IA(zj[z,j(n),E]) Ç Aj(п)] = 1. (10)
Связная подсеть (8), у которой множество переходов Zj(п) разбивается на непересекающиеся подмножества, для которых справедливы свойства (6), (9) или (10) называется элементарной подсетью Петри-Маркова (ЭППМ). Функциональным подобием переключений внутри ЭППМ является процесс отказов и восста нов лений единственного элемента системы, рассматриваемого без взаимо дей ствия с другими элементами. Переходыzj[z,j(n),В] Î Zj(п),В являются стар то выми переходами ЭППМ Пj(п), они моделируют начало эксплуатации элемента. Переходы zj[z,j(n),Е] Î Zj(п),Е являются конечными пе реходами ЭППМ Пj(п), они моделируют отказные ситуации. Остальные переходы являются примитивными и моделируют переход элемента от состояния функционирования в составе системы более высокого уровня в состояние восстановления после отказа, или из состояния восстановления в состояние функционирования.
Для всех ЭППМ, моделирующих процесс отказов/восстановлений, в дополнение к условиям связности, можно потребовать выполнения условия достижимости хотя бы одного перехода подмножества Zj(п),Е из любого перехода подмножества Zj(п),B
В общем случае структура СПМ П может быть пред став лена в виде объединения ЭППМ Пi(n)
![]() . (11)
. (11)
Объединение пересечений ЭППМ является подмножеством синхронизирующих переходов множества непримитивных переходов всей сети Zzn:
Zzn = ![]() Ê
Ê ![]() =
=![]() . (12)
. (12)
Полное множество непримитивных переходов формируется в результате объединения подмножества ![]() с под мно жеством ZE и тех из начальных, или стартовых переходов ZB, для которых выполняется условие IA(ZB) = Æ, т.е.
с под мно жеством ZE и тех из начальных, или стартовых переходов ZB, для которых выполняется условие IA(ZB) = Æ, т.е.
Zzn = ZE È ZB È![]() .
.
Общее количество ЭППМ, J(п), равно количес т ву элементов, формирующих отказоустойчивую систему на данном уровне иерархии.
Следует особо отметить, что структура СПМ, моделирующей отказоустойчивую систему, мало походит на структуру моделируемого объекта. Поэтому при исследовании отказоустойчивости сложных систем рекомендуется при формировании модели отказов/восстановлений учитывать влияние отказов элементов на их возможные по сле д ст вия для системы в целом. Причинно-следственный анализ отказов отдельных эле мен товслабо формализуется и традиционно является частью деятельности экспертов в конкретной пред метной области. Для проведения подобного анализа необходимо иметь полный комплект конструкторской документации и детальное описание нормального процесса функциониро вания элементов и системы в целом. Указанные документы дают исходный материал для построения структурно-пара мет ри ческой модели процесса отказов/восстановлений в системе.
Поясним подход к моделированию на примере. Пусть система состоит из двух физических элементов e1 и e2, в результате функционирования которых они могут перейти в состояния возникновения перемежающегося отказа (сбоя), состояния отказа, допускающего восстановление, состояние отказа, не допускающего восстановление. В результате ремонта элементу может быть нанесен непоправимый ущерб, или он может быть переведен в работоспособное состояние. Система становится неработоспособной в случае неработоспособности обо их элементов. Структура системы и СПМ, ее моделирующей приведены на рис. 1.
На рис. 1 а: 1 и 2 – элементы системы, s1, s2, s3, s4 – переключатели, позволяющие производить отключение элемента на время проведения ремонтных работ. На рис. 1 б: П1 и П2 – соответственно, ЭППМ, моделирующие процессы в первом и втором элементах; а1, а3 – позиции, моделирующие процесс функционирования первого и второго элементов, соответственно; а2, а4 - позиции, моделирующие процесс восстановления первого и второго элементов, соответственно; z1 – стартовый переход; z2, z5 – переходы, моделирующие возникновение перемежающегося отказа (сбоя), в первом и втором элементах, соответственно; z3, z6– переходы, моделирующие возникновение отказов, поддающихся восстановлению в первом и втором элементах, соответственно; z4, z7 – переходы, моделирующие момент возврата первого и второго элементов, соответственно, в работоспособное состояние.
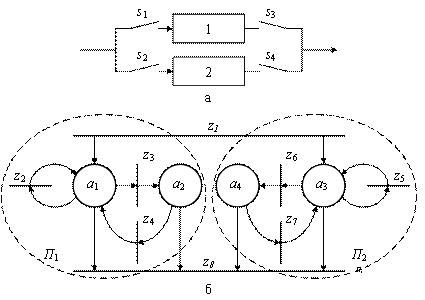
Рис. 1. Система из двух элементов (а) и СПМ, ее моделирующая (б)
Структура СПМ описывается множеством
П = {{a1, a2, a3, a4}, {z1, z2, z3, z4, z5, z6}, {{}, {a1}, {a1}, {a2}, {a3}, {a3}, {a4}, {a1, a2, a3, a4}}, {{a1, a3},{a1}, {a2}, {a1}, {a3}, {a4}, {a3}, {a1}, {}}}.
Вектор начала процесса имеет вид (процесс с вероятностью единица начинается в переходе z1)
q = (1, 0, 0, 0, 0, 0, 0, 0).
Матрицы вероятностей и плотностей распределения имеют вид:
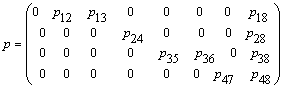 ;
;
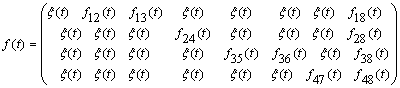 ,
,
где ![]() (срабатывание в бесконечности); d(t) – d-функция Дирака.
(срабатывание в бесконечности); d(t) – d-функция Дирака.
Матрица логических условий имеет вид:
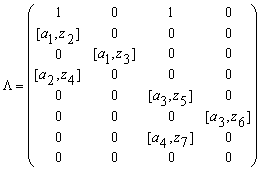 .
.
Работа выполнена при поддержке Российского фонда фундаментальных исследований
СПИСОК ЛИТЕРАТУРЫ:
1. Ушаков И.А. Вероятностные модели надежности информационно-вы числительных систем. – М.: Радио и связь, 1991. – 132 с.
2. Ярлыков М.С., Миронов М.А. Марковская теория оценивания слу чай ных процессов. – М.: Радио и связь, 1993. – 460 с.
3. Сильвестров Д.С. Полумарковские процессы с дискретным мно же ст вом состояний. – М.: Сов. радио, 1980. – 272 с.
4. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.
5. Лескин А.А., Мальцев А.М., Спиридонов А.М. Сети Петри в моделирова нии и управлении. – Л.: Наука, 1989. – 135 с.



