При исследовании надежности и долговечности деталей и узлов молота возникает необходимость в определении действующих нагрузок. Прочность деталей молота, качественные показатели этой машины зависят от силы сопротивления поковки деформированию. Доказано, что динамический расчет падающих частей ковочного молота без учета деформации поковки совершенно недопустим [1, 8].
Подавляющее большинство заготовок перед дальнейшей ковкой проходит операцию осадки, при которой в результате продольного удара увеличивается площадь поперечного сечения заготовки за счет уменьшения ее высоты.
Высокие уровни нагружения вызывают в заготовках ковочных молотов значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации, которые и составляют осадку. Т.е. в заготовках имеют место вязкоупругие деформации.
Таким образом, падающие части ковочного молота в процессе ударного взаимодействия с заготовкой можно моделировать сложной вязкоупругой стержневой системой с распределенными параметрами, соударяющейся с препятствием. В качестве математической модели предполагается принять разогретую заготовку в виде вязкоупругого тела Максвелла.
Для решения поставленной задачи используем модификацию метода конечных элементов (МКЭ), основанную на точном интегрировании дифференциального уравнения для конечного элемента [3], позволяющую рассчитывать продольные и поперечные колебания стержней ступенчато-переменного сечения с учетом или без учета рассеяния энергии при соударении с жестким препятствием [4, 9]. Данный подход был реализован в работе [5] для исследования напряжений и деформаций, возникающих в рабочих частях ковочного молота при ударе о заготовку, где было получено хорошее экспериментальное подтверждение предварительных теоретических расчетов.
В данной работе делается попытка оценки деформаций, возникающих в заготовке при ударе о нее падающих частей ковочного молота.
Учет рассеяния энергии является важной частью данных исследований. Это достигается учетом демпфирования, путем замены всех жесткостных характеристик комплексными величинами, описывающими одновременно жесткость конструкции и явления затухания колебаний.
Для учета упругого рассеяния энергии согласно Сорокину С.Е. [6] для частотно-независимого трения все характеристики упругости системы заменять комплексными величинами, в данном случае:
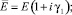
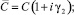
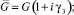
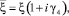
где γ – коэффициент сопротивления.
Для заготовки, обладающей одновременно упругостью, вязкостью и пластичностью в различных формах и соотношениях и моделируемой элементом Максвелла, учет рассеяния энергии будем осуществлять согласно [7].
Для вязко-упругого элемента Максвелла существуют следующие зависимости:
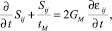
где tМ – время релаксации напряжений; Sij – тензор напряжений; εij – тензор деформаций.
Вводя параметр преобразования Лапласа 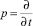 и учитывая, что при построении АФЧХ p = iω, получим:
и учитывая, что при построении АФЧХ p = iω, получим:
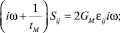
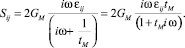
Откуда получаем выражения для характеристики E:
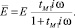
Коэффициент tМ определяется экспериментальным путем.
Из системы разрешающих уравнений находятся изображения перемещений в узлах системы. Для получения переходного процесса используется дискретное преобразование Фурье. Результат можно получить, осуществив численное интегрирование при t = 0…∞ по формуле
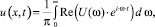
где u(x, t) – продольное перемещение поперечного сечения; х – координата сечения; t – время; ω –частота.
Предлагаемый подход справедлив для стержней неограниченной длины, поэтому разбиение на участки молота можно проводить в любых сечениях, но наиболее целесообразно там, где меняются физические или геометрические характеристики объекта.
Расчетная схема рассматриваемой задачи представлена на рис. 1.
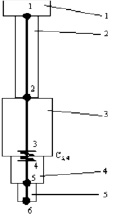
Рис. 1. Падающие части ковочного молотапри ударе о заготовку: 1 – поршень, 2 – шток, 3 – баба, 4 – верхний боек, 5 – заготовка
Таким образом, расчетная схема ковочного молота, представленная на рис. 1, будет состоять из 6 узлов, на участках которых имеют место продольные колебания. Участок 3–4 моделирует стык. На завершающей стадии удара верхний боек считается присоединившимся к заготовке, что подтверждается экспериментально.
Расчетной схеме (рис. 1) соответствует следующая система разрешающих уравнений:
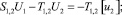
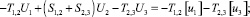
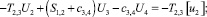
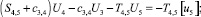
где 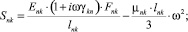
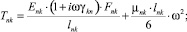
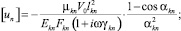
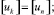
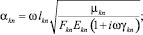
n, k – индексы, указывающие соответственно начало и конец участка; j – номер узла (i = 1,2…19); i – мнимая единица, 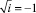 ; Еnk – модуль упругости участка nk, Па; Fnk – площадь поперечного сечения участка nk, м2; lnk – длина участка nk, м; mnk – масса единицы длины стержня участка nk, кг/м; V0 – скорость соударения с заготовкой, м/с; γnk – коэффициент сопротивления участка nk; ω – частота колебаний, с–1.
; Еnk – модуль упругости участка nk, Па; Fnk – площадь поперечного сечения участка nk, м2; lnk – длина участка nk, м; mnk – масса единицы длины стержня участка nk, кг/м; V0 – скорость соударения с заготовкой, м/с; γnk – коэффициент сопротивления участка nk; ω – частота колебаний, с–1.
Решение построенной системы уравнений осуществлялось при исходных данных, представленных в табл. 1, при V = 7 м/с. Параметры падающих частей соответствуют параметрам ковочного паровоздушного молота модели М1345. В работе [2] показано, что модуль упругости стали, нагретой до температуры 1200…1300 °С, уменьшается в 25…30 раз по сравнению с холодной сталью, а меди – уменьшается в 6…7 раз при нагреве с 15 до 800 °С, алюминия – в 30…35 раз при нагреве до 600 °С.
Таблица 1
Исходные данные для расчетов
|
Начало участка |
Конец участка |
Е, Па |
F, м2 |
ρ, кг/м3 |
|
|
1 |
2 |
1,6 |
2,1∙1011 |
0,024 |
7800 |
|
2 |
3 |
0,906 |
2,1∙1011 |
0,39 |
7800 |
|
3 |
4 |
Пружина с жесткостью 75∙106 кг/м |
|||
|
4 |
5 |
0,3 |
2,1∙1011 |
0,204 |
7800 |
|
5 |
6 |
0,115 |
7∙109 |
0,0016 |
7620 |
В результате численных расчетов, осуществленных с помощью программного комплекса MathCAD2001, получен переходный процесс в точке контакта верхнего бойка молота с заготовкой, представленный на рис. 2. Получено, что осадка заготовки после первого удара составляет 21 мм. Что согласуется с экспериментальными данными.
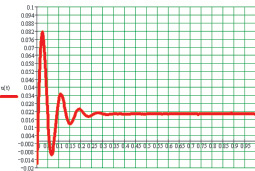
Рис. 2. График перемещений 5 узла системы
Для проверки адекватности построенной математической модели в основном производстве ЗАО «Авиастар-СП» на операциях свободной ковки были проведены испытания с целью исследования осадки заготовки в процессе ударного взаимодействия с падающими частями ковочного молота при фиксированном ходе бабы. Испытания проводились в условиях выполнения производственной программы при ковке заготовок в количестве 5 шт. Для контроля размеров заготовки до и после удара падающих частей молота использовали кронциркуль.
Условия испытаний:
1. Молот ковочный паровоздушный арочного типа с массой падающих частей 3150 кг. Модель М1345. Заводской номер № 107.
2. Режим ковки – режим единичного удара.
3. Результаты опытно-промышленных испытаний представлены в табл. 2.
Таблица 2
Результаты экспериментальных исследований
|
Материал заготовки |
Температура ковки, °С |
Форма и размеры заготовки |
Ход бабы, мм |
Размеры заготовки после 1 удара |
|
|
1 |
30ХГСА |
1170 |
∅ 45×115 |
635 |
∅ 50×93 |
|
2 |
30 ХГСА |
1170 |
∅ 45×80 |
670 |
∅ 50×65 |
|
3 |
12Х18Н10Т |
1170 |
∅ 210×92 |
448 |
∅ 220×83 |
|
4 |
АК6 |
450 |
110×140×86 |
610 |
95×96×145 |
|
5 |
АК6 |
465 |
∅ 110×240 |
510 |
∅ 50×93 |
По результатам экспериментальных исследований составлен и подписан акт опытно-промышленных испытаний с представителями ОАО «Авиастар-СП» и УлГТУ.
Получили, что для заготовки, выполненной из стали 30ХГСА, при температуре ковки 1170 °С, ∅45×115, осадка составляет 22 мм, что хорошо согласуется с теоретическим расчетом. Расхождение составляет 4,5 %.
Вывод
– Построена математическая модель заготовки ковочного молота в виде тела Максвелла;
– выполнена проверка адекватности построенной математической модели путем сравнения теоретических расчетов с экспериментальными данными;
– получено хорошее совпадение теоретических и экспериментальных результатов. Погрешность расчетов составила 5 %.
Предлагаемый подход теоретического расчета осадки заготовки имеет ценность, заключающуюся в возможности предварительной оценки ее прочности в зависимости от разных технологических режимов ковки.
Из производственной практики известны нередкие случаи образования трещин на заготовках ковочных молотов, осколков, причиняющих вред жизни и здоровью рабочих и приводящие к материальным потерям на производстве.
Возможность теоретического расчета напряжений и деформаций, возникающих в деталях ковочного молота и заготовки, позволяет назначать оптимальные технологические режимы ковки.
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск;
Дмитриенко Г.В., д.т.н., профессор Ульяновского высшего авиационного училища (института), г. Ульяновск.
Работа поступила в редакцию 07.11.2012.



