С появлением персональных компьютеров и стремительным ростом как компьютерной, так и программной индустрии в последние десятилетия все чаще и чаще человек начинает использовать новые методики в различных сферах жизни. Так, с появлением статистических пакетов, таких как Statistica, Spss, Stadia, появилась возможность оперативного решения статистических задач в медицине, экономике, зоологии, нефтегазовой отрасли и др. за считанные минуты.
В данной статье речь пойдет о двух статистических методах: многомерном методе шкалирования и кластеризации. В реальности эти методики в основном используются раздельно независимо друг от друга. В данной работе предлагается их использование совместно, так как именно это позволит получить больший эффект от реализации этих методов в исследовании.
Для начала дадим определения этим методам. Кластеризация – это классификация объектов на основе их сходства друг с другом, когда принадлежность обучающих объектов каким-либо классам не задаётся. Многомерное шкалирование – это математический инструмент, который позволяет изобразить сходства и различия объектов в пространственной карте. И тот, и другой метод объединяет графическое представление полученного решения. В этом и состоит привлекательность этих методов. А что будет, если их совместить? Для ответа на этот вопрос потребуется разобрать эти методы более детально.
Кластерный анализ
Алгоритмы кластеризации очень похожи на алгоритмы классификации, но есть и принципиальные различия. Так, например, алгоритмы классификации позволяют отнести в определенный класс каждый объект с заранее известными параметрами, полученными на этапе обучения. В кластеризации разбиваются множества объектов на кластеры, параметры которых заранее неизвестны. В классификации количество классов строго ограничено, а в кластеризации число кластеров может быть как произвольным, так и фиксированным. Таким образом, отличием кластерного анализа от других методов классификации является отсутствие обучающей выборки (классификация без обучения), а его достоинством – возможность производить разбиение объектов не по одному параметру, а по ряду признаков.
Выделяют две группы методов кластерного анализа: иерархические и неиерархические. Различие состоит в выдаваемых на выходе данных. Иерархические алгоритмы (рис. 1) на выходе выдают некую иерархию кластеров, и мы вольны, выбрать любой уровень этой иерархии для того, чтобы интерпретировать результаты алгоритма. Неиерархические – это, фактически, все алгоритмы, которые на выходе иерархию не выдают (или выбор интерпретации происходит не по уровню иерархии).
В свою очередь иерархические методы подразделяются на агломеративные и итеративные дивизимные процедуры.
Агломеративные процедуры начинают свое выполнение с того, что каждый объект заносят в свой собственный кластер и по мере выполнения объединяют кластеры до тех пор, пока в конце не получается один кластер, включающий в себя все объекты набора.
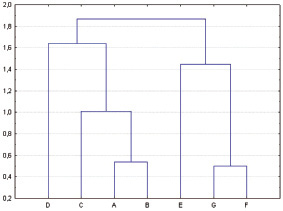
Рис. 1. Иерархическая кластеризация
Итеративные дивизимные процедуры, напротив, сначала относят все объекты в один кластер и затем разделяют этот кластер до тех пор, пока каждый объект не окажется в своем собственном кластере, исходя из задаваемых условий разбиения, которые могут быть изменены пользователем для достижения желаемого качества.
Основными методами иерархического кластерного анализа являются метод ближнего соседа, метод полной связи, метод средней связи и метод Варда.
Неиерархических методов больше, хотя работают они на одних и тех же принципах. По сути, они представляют собой итеративные методы дробления исходной совокупности. В процессе деления формируются новые кластеры, и так до тех пор, пока не будет выполнено правило остановки. Между собой методы различаются выбором начальной точки, правилом формирования новых кластеров и правилом остановки. Чаще всего используется алгоритм К-средних. Он подразумевает, что аналитик заранее фиксирует количество кластеров в результирующем разбиении.
Методы многомерного шкалирования
Для получения качественного результата многомерного шкалирования необходима информация обо всех или почти всех сходствах между различными комбинациями пар объектов и вычислительная техника. На выходе получается изображение точек, на графике близко расположенных относительно друг друга, если объекты похожи и соответственно далеко друг от друга в случае значительных различий между ними. Таким образом, входная информация для задачи многомерного шкалирования – сведения о попарных сходствах или связях анализируемых объектов (индивидуумов, семей, предприятий, отраслей и т.п.), а выходная – приписанные каждому из объектов числовые значения координат в некоторой вспомогательной (найденной в процессе решения) координатной системе.
Многомерное шкалирование по сути является альтернативой факторному и компонентному анализу. В многомерном шкалировании, так же как и в компонентном анализе, основными данными являются меры близости. При условии, что исходные данные были стандартизированы, корреляции являются значениями сходства, и расстояния вычислены с помощью евклидовой метрики по формуле (1), как метод многомерного шкалирования, так и компонентный анализ в результате воспроизведут идентичный график согласно исследованию Chatfield и Collins [3].
Как в кластер-анализе, так и в многомерном шкалировании используются меры близости. Существует большое количество мер близостей (более 25 разновидностей), и выбор той или иной из них обуславливается содержательными соображениями и спецификой имеющихся данных.
Одной из популярных мер близостей является Евклидово расстояние:
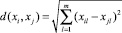 . (1)
. (1)
Другой мерой близости может быть манхэттенское расстояние, или «расстояние городских кварталов» (city-block), которое является просто средним разностей по координатам. В большинстве случаев данная мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида, однако для нее влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Манхеттенское расстояние определяется следующим образом:
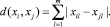 (2)
(2)
Можно определить и другие метрики, но большинство из них являются частными формами специального класса метрических функций расстояния, известных как метрики Минковского, которые можно найти по формуле:
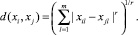 (3)
(3)
Пошаговая технология
Теперь для примера совместим результат, полученный на рис. 1, с многомерным методом шкалирования и представим на рис. 2.
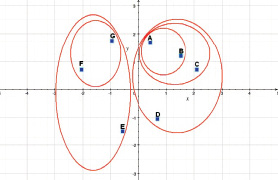
Рис. 2. Многомерное шкалирование и кластер-анализ
Представим, что точки A, B, C, D, E, F и G – это предприятия. Ось x интерпретирована как выручка, а ось y ‒ как прибыль. Овалами точки объединены в кластеры. В результате можно сделать вывод о том, что данные поделены на два кластера: первый – это предприятия с большим объемом выручки (A, B, C и D), второй – с меньшим. В дальнейшем кластеры разбиваются на другие кластеры, которые также можно охарактеризовать следующим образом (таблица). Таким образом, с помощью многомерного шкалирования и кластеризации мы расположили в двумерном пространстве компании, разбили их на группы и описали.
Разбиение по кластерам предприятий
|
A, B, C |
D |
E |
F, G |
|
Большой объем выручки |
Малый объем выручки |
||
|
прибыльный |
убыточный |
убыточный |
прибыльный |
Полученные с помощью многомерного шкалирования двухмерные проекции точек иногда вводят в заблуждение, так как две точки могут фактически находиться на большем расстоянии друг от друга, чем это отражено с помощью проекций, где они будут располагаться вблизи друг от друга. Именно по этой причине рекомендуется использовать в качестве дополнения этой модели иерархический кластерный анализ. Фактически предлагается наложить результаты, полученные с помощью иерархического кластерного анализа (рис. 1) на карту, полученную с помощью методов многомерного шкалирования. Результат наложения представлен на рисунке и на нем видно, что в большинстве случаев с помощью кластерного анализа выделялись объекты, расположенные рядом и реально соответствующие действительности.
Сравнительный анализ
Одно из главных преимуществ использования методов многомерного шкалирования и кластеризации связано с тем, что они имеют довольно существенное сходство. Так, данные о близости можно исследовать как с помощью кластерного анализа, так и многомерного шкалирования. В иерархическом кластер-анализе, так же как и в многомерном шкалировании, решение можно представить в виде координатных осей. Однако есть и большие различия. Во-первых, в кластерном анализе связь между данными о близости не может быть, как в многомерном шкалировании, представлена функциями. Во-вторых, расстояния в кластер-анализе – это не расстояния в пространстве, как в многомерном шкалировании. В-третьих, в многомерном шкалировании оценки координат являются непрерывными переменными, а в кластер-анализе ‒ дискретными.
Заключение
Поскольку кластеризация и многомерное шкалирование используют разные представления структур, они рассматриваются как дополняющие друг друга методы, проясняющие разные параметры объектов. Таким образом, предлагаемая технология заключается в реализации этапа применения методов многомерного шкалирования, а затем кластерного анализа. Реализация данной технологии позволяет классифицировать большое количество объектов при условии наличия информации о них. Так, применение данной технологии в банковской сфере позволит разделить и классифицировать по финансовым показателям или другой полученной информации компании на финансово благополучные или банкротные, расположив их на двумерной карте. В результате у кредитной организации появится возможность перед принятием решения о кредитовании узнать возможности потенциального заемщика. Данная технология также может использоваться в медицине, где объектами выступают пациенты, в политике – политические партии и движения, а также в других сферах человеческой деятельности.
Рецензенты:
Видовский Л.А., д.т.н., профессор, заведующий кафедрой ВТ и АСУ КубГТУ, г. Краснодар;
Ключко В.И., д.т.н., профессор кафедры ВТ и АСУ КубГТУ, г. Краснодар.
Работа поступила в редакцию 07.11.2012.



