В работе [1] сформулирована бимолекулярная модель разветвленной цепной реакций импульсного инициирования АТМ и проведен ее кинетический анализ. Схема стадий модели имеет вид:
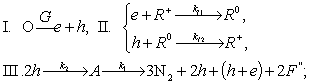(1)
где 
- центры рекомбинации в различных зарядовых состояний, 2
- комплекс, состоящий из двух анионных вакансий с размещенными там тремя молекулами азота.I - генерация e.h. пар внешним излучением. II - рекомбинация e.h. пар на объемных и поверхностных локальных центрах, при этом скорость рекомбинации носителей лимитируется захватом дырки на нейтральном центре: 
. III - взаимодействие двух дырок, локализованных в соседних узлах кристаллической решетки, с образованием промежуточного комплекса А (молекула N6 находящаяся внутри анионной бивакансии), последующим его распадом на молекулярный азот (N2) и образование 2F´ - центра с выделением энергии, идущей на генерацию носителей, является стадией развития цепи. C учетом уравнений баланса, динамика процесса инициирования будет полностью описываться системой:
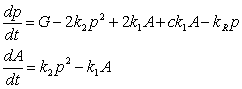(2)
где G = α·H0/E·τu - скорость генерации e.h. пар импульсным излучением, Е - энергия образования e.h. пары, α - показатель поглощения образцом излучения.
В экспериментальных работах скорость взрывного разложения азида серебра характеризуют экспоненциальной константой нарастания сигнала, получаемой при аппроксимации его экспоненциальной функцией. В рамках модели цепной реакции также наблюдается экспоненциальный рост концентраций носителей цепи. Предположим, что рост сигнала свечения вызван ростом концентрации носителей цепи в образце.
Для получения наблюдаемой константы скорости экспоненциального роста концентрации носителей цепи получим значение мгновенной константы скорости экспоненциального роста. Линеаризуем систему кинетических уравнений вблизи концентрации дырок равной р0. Собственное число системы уравнений, отвечающее за рост концентраций носителей цепи будет следующим:
(5)
Полученную константу роста концентрации носителей цепи можно назвать «мгновенной». Выражение для kм можно без большой потери точности заменить приближенной формулой:
(5)
Наблюдаемую константу экспоненциального роста концентрации носителей цепи получим, усреднив ее мгновенное значение по концентрации дырок. Нижняя граница определяется концентрацией после индукционного периода ~ kR/k2 ~ 1018 см-3 [1]. Экспериментальная константа роста сигнала определяется до его полувысоты, по этому за верхнюю границу усреднения следует принять половину максимальной концентрации дырок, значение которой ~ (1÷10)·1019 см-3. Тогда получаем:
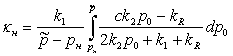(6)
Интегрируя, и подставляя границы усреднения, получаем:
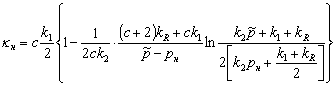(7)
Уменьшение скорости цепной реакции при уменьшении диаметра зоны облучения можно объяснить генерацией e.h. за счет энергии химической реакции не только в облученной зоне, но и в некотором слое толщиной r0 вне еe. Тогда чем меньше диаметр зоны облучения, тем большее количество носителей цепи образовано вне нее. Соответственно, образовавшиеся при ветвлении носители цепи будут поглощены в большем объеме, чем объем зоны облучения, что приводит к увеличению пороговой плотности энергии инициирования [2].
В условиях инициирования неодимовым лазером, энергия излучения поглощается однородно по глубине образца. Объемы, в которых были сгенерированы и поглощены носители цепи, будут относится как [(d+2r0)/d]2, где d - диаметр зоны облучения. В работе [2] было экспериментально показано, что в акте ветвления 2 дырки образуются в точке ветвления и еще одна электрон-дырочная пара в r0 окрестности этой точки.
Из (7) следует, что kн ~ с. Согласно [2]:
(8)
Тогда получаем зависимость средней константы роста концентрации носителей цепи от диаметра зоны облучения:
(9)
где константа k∞ - значение константы роста сигнала при бесконечно широком пучке.
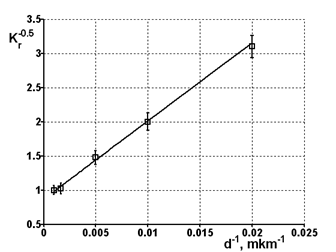
Рис. 1. Зависимость эффективной константы скорости экспоненциального роста сигнала взрывного свечения 
от диаметра зоны облучения. Точки - эксперимент, линия - аппроксимация по формуле (9).
На рис. 1 приведено сравнение теоретической и экспериментальной зависимостей. Видно, что в координатах модели (9) экспериментальные данные подчиняются линейной зависимости. Значение параметра модели r0 составило 60 ± 5 мкм, что неплохо согласуется со значением, определенному из зависимости плотности пороговой энергии инициирования от диаметра лазерного пучка [2].
Работа поддержана грантом РФФИ (№ 07-03-01099).
СПИСОК ЛИТЕРАТУРЫ:
- Кригер В.Г., Каленский А.В. Инициирование азидов тяжелых металлов импульсным излучением. // Хим. Физика. - 1995. - № 4. - C. 152-160.
- Каленский А.В., Кригер В.Г., Звеков А.А., Боровикова А.П. Новый механизм передачи энергии твердофазной цепной в азиде серебра. // Фундаментальные проблемы современного материаловедения. Т. 4. № 3. 2007. С. 66-72.