Постановка задачи. Рассматривается задача прогнозирования геолого-геофизических параметров для неоднородных сред на основе рассеянных экспериментальных данных как задача нечеткого логического вывода. Такая задача возникает, например, при прогнозирование подсчетных параметров и оценке запасов месторождений углеводородного сырья по промыслово-геофизическим данным. Отличительной чертой рассмотрений служит моделирование функций принадлежности нечетких величин и нечетких отношений решениями уравнения диффузии и интерпретация рассеяния данных как проявления неоднородности изучаемого объекта.
Измеряемые в скважинах для изучаемого продуктивного пласта данные s = {si, i = 1...I} в силу его неоднородности характеризуются облаком своих значений для каждого si. Для каждого месторождения и типа коллектора имеются полученные лабораторно-аналитическим путем данные о связи между параметрами si и характеристиками коллекторов, таких как пористость, в некоторых случаях проницаемость, глинистость, характеристики флюидонасыщения и так далее. Эту группу параметров обозначим q = {qj, q = 1...J}, а данные (s, q), представляющие собой совокупность измерений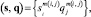 
i = 1...I, j = 1...J, m(i, j) = 1...M(i, j), где M(i, j) это число образцов, на которых проводились измерения для параметров (si, qj). Совокупность (si, qj) представляет собой облако точек в соответствующем фазовом пространстве параметров, разброс которых имеет причиной неоднородность изучаемых образцов и традиционные ошибки различного генезиса. Параметры qj – связаны с искомыми подсчетными – промысловыми параметрами f = (fl, l = 1...L), что отражено в полученных в результате экспериментов полем рассеяния точек
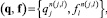n(j, l) = 1...N(j, l),
где N(j, l) ‒ число измерений для параметров (qj, fl). Например, в качестве параметра f выступает коэффициент пористости по керну, коэффициента нефте- (газо-) насыщения, проницаемости и так далее. Эти – подсчетные параметры и служат для расчета запасов углеводородного сырья, наряду с пространственно-геометрическими характеристиками залежи. Задача нахождения подсчетных параметров f и последующей оценки запасов углеводородов состоит в расчете для залежи и каждого продуктивного пласта параметров значения f по заданным измеренным s и данным рассеяния (s, q):(q, f);:
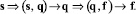(1)
Цепочка прогноза (1) в реальных условиях может быть более широкой за счет большего числа промежуточных параметров, (q, f1), (f1, f2), ..., (fK, f) и выглядит следующим образом:
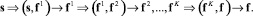(2)
Кроме того, таких цепочек может быть несколько, опирающихся на различные параметры, но приводящие к различному по значениям прогнозу одного и того же параметра:
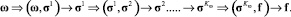(3)
Итогом прогноза по каждой из цепочек служат, вообще говоря, несовпадающие поля рассеяния, характеризующиеся функциями принадлежности для прогнозируемого параметра f, которые должны быть согласованы. В том случае, когда принимается модель данных, в которой рассеяние, присутствующее во всех компонентах цепочки (1) связано лишь с погрешностями, задача прогноза значений параметра f решается методами математической статистики, обеспечивающих исключение или существенное ослабление погрешностей в заданных предположениях о их характере. Данные заменяются их статистическими оценками, связи находятся методами регрессионного анализа [1, 2], переходы в цепочке (1) реализуются обычной подстановкой одних уравнений регрессии в другие.
Совершенно иная модель данных возникает в предположении, что рассеяние есть следствие неоднородности среды и не сводимо к влиянию ошибок измерений. В таком понимании рассеяние данных есть объективная информация о свойствах неоднородности среды, и прогнозирование параметра по цепочке (1) своим итогом имеет поле рассеяния для прогнозного параметра. Инструментом для прогноза функций рассеяния служат принципы нечеткой математики, развитой Лотфи Заде [3], и правила нечеткого вывода [4]. В основе этих методов лежит представление о функциях принадлежности, характеризующих рассеяние данных, роль которых играют фундаментальные решения уравнения диффузии. Это позволяет обеспечить изучение моделей неоднородностей среды как наблюдаемых эффектов диффузии первоначально распределенных концентраций и обеспечить конструктивный прогноз полей рассеяния параметров по цепочке (1) на основе правил нечеткого вывода.
Модельные представления поля рассеяния. Следует выделить два типа полей рассеяния.
1. Поле рассеяния данных – это их функции принадлежности для исходных, регистрируемых, промежуточных и прогнозных параметров, рассматриваемых как нечеткие величины. Для них введем обозначение: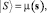 
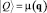и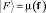 
соответственно.
2. Поле рассеяния экспериментально установленных связей (s, q) и (q, f) – это функции принадлежности для отношений между функциями принадлежности измеряемых – промежуточных и прогнозных параметров. Они обозначаются μ(ξ) = μ(s, q), ξ = (s, q); μ(ζ) = μ(q, f), ζ = (q, f). Диапазон значений (область определения μ(s, q), μ(q, f)) параметров в этих связях определен реальными экспериментальными данными A(ξ) и A(ζ) для значений параметров ξ = (ξ i,j):
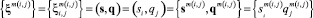
и :ζ = (ζj,l):
.
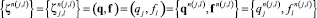Он включает в себя области определений функций μ(s) и μ(q). Индексы i, j, нумеруют компоненты многомерного параметра, а индексы m(i, j) и n(j, l) количество измерений, которое, вообще говоря, свое для каждой комбинации (i, j) и (j, l).
В фазовом пространстве Ξ, образованном параметрами ξ = (ξ i,j), каждое измеренное значение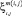 
из A(ξ) порождает функцию принадлежности μm(i, j)(ξ) во всем Ξ, как меру возможности значения параметра ξ после выполненного одиночного измерения.
Очевидно, что: 0 ≤ μ m(i, j)(ξ) ≤ 1- – условие нормировки и μm(i, j)(ξ) имеет максимум в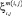 
и монотонно убывает с удалением от 
.
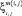Функция принадлежности для ξ = (ξ i,j), возникающая после выполнения всей совокупности измерений, определена правилом
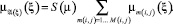(4)
Здесь S(μ) – нормировочный множитель.
Примем модель, согласно которой μm(i, j)(ξ) аппроксимируется фундаментальным решением уравнения диффузии на плоскости значения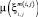 
на расстояние 
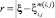, продолжавшаяся время τ. Для уравнения диффузии:
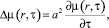(5)
где a – коэффициент диффузии, его фундаментальное решение на плоскости есть
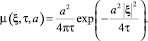(6)
Тогда
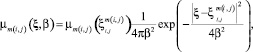
где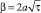 
‒ эффективный параметр глубины диффузии.
Учитывая (4) A(ξ), получим
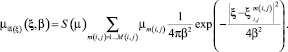(7)
Здесь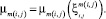 
В частности,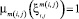 
для всех m(i, j).
Аналогичным образом строится функция принадлежности μA(ζ)(ζ, β) для эксперимента A(ζ):
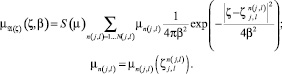(8)
Функция принадлежности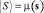 
, рассматриваемая как поле рассеяния исходных данных, по которым реализуется прогноз, конструируется по результатам измерения sk, k = 1...K аналогично тому, как это выполнено для (7) и (8):
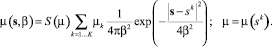(9)
Правила прогнозирования. Для реализации цепочки прогнозирования (1) воспользуемся правилом логического вывода, основанного на композиции Мамдани [4]: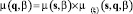 
. С учетом введенных аппроксимаций для функций принадлежности, выраженных через фундаментальные решения уравнения диффузии с эффективным параметром глубина диффузии β, получим правило расчета функций рассеяния.
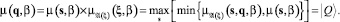(10)
Аналогично
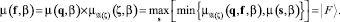(11)
Объединяя (10) и (11), получим
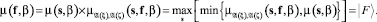(12)
Здесь
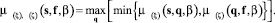(13)
Подставляя сюда выражения для функции рассеяния, получаем: решение задачи (12), реализуемое на основе (13) с использованием (8) и (9) называется прямой задачей рассеяния для прогноза параметров.
Повышение разрешенности прогнозного распределения параметров.
В расчетах, описанных выше, параметр β должен подбираться на этапе формирования функции рассеяния μ(s, β) по правилу (9) по неформализованным принципам адекватного представления неопределенности данных в разных точках области определения параметров. Однако получаемое в итоге прогнозное значение функции рассеяния μ(f, β) для параметра f может оказаться чрезмерно размытым. Для повышения контрастности заметим, что решения уравнения (5), которое обозначим в виде оператора A(τ), действующего на начальные условия μ(r, 0), образуют полугруппу относительно параметра τ и:
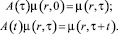
С другой стороны, в силу, определения фундаментальных решений
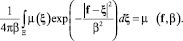(14)
Здесь Ξ – область определения параметра f.
Уравнение (14) следует рассматривать как обратную задачу относительно μ(ξ), которая называется обратной задачей рассеяния. Для нахождения μ(ξ) по найденному в результате решения прямой задачи рассеяния μA(f, β) следует воспользоваться хорошо развитыми для этого случая методами решения некорректных задач [5]. С этой целью необходимо выделить последовательность возрастающих разрешенных функций рассеяния параметра, соответствующих возрастающей последовательности эффективного параметра глубины диффузии β.
Выводы
Задача прогнозирования геолого-геофизических параметров рассматривается как задача рассеяния поля данных измерений геофизических параметров на поле рассеяния, характеризующего экспериментальные данные о связях между параметрами в соответствующем фазовом пространстве параметров.
Поля рассеяния аппроксимируются решениями уравнения диффузии и служат аппроксимацией для функции принадлежности, характеризующей нечеткие измеряемые данные и нечеткие отношения между измеряемыми и прогнозными параметрами.
Прямая задача рассеяния состоит в синтезе представлений о поле рассеяния для прогнозных параметров как следствия неоднородности среды и принципов логического вывода Мамдани, примененного к диффузионным представлениям для функций принадлежности нечетких величин и нечетких отношений.
Решение обратной задачи рассеяния направлено на получение большей локализации в получаемой функции рассеяния и состоит в подборе оптимального параметра глубины диффузии.
Разработанный метод прогнозирования поля рассеяния параметров обладает очевидными преимуществами в сравнении с традиционной техникой регрессионного анализа. Они состоят в следующем:
Открывается научно обоснованная возможность изучения свойств неоднородности распределения прогнозных параметров на основе эффекта рассеяния результатов прогноза , который ранее относился к ошибкам и отбрасывался без должного анализа;
Результат прогнозирования опирается на реально регистрируемые данные и исключает искусственно введенные представления об аналитическом виде уравнений рассеяния.
Повышается объективность прогноза за счет автоматического учета различной плотности данных в разных участках фазового пространства параметров
Рецензенты:
Бурмистрова О.Н., д.т.н., профессор, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Павлов А.И., д.т.н., профессор, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Работа поступила в редакцию 23.07.2014.
Библиографическая ссылка
Кобрунов А.И. ПРЯМЫЕ И ОБРАТНЫЕ ЗАДАЧИ РАССЕЯНИЯ ПРИ ПРОГНОЗЕ ФИЗИКО-ГЕОЛОГИЧЕСКИХ ПАРАМЕТРОВ ПО ГЕОФИЗИЧЕСКИМ ДАННЫМ // Фундаментальные исследования. – 2014. – № 9-6. – С. 1195-1199;URL: https://fundamental-research.ru/ru/article/view?id=35037 (дата обращения: 23.11.2024).