Особое внимание в России в наше время уделяется газотурбинным установкам (ГТУ), предназначенным для привода синхронных генераторов в составе мини-электростанций мощностью от 2,5 до 20 МВт и более. Этот интерес объясняется тем, что ГТУ обладают высокой надежностью, низким уровнем шума при работе, относительно небольшими размерами и неприхотливостью в дальнейшем использовании. Также в настоящий момент электростанции, работающие на газовом топливе, имеют наиболее привлекательную для потребителя удельную стоимость строительства и низкие затраты при последующей эксплуатации. Вполне понятно, что при дальнейшей эксплуатации ГТУ у технологического персонала и руководства возникает потребность в повышении КПД газотурбинной установки и улучшении показателей качества вырабатываемой электроэнергии. Одним из способов решения данной задачи может быть автоматизация настройки систем автоматического управления (САУ) ГТУ. Обычно настройку регулятора проводят на стенде и окончательно на реальном объекте, а так как это не простая задача, всегда существует риск снижения качества электроэнергии по частоте и напряжению и даже риск срыва технологического режима, что увеличивает затраты для любого предприятия. Для уменьшения риска возможно использование математической модели, которая повторяла бы поведение реальной ГТУ в составе ГТЭС. Также необходимо отметить, что для настройки регулятора необходима такая модель, которая способна с высокой скоростью моделировать переходные процессы. Алгоритм проведения настройки регулятора при использовании математической модели изображен на блок-схеме (рис. 1).
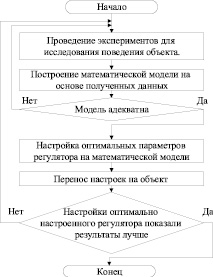
Рис. 1. Алгоритм настройки регулятора при помощи математической модели
Создание математической модели
На данный момент существует множество различных типов математических моделей ГТУ. Например, сложные поэлементные модели являются самым точным вариантом отображения поведения исследуемого объекта (ГТУ), так как они состоят из уравнений, описывающих физические процессы, происходящие на установке. Однако процесс получения данных моделей очень трудоёмкий, и они, как правило, обладают довольно низкой скоростью работы. Поэтому они, как правило, используются при проектировании ГТУ.
Модели, полученные с помощью идентификации, имеют более высокую скорость работы, но это неизменно сказывается на точности данного типа моделей.
Поэтому целесообразно исследовать альтернативный путь: получить модель, основанную на базе нейронной сети. Данный выбор обусловлен тем, что газотурбинная электростанция является нелинейной системой [1], а из источников [7] известно, что нейронные сети способны аппроксимировать любой вид нелинейности. К тому же нейронные сети, имеют высокую скорость работы и уже показывали хорошие результаты в моделировании газотурбинных установок [3, 4, 8, 9].
Настройка параметров нейронной сети
При настройке нейронной сети, во-первых, необходимо определиться с архитектурой нейронной сети. В нашем случае для построения модели был выбран многослойный персептрон, прежде всего за простоту в реализации и то, что данный тип нейронной сети уже ранее использовался для идентификации газотурбинной установки [3]. Также к данной архитектуре было решено добавить наличие обратных связей. Благодаря этому нейронная сеть показала улучшение в качестве обучения. Необходимо отметить, что у данной нейронной сети было решено использовать 2 скрытых слоя по 30 нейронов в каждом слое, а функцией активации выбран гиперболический тангенс, который описывается следующим выражением (1):
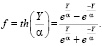 (1)
(1)
Область значений данной функции находится в интервале (0; 1), а данная функция изображена на рис. 2.
На рис. 3 предоставлена архитектура полученной нейронной сети, где nTK – скорость вращения турбокомпрессора; nCT – скорость вращения свободной турбины; U – напряжение СГ; I – ток СГ; NG – мощность СГ; IF – ток возбуждения; GT – расход топлива; UF – напряжение обмотки возбуждения; ZN – статическая нагрузка СГ; wabc – весовой коэффициент связи (a – индекс таблицы весов, b – номер нейрона в слое, откуда идет связь, с – номер нейрона в слое, куда приходит связь).
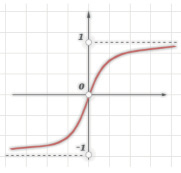
Рис. 2. Функция активации. Гиперболический тангенс
Получение модели на базе нейронной сети
Для создания модели необходимо получить данные, по которым нейронная сеть могла бы обучиться воссоздавать переходные характеристики ГТУ. Из-за отсутствия доступа к реальной установке экспериментальные данные были получены с помощью, представленной ОАО «Авиадвигатель» (г. Пермь) сложной поэлементной модели газотурбинной электростанции [3, 5].
В итоге было получено множество переходных характеристик, из которых в последующем было создано 2 выборки:
1. Обучающая выборка – данные, по которым нейронная сеть будет обучаться.
2. Тестовая выборка – независимые данные, то есть переходные процессы, которые не входили в обучающую выборку.
В обучающую выборку вошло 8 экспериментов, проведённых на сброс нагрузки при разных расходах топлива, и 5 экспериментов на наброс нагрузки. При сбросе нагрузка ГТЭС изменялась с 6000 кВт до 1000 кВт, а при набросе – с 1000 кВт до 6000 кВт. Данные были поданы на нейронную сеть, на данном этапе выбирается критерий останова, это значение ошибки, при котором нейронная сеть должна прекратить обучение. Наилучшие результаты получились при критерии останова, равном 0,3. На рис. 4 изображены изменения расхода топлива в кг/ч.
На рис. 5 и 6 изображены переходные характеристики сложной поэлементной модели и модели, основанной на базе нейронной сети, также представлена таблица, в которой приведена мера адекватности полученной модели по критерию Тейла [6].
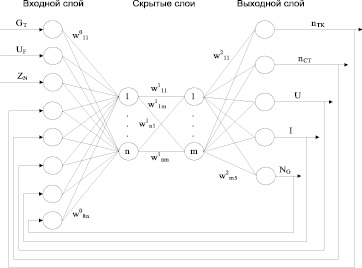
Рис. 3. Архитектура созданной нейронной сети
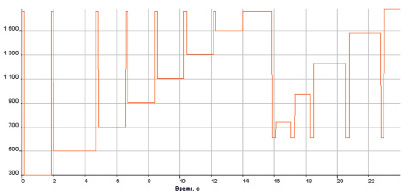
Рис. 4. Изменение расхода топлива (кг/ч) в обучающей выборке
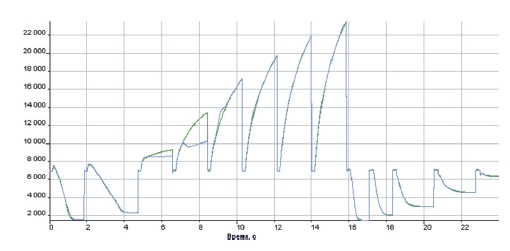
Рис. 5. Частота вращения свободной турбины (об/мин) в обучающей выборке: 1 – данные, полученные с помощью сложной поэлементной модели; 2 – данные, полученные с помощью модели на базе нейронной сети
Таблица 1
Меры адекватности модели
|
Переменная |
Мера адекватности модели |
|
Скорость вращения свободной турбины |
0,05 |
|
Действующее напряжение синхронного генератора |
0,02 |
Таблица 2
Меры адекватности модели
|
Переменная |
Мера адекватности модели |
|
Скорость вращения свободной турбины |
0,04 |
|
Действующее напряжение синхронного генератора |
0,02 |
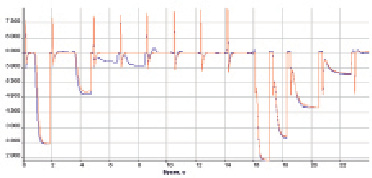
Рис. 6. Напряжение синхронного генератора (В) в обучающей выборке: 1 – данные, полученные с помощью сложной поэлементной модели; 2 – данные, полученные с помощью модели на базе нейронной сети
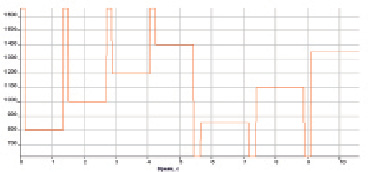
Рис. 7. Изменение расхода топлива (кг/ч) в тестовой выборке
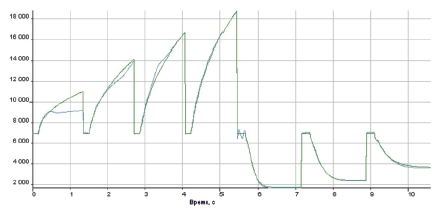
Рис. 8. Частота вращения свободной турбины (об/мин) в тестовой выборке: 1 – данные, полученные с помощью сложной поэлементной модели; 2 – данные, полученные с помощью модели на базе нейронной сети
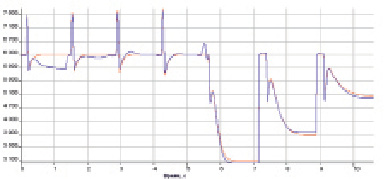
Рис. 9. Напряжение синхронного генератора (В) в тестовой выборке: 1 – данные, полученные с помощью сложной поэлементной модели; 2 – данные, полученные с помощью модели на базе нейронной сети
На следующем щаге проверяется обобщающая способность нейронной сети, а именно способна ли она моделировать переходные процессы не входившие в обучающую выборку. В тестовую выборку вошло 4 эксперимента на сброс и 3 эксперимента на наброс нагрузки, а изменение расхода топлива изображено на рис. 7.
В табл. 2 приведены меры адекватности модели по критерию Тейла, а на рисунках 8 и 9 изображены полученные результаты.
Заключение
Из полученных результатов видно, что у нейросетевой модели есть некоторые расхождения в статичексом режиме по сравнению со сложной поэлементной моделью, предоставленной ОАО «Авиадвигатель». Однако, после обучения модель, построенная на базе нейронной сети, работает гораздо быстрее сложной поэлементной модели, а это значительно упрощает процесс настройки регулятора. К тому же для настройки регулятора нам не обязательно абсолютное совпадение переходных характеристик, достаточно повторение динамики в пределах, задаваемых критерием Тейла, а динамика сравниваемых моделей, как видно из рисунков, практически совпадает. Соответственно в статье представлена быстродействующая модель ГТЭС, на которой становится возможно произвести предварительную настройку регуляторов ГТУ за приемлемое время. Окончательная проверка настройки регуляторов САУ производится при натурных испытаниях ГТЭС на специализированных стендах [2].



