Из существующих характеристик, отражающих уровень опасности при обращении с взрывчатыми веществами (ВВ), можно выделить чувствительность к трению, электрическому разряду, тепловым импульсам и удару. Высокий уровень опасности представляет ударное механическое воздействие на материал. Существует несколько показателей, отражающих чувствительность к удару, среди которых наибольшее распространение получило значение высоты падения ВВ массой 2,5 кг, при котором наблюдается детонация с вероятностью 50 %, характеризует чувствительность вещества и обозначается h50. Работы по прогнозированию данной величины осуществлялись как с применением нейронных сетей [1], так и заданным математическим выражением [4]. В качестве входных данных для нейронных сетей служили молекулярные дескрипторы, энергетические и физические характеристики определенных групп взрывчатых веществ.
Цель данной работы заключается в исследовании возможности прогноза h50 на основе атомарного состава ВВ и сравнение результатов прогноза для генеральной выборки и групп, выделенных по определенному алгоритму.
В качестве исходных данных взята информация о чувствительности h50 226 ВВ с различной молекулярной структурой, рассмотренных в ряде статей [2, 3, 5, 6, 8]. Исходные данные представляют собой химические соединения с общей формулой CaHbNcOd, где индексы варьировались в пределах: 1 ≤ a ≤ 24, 0 ≤ b ≤ 18, 2 ≤ c ≤ 18, 2 ≤ d ≤ 28. Для исследования выбраны различные нитроароматические, нитроалифатические соединения и нитрамины.
Для исследования связи между характеристиками рассчитывались коэффициенты корреляции R между признаками и выходной величиной, а также непосредственно между дескрипторами – Ri.
Учитывая значения коэффициентов корреляции между чувствительностью к удару h50 и различными простыми выражениями типа C/O, (C + H)/O и т.д., получены эмпирические признаки AM1, AM2 и AM3:
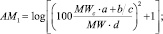 (1)
(1)
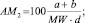 (2)
(2)
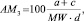 (3)
(3)
где AM1, AM2, AM3 – атомарно-молекулярные дескрипторы; MW – молекулярная масса ВВ; MWС – молекулярная масса углерода; a, b, c, d – число атомов в молекуле CaHbNcOd.
Следует отметить невысокую корреляцию между данными параметрами и кислородным балансом Ob, что позволяет использовать их совместно при расчетах. Выборочные числовые значения коэффициентов корреляции приведены в табл. 1.
Применение нейронных сетей для прогноза чувствительности к удару по всей базе веществ не приводит к удовлетворительным результатам. Для уменьшения ошибки прогноза принято решение о разбиении всей выборки на несколько частей с учётом различных наборов признаков.
Разбиение данных проводилось с помощью процедур кластерного анализа. Применение метода ближнего соседа, дальнего соседа и других аналогичных приводит к последовательному объединению объектов и, соответственно, невозможности выделения нескольких множеств. Среди различных алгоритмов выделения групп выбран метод Уорда [7], т.к. результатом его работы является разбиение на четко выраженные кластеры. Сформированные группы N1 и N2 представлены на рис. 1. В качестве характеристики близости объектов выбрано евклидово расстояние, а в качестве входных признаков рассматривались AM1(выражение (1)), AM1·AM2, (C + H)/O, (C + H)/(N + O), O/MW и Ob.
В результате группировки получены данные по связи признака AM1 и h50. Так при значениях данного параметра, больших 2, для всех веществ характерна низкая чувствительность к удару ≈ 300 см.
Распределение объектов в группах по исследуемому параметру представлено на рис. 2.
Как видно из графика, во вторую группу вошли взрывчатые вещества с высокой чувствительностью h50. Для первой группы характерно наличие объектов во всем диапазоне исследуемого параметра и снижение коэффициента корреляции, что указывает на необходимость дальнейшего разбиения на подмножества в данном кластере. Для второй группы коэффициент корреляции между параметрами увеличился до 0,892, что с учётом существенного сужения диапазона h50 приводит к снижению абсолютной ошибки прогноза.
Таблица 1
Значения выборочных коэффициентов корреляции для генеральной совокупности
|
AM1 |
AM2 |
AM1·AM2 |
(C + N)/O |
(C + H)/O |
· · · |
С*H/O |
Ob |
h50 |
lg(h50) |
|
|
AM1 |
1,000 |
0,788 |
0,793 |
0,712 |
0,710 |
· · · |
0,172 |
–0,749 |
0,574 |
0,652 |
|
AM2 |
0,788 |
1,000 |
0,897 |
0,644 |
0,790 |
· · · |
0,213 |
–0,481 |
0,519 |
0,503 |
|
AM1·AM2 |
0,793 |
0,897 |
1,000 |
0,790 |
0,721 |
· · · |
0,169 |
–0,462 |
0,524 |
0,472 |
|
C/O |
0,710 |
0,432 |
0,570 |
0,856 |
0,761 |
· · · |
0,583 |
–0,890 |
0,564 |
0,631 |
|
(C + N)/O |
0,712 |
0,644 |
0,790 |
1,000 |
0,815 |
· · · |
0,445 |
–0,698 |
0,563 |
0,572 |
|
(C + H)/O |
0,710 |
0,790 |
0,721 |
0,815 |
1,000 |
· · · |
0,710 |
–0,792 |
0,600 |
0,649 |
|
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
· · · |
|
С*H/O |
0,172 |
0,213 |
0,169 |
0,445 |
0,710 |
· · · |
1,000 |
–0,647 |
0,411 |
0,490 |
|
Ob |
–0,749 |
–0,481 |
–0,462 |
–0,698 |
–0,792 |
· · · |
–0,647 |
1,000 |
–0,603 |
–0,758 |
|
h50 |
0,574 |
0,519 |
0,524 |
0,563 |
0,600 |
· · · |
0,411 |
–0,603 |
1,000 |
0,882 |
|
lg(h50) |
0,652 |
0,503 |
0,472 |
0,572 |
0,649 |
· · · |
0,490 |
–0,758 |
0,882 |
1,000 |
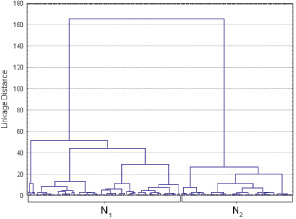
Рис. 1. Дендрограмма для генеральной выборки
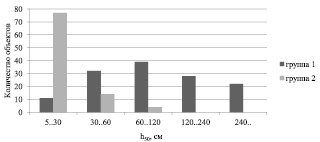
Рис. 2. Распределение веществ в группах по диапазонам чувствительности h50
Таблица 2
Выбор входных параметров для первой группы
|
1,1 |
1,2 |
1,3 |
|
Ri < 0,9 |
Ri < 0,8 |
Ri < 0,8 |
|
R > 0,3 |
R > 0,35 |
R > 0,35 |
|
AM1 AM2 AM3 AM1·AM2 (C + N)/O (C + H)/O (C + H + N)/O O/MW Ob |
AM1·AM2 (C + N)/O (C + H)/O Ob |
AM1 (C + H)/O Ob |
|
h50 |
lg(h50) |
|
Для определения влияния вариаций входных параметров рассматривались коэффициенты взаимной корреляции между дескрипторами и корреляция с h50. В табл. 2 и 3 приведены рассмотренные наборы признаков.
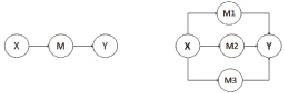
При исследовании рассматривались результаты прогноза нейронными сетями с архитектурой, представленной на рис. 3.
Структура «а» является линейной нейронной сетью с входным слоем данных X, выходным – Y и одним промежуточным слоем M, в котором число нейронов с функцией активации логистического вида варьировалось от 1 до 9. Схема «б» характеризует нейронные сети Уорда с промежуточным слоем из трех блоков. В каждом из блоков используются различные передаточные функции: Гауссова, Гауссова комплементарная и гиперболическая тангенсальная. Количество нейронов между блоками одинаковое, т.к. отклонение от данного соотношения приводит к ухудшению результатов прогноза.
Таблица 3
Выбор входных параметров для второй группы
|
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
|
Ri < 0,9 |
Ri < 0,8 |
Ri < 0,9 |
Ri < 0,8 |
|||
|
R > 0,5 |
R > 0,55 |
R > 0,5 |
R > 0,55 |
|||
|
AM1 AM2 AM1·AM2 C/O (C + N)/O (C + H + N)/O O/MW Ob |
AM1 AM1·AM2 C/O (C + N)/O (C + H + N)/O Ob |
AM1·AM2 (C + N)/O (C + H + N)/O Ob |
AM1 AM1·AM2 C/O (C + N)/O (C + H)/O (C + H + N)/O С/MW O/MWOb |
AM1 AM1·AM2 C/O (C + N)/O (C + H)/O (C + H + N)/O С/MW Ob |
AM1 (C + N)/O (C + H)/O Ob |
(C + N)/O Ob |
|
h50 |
lg(h50) |
|||||
а б
Рис. 3. Рассмотренные архитектуры нейронной сети
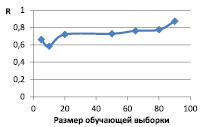
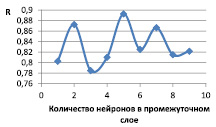
Рис. 4. Графики изменения коэффициента корреляции прогнозируемой величины для второй группы
Изменение коэффициента корреляции в зависимости от количества нейронов в промежуточном слое и размера обучающей выборки для второй группы представлено на рис. 4.
Изменение коэффициента корреляции при увеличении размера промежуточного слоя позволяет выбрать значение, равное 5.
Наилучшие результаты расчета при различных комбинациях дескрипторов получены для следующих условий:
– 1 группа – входные параметры 1,2, выходные параметры – h50; 90 % обучающее множество; архитектура: нейронная сеть Уорда с 5 нейронами в промежуточных блоках.
– 2 группа – входные параметры 2,3, выходные параметры – h50; 80 % обучающее множество; архитектура: последовательная нейронная сеть с 2 нейронами в промежуточном слое.
Прогноз генеральной выборки в целом проводился при входных параметрах – (AM1, C/O, (C + H)/O, (C + H)/(N + O), O/MW, Ob), выходным параметром взят lg(h50); 80 % обучающее множество; архитектура: нейронной сети Уорда с 5 нейронами в промежуточных блоках.
Сравнительные результаты прогноза генеральной выборки и полученных кластеров приведены в табл. 4.
Таблица 4
Показатели погрешности результатов прогноза
|
Данные |
Ср. ошибка, см |
СКО, см |
|
Генеральная выборка |
35,01 |
33,80 |
|
1 группа |
65,45 |
45,54 |
|
2 группа |
5,80 |
3,62 |
Представленные выше данные показывают, что учёт коэффициентов корреляции и выделение групп с помощью процедур кластерного анализа приводит к улучшению результатов прогноза, полученных с помощью нейронных сетей.
В табл. 5 представлены результаты прогноза для некоторых взрывчатых веществ.
Таблица 5
Результаты прогноза чувствительности некоторых ВВ
|
Название |
h50,см |
|
|
Эксп. |
Прогноз |
|
|
2, 4, 6, 8, 10, 12-Hexanitrohexoazaisowurzitane (ε-polymorph) |
12 |
21,17 |
|
Hexanitrobenzene |
11 |
15,08 |
|
Trinitroethylnitroguanidine |
15 |
15,41 |
|
2, 3, 4, 5, 6-Pentonitroaniline |
15 |
20,12 |
|
Benzotrifuroxan |
53 |
50,21 |
|
1, 1, 1, 7, 7, 7-Hexanitroheptanone-4 |
34 |
31,48 |
|
Tetranitrate pentaerythritol |
13 |
16,76 |
|
2`,2`,2`-trinitroethyl-2,4,6-trinitrobenzoate |
24 |
28,80 |
|
Ammonium 3,5-dinitro-1,2,4-triazolate |
110 |
110 |
|
Bis-(trinitroethyl)-oxalate |
15 |
13,77 |
В результате проведенного исследования показана эффективность использования процедур кластерного анализа при прогнозе чувствительности h50. Определено наилучшее сочетание входных признаков, тип и строение нейронной сети. Коэффициент корреляции при расчёте всей базы данных равен 0,785, а для второй группы – 0,892. Отношение средней ошибки результатов расчета и её среднеквадратического отклонения генеральной выборки к выделенной второй группе составило соответственно 6,00 и 9,33. Для получения результатов прогноза генеральной выборки с меньшей погрешностью целесообразно исследовать применение алгоритма разбиения на подгруппы и расширить диапазон изменения характеристик нейронной сети.



