Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лысенко М.В. 1 Лысенко Ю.В. 2 Якушев А.А. 2 Согрина Н.С. 2

---

1 ФГАОУ ВО «Южно-Уральский государственный университет» (Национальный исследовательский университет)»

2 Челябинский филиал ФГБОУ ВО «Финансовый университет при Правительстве Российской Федерации»

В современных условиях на основании требований контроля за движением дебиторской и кредиторской задолженности необходимо использовать моделирование краткосрочных долговых обязательств, что позволит прогнозировать уровень прибыли от продаж с помощью комплексных значений дебиторской и кредиторской задолженности. Оценка адекватности построенной модели осуществляется путем исследования свойств остаточной компоненты, т.е. расхождений, рассчитанных по модели уровней и фактических наблюдений. Так, для проведения статистического анализа временных рядов требуется изучение соотношения между закономерностью и случайностью в формировании значений уровней ряда, оценки количественной меры их влияния, что обосновывает применение определенных научно обоснованных показателей. С целью определения этих показателей необходимо применять метод наименьших квадратов. На основе построенной модели рассчитываются точечные и интервальные прогнозы, данная модель может применяться для прогнозирования «Прибыли от продаж», что является наиболее информативной переменной. Данное основание полагает, что на корреляционную связь зависимой переменной Y с независимыми переменными X1 и Х2 является определение степени влияния дебиторской и кредиторской задолженности на суммарный показатель прибыли от продаж, что приводит к оттоку денежных средств из оборота.

Статья в формате PDF

0 KB

моделирование краткосрочных долговых обязательств

статистического анализа временных рядов

метода наименьших квадратов

точечные и интервальные прогнозы

шкала Чеддока

уровень корреляции

коэффициенты корреляции

1. Анализ финансово-хозяйственной деятельности предприятия: учебное пособие / А.А. Канке, И.П. Кошевая. – М.: ИД ФОРУМ: НИЦ Инфра-М, 2013. – 288 с.

2. Анализ финансово-хозяйственной деятельности: учебник / В.Е. Губин, О.В. Губина. – 2-e изд., перераб. и доп. – М.: ИД ФОРУМ: НИЦ Инфра-М, 2013. – 336 с.

3. Балабанов И.Т. Финансовый менеджмент: учебник. – М.: Финансы и статистика, 2011. – 224 с.

4. Комплексный анализ хозяйственной деятельности предприятия: учебник / Г.В. Савицкая. – М.: НИЦ ИНФРА, 2013. – С. 607.

5. Крылов С.И. Методика анализа дебиторской задолженности по данным бухгалтерской (финансовой) отчетности // Финансовый вестник. – 2011. – № 4. – С. 10–13.

6. Парасоцкая Н.Н. Управление долговыми обязательствами организации // Финансовый вестник. – 2012. – № 1. – С. 7–15.

7. Byul A., Cepel P. SPSS: the art of information processing. The analysis of statistical data and restore hidden patterns: Per. with it. – SPb.: Diasoftyup. 2001. – Р. 40–55.

8. Becker G.S. Human Capital: A Theoretical and Empirical Analysis with Special Reference to Education. – New York, 1993. – 480 p.

9. Gerstenfeld A. Effective Management of Research and Development. Reading. – Mass: Addison–Wesley. 1970. – 320 p.

10. Electronic textbook according to the statistics StatSoft. [Electronic resource]. – The electron. Dan. – Mode of access: www.StatSoft.ru/ home/ textbook.

11. Iberia K. Factor analysis: Per. with it. – M.: Statistics, 1980. – Р. 85–110.

12. Kolemaev C.A., Kalinina C.N. Theory of probability and mathematical statistics: a Textbook. – M.: UNITY-DANA, 2003. – Р. 74–85.

13. Lawley D., Maxwell A. Factor analysis as a statistical method: Per. from English. – M.: Mir, 1967. – Р. 72–130.

Текущее финансовое благополучие предприятия в значительной мере зависит от того, насколько своевременно оно отвечает по своим финансовым обязательствам. Контроль за движением дебиторской и кредиторской задолженности является существенным элементом системы бухгалтерского (финансового) и управленческого учета.

При рациональном управлении предприятием необходимо использовать моделирование краткосрочных долговых обязательств, что позволит прогнозировать уровень прибыли от продаж с помощью значений дебиторской и кредиторской задолженности.

Основная цель статистического анализа временных рядов – изучение соотношения между закономерностью и случайностью в формировании значений уровней ряда, оценка количественной меры их влияния. Закономерности, объясняющие динамику показателя в прошлом, используются для прогнозирования значений в будущем, а учет случайности позволяет определить вероятность отклонения от закономерного развития его возможную величину [7, 9].

Анализ временных рядов, отражающих развитие экономических процессов, начинается с оценки данных. Уровни исследуемого показателя обязательно должны быть сопоставимы, однородны и устойчивы, а число их должно быть достаточно велико.

Оценка параметров модели выполняется с помощью метода наименьших квадратов.

Важным этапом прогнозирования экономических процессов является проверка адекватности модели по реальному явлению. Оценка адекватности построенных моделей осуществляется путем исследования свойств остаточной компоненты, т.е. расхождений, рассчитанных по модели уровней и фактических наблюдений.

На основе построенной модели рассчитываются точечные и интервальные прогнозы. Точечный прогноз на основе временных моделей получается путем постановки в модель (уравнение тренда) соответствующего значения фактора «время». Интервальные прогнозы строятся на основе точечных [8].

Таким образом, организация эффективного управления дебиторской и кредиторской задолженностью позволит контролировать состояние расчетов с дебиторами и кредиторами, снижать риск невозврата дебиторской задолженности и образования просроченной задолженности, своевременно определять потребность в дополнительных ресурсах для покрытия задолженности, вырабатывать рациональную политику предоставления кредитов, что приведет к улучшению финансового состояния предприятия.

Так, в современных условиях и при большой доле постоянных затрат для сокращения показателей дебиторской и кредиторской задолженности предприятию следует проводить прогнозирование краткосрочных долговых обязательств с целью определения возможных сроков инвестирования и потребности денежных средств.

Расчеты дебиторской и кредиторской задолженности на перспективу ведутся на основе бюджета денежных поступлений и оттока денежных средств, связанных с основной производственно-сбытовой деятельностью, и данных финансовой отчетности о движении денежных средств.

Данные об остатке денежных средств на 1 квартал получают из баланса предприятия на начало года. Конечное сальдо 1 квартала становится начальным остатком денежных средств 2 квартала и т.д.

По данным внутренней финансовой отчетности по кварталам за 2013–2015 гг. составлена экономико-математическая модель, которая дает возможность эффективного прогнозирования потока денежных средств предприятия. Основной целью является определение степени влияния дебиторской и кредиторской задолженностей на суммарный показатель прибыли от продаж за период с I квартала 2013 г. по IV квартал 2015 г. Итогом данного исследования явилось оперативное прогнозирование прибыли от продаж на четыре квартала i года.

На основе корреляционного анализа выполнен предварительный анализ данных следующих показателей финансовой деятельности по кварталам за период с 2013 по 2015 г.:

– прибыль от продаж Y – зависимая переменная;

– дебиторская задолженность х1 – независимая переменная;

– кредиторская задолженность х2 – независимая переменная.

В ходе корреляционного анализа были получены следующие данные, отраженные в табл. 1–3.

Качественная оценка парных коэффициентов корреляции выполняется с помощью шкалы Чеддока [10]. Главная цель анализа данных табл. 2 состоит в выявлении корреляционной связи зависимой переменной Y с независимыми переменными X1 и Х2, также выявление независимых переменных, имеющих высокий уровень корреляции между собой.

Таблица 1

Матрица парных корреляций

Таблица 2

Матрица частных корреляций

Таблица 3

Множественные корреляции

Критическое значение коэффициента корреляции при гарантийной вероятности 95 % равно rкр = 0,498. Это означает, что все коэффициенты корреляции, значения которых меньше rкр, принимаются равными нулю, связь между этими признаками считается незначимой, т.е. взаимное влияние признаков отсутствует.

На уровень прибыли от продаж положительное влияние оказывает дебиторская задолженность (ryx1 = 0,095), и она является независимой переменной, кредиторская задолженность оказывает отрицательное влияние (ryx2 = –0,043), так как приводит к оттоку денежных средств из оборота.

По данным табл. 2 видна независимость переменных Х1 и Х2 между собой (rx1x2 = –0,767). Это очень существенно для построения модели регрессии, т.к. отсутствие взаимного влияния между независимыми переменными Х1 и Х2 позволяет включить их в следующий этап исследования – построение модели регрессии.

Анализ данных табл. 3 позволяет сделать вывод о значимости множественного коэффициента корреляции уровня итогового показателя прибыли от продаж от всей совокупности факторов, рассматриваемых в исследовании (Ryx1x2 = 0,768). Данный вывод подтверждается тем, что расчетное значение критерия Фишера Fрасч = 4,832 больше табличного Fтабл(α = 0,05, k1 = 3, k2 = 7) = 4,35.

Таким образом, дебиторская и кредиторская задолженности оказывают незначительное влияние на итоговый показатель прибыли от продаж, т.е. для построения регрессионной модели целесообразно включить оба фактора – дебиторскую и кредиторскую задолженность.

С помощью пакета прикладных программ SPSS:Statistica 6.0 был проведен линейный регрессионный анализ и прогнозирование показателя прибыли от продаж (табл. 4–7).

Таблица 4

Оценка коэффициентов линейной регрессии

На основании данных табл. 4 модель изменения прибыли от продаж от изменения значений факторов Х1 и Х2 имеет вид

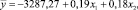
где 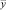– модельные значения прибыли от продаж; х1 – дебиторская задолженность; х2 – кредиторская задолженность.

Параметры модели (а0, а1 и а2) значимы, т.к. их расчетные значения критерия Стьюдента tтабл (табл. 5) больше критического (табличного) значения tтабл(α = 0,2, k = 8) = 1,109.

Включенные в модель факторы Х1 и Х2 на 97 % описывают изменения прибыли от продаж – коэффициент множественной детерминации равен 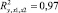(табл. 6). Это свидетельствует о высоком качестве модели, т.е. изменение прибыли на 97 % обусловлено факторами, включенными в модель. Коэффициент множественной детерминации значим, расчетное значение критерия Фишера Fрасч больше табличного Fтабл: Fрасч = 83,3 > Fтабл(α = 0,05, k1 = 3, k2 = 8) = 4,07. Данный факт подтверждает правильность выбора факторов для описания изменения уровня прибыли.

Анализ коэффициентов эластичности, бета-коэффициентов и дельта-коэффициентов позволяет (табл. 4):

1. При отклонении значения фактора на 1 % от своего среднего значения приводит к отклонению прибыли от продаж на величину:

Э1 = 1,953 % для дебиторской задолженности;

Э2 = 1,381 % для кредиторской задолженности;

2. При вариации значений фактора на одно среднеквадратическое отклонение приводит к отклонению прибыли от своего среднего на величину:

β1 = 1,953 ее среднеквадратического отклонения для дебиторской задолженности;

β2 = 1,381 ее среднеквадратического отклонения для кредиторской задолженности;

3. Дельта-коэффициент дебиторской и кредиторской задолженности имеет значение 6,7 и 6,8 %.

Изменение прибыли от продаж определяется изменением значений дебиторской и кредиторской задолженности.

Для оценки качества модели необходимо доказать ее адекватность. Доказательство адекватности модели осуществляется путем оценки свойств остаточной компоненты:

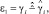
где ε_i – i-е значение остаточной компоненты; yi – i-е фактическое значение прибыли от продаж; 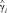i-е значение уровня прибыли от продаж, полученное с помощью модели.

Значения остаточной компоненты представлены в табл. 5, ее характеристики – в табл. 6.

Оценим свойства остаточной компоненты:

1. Математическое ожидание остаточной компоненты равно нулю, т.е. m_ε= –48,077, примерно равно 0 (табл. 5). Свойство выполняется.

2. Уровни остаточной компоненты не коррелированы между собой, т.к. расчетное значение критерия Дарбина – Уотсона dрасч (табл. 6) больше верхней границы d2 табличного (d1 = 0,812; d2 = 1,597):

dрасч = 2,55 > d2 = 1,597.

Табличные значения критерия получены при уровне значимости α = 0,05, числе объясняющих переменных р = 2 и числе уровней остаточной компоненты n = 12. Свойство выполняется.

3. Уровни остаточной компоненты ε носят случайный характер, т.к. Pфакт > Ррасч, где Рфакт = 5 – количество «пиков», которые определяются по значениям остаточной компоненты (столбец абсолютных значений уровней остаточной компоненты табл. 5);

Ррасч = 4 – расчетное значение количества «пиков», которое определяется по формуле

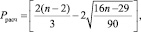
где n = 12 – число уровней временного ряда остаточной компоненты.

4. Уровни остаточной компоненты ε не распределены по нормальному закону, т.к. не выполняется требование:

RSpac = 0,76 не входит в промежуток [RSн = 2,8; RSв = 3,78].

Расчетное значение RS-критерия определяется по формуле

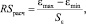
где ε_max = 18,65; ε_min = –34,25 – максимальное и минимальное значения уровней остаточной компоненты (столбец абсолютных значений уровней остаточной компоненты табл. 5); 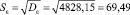– среднеквадратическое отклонение остаточной компоненты, как корень квадратный из дисперсии, значение которой находится в табл. 6.

Вывод: модель статистически неадекватна.

Таблица 5

Значения остаточной компоненты

Таблица 6

Значения остаточной компоненты

Так как полученное уравнение регрессии

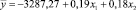
имеет высокий уровень точности, т.к. средняя относительная ошибка остаточной компоненты составляет всего 18,49 %, а значение критерия точности составляет 82,00 % (табл. 6), то данная модель может применяться для прогнозирования «Прибыли от продаж».

С помощью модели (изменения прибыли от продаж от изменения значений факторов Х1 и Х2) выполнено прогнозирование уровня прибыли от продаж. Результаты прогнозирования представлены в табл. 7.

Таблица 7

Прогнозы уровня прибыли

С вероятностью 0,95 можно утверждать, что:

– в I квартале in года значение прибыли от продаж составит 1232,60 тыс. руб., что обеспечит темп роста к IV кварталу in года в 43,90 %.

– в II квартале in года значение прибыли от продаж составит 1389,95 тыс. руб., что выше, чем в предыдущем квартале на 12,8 %.

– в III квартале in года прибыль от продаж составит 1484,57 тыс. руб., что выше, чем в предыдущем квартале, на 6,8 %.

– в IV квартале in года прибыль от продаж составит 1537,55 тыс. руб.

Экономико-математическое моделирование позволит оперативно спрогнозировать прибыль от продаж при изменении показателей дебиторской и кредиторской задолженности.

Оптимизированные бизнес-процессы управления денежными потоками закрепляются в регламентных документах, которые утверждаются внутренним приказом и являются обязательными к исполнению всеми подразделениями. Внутренний документ обязательно должен содержать информацию о порядке прохождения заявок на оплату, сроках, ответственных за согласование, обязанностях и полномочиях сотрудников, последовательности действий [12, 13].

Каждая заявка проходит три уровня контроля. Руководитель центра финансовой ответственности проверяет целесообразность и обоснованность данного расхода, сотрудник отдела планирования и бюджетирования – наличие лимитов в бюджете центра финансовой ответственности на этот вид расхода в данном периоде, сотрудник бухгалтерии – правильность оформления документов на оплату и отсутствие задолженностей по расчетам и представлению документов по данному контрагенту и сотруднику. На все проверки по внеочередным заявкам отводится два часа, по очередным – до двух рабочих дней. После этого заявка в зависимости от суммы и кодировки бюджета попадает к директору, который принимает решение об оплате. Затем заявка направляется в бухгалтерию, которая в зависимости от времени поступления и очередности оплачивает ее в тот же день либо на следующий [11].

Чтобы избежать кассовых разрывов, целесообразно ранжировать все платежи по степени их приоритетности или значимости. Статьи с наиболее высоким приоритетом оплачиваются в обязательном порядке, статьи с пониженным приоритетом – при выполнении дополнительных условий. Можно предложить следующий регламент определения приоритета платежей:

– приоритет первой очереди – платежи, задержка по которым может вызвать серьезные негативные последствия для предприятия. Данный вид платежей оплачивается строго в соответствии со сроком платежа, указанным в заявке;

– приоритет второй очереди – платежи, по которым допустима задержка оплаты на срок до трех рабочих дней без серьезных негативных последствий;

– приоритет третьей очереди – платежи, по которым допустим перенос сроков оплаты более чем на три рабочих дня. При невыполнении плана поступлений по выручке финансовая служба имеет право инициировать сокращение таких статей в бюджете или отмену таких платежей. Если финансовая служба изменила сроки платежа, указанные его инициатором в заявке на оплату, то она обязательно извещает инициатора об этом.

Основным документом, определяющим величину и структуру платежей в текущем периоде, является платежный баланс. Он формируется на каждый календарный месяц плановым отделом на основании представленных соответствующими службами данных о планируемых объемах и условиях продаж продукции, закупок сырья и материалов, об объемах основного и вспомогательного производств, о фонде оплаты труда, начислении налогов и т.д. Платежный баланс предусматривает как суммы первоочередных платежей, так и суммы выплат, относящихся ко второй очереди и др.

Библиографическая ссылка