Магистральный трубопровод, эксплуатируемый в инженерно-геологических условиях 3-й категории сложности, подвержен постоянным изменениям пространственного положения [2–15]. Эти изменения являются компенсацией продольных напряжений, возникающих при смене основных параметров режима работы трубопровода (давление и температура) и обусловлены низкой защемляющей способностью грунтов.
Эксплуатирующая организация имеет возможность отслеживать изменения пространственного положения при помощи инструментальных методов контроля. Однако методы оценки напряженно-деформированного состояния (НДС) трубопровода по фактическим координатам разработаны не в полной мере.
Авторами предлагается методика приближенной оценки напряженно-деформированного состояния условно-прямолинейного участка подземного трубопровода при продольных перемещениях (под перемещениями будем понимать такие деформации, которые не изменяют общую длину участка) и удлинениях (под удлинениями будем понимать такие деформации, которые изменяют суммарную длину участка). Методика позволяет дать оценку сверху величине максимальных эквивалентных напряжений на рассматриваемом участке трубопровода.
Первое, что необходимо сделать, – выяснить, существуют ли в рассматриваемой конструктивной схеме прокладки участка трубопровода (рис. 1, 2) опасные сечения, в которых эквивалентные напряжения принимают максимальные значения. Если они существуют, то НДС всего участка определяется напряжением в опасном сечении. Для этого необходимо доказать, что при любых деформациях справедливо хотя бы одно из неравенств:
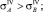
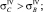 (1)
(1)
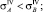
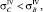 (2)
(2)
где 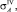
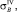
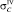 – эквивалентные напряжения в точках А, В, С по 4-й теории прочности.
– эквивалентные напряжения в точках А, В, С по 4-й теории прочности.
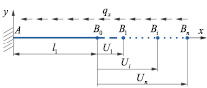
Рис. 1. Расчетная схема к определению НДС условно-прямолинейного участка трубопровода в зависимости от продольного удлинения U
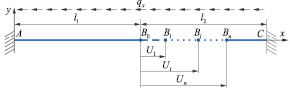
Рис. 2. Расчетная схема к определению НДС прямолинейного участка трубопровода в зависимости от продольного перемещения U
При расчетах НДС подземного трубопровода необходимо учитывать отпор грунта, возникающий при продольных перемещениях и удлинениях. В расчетных схемах (рис. 1, 2) отпор грунта рассчитывается в соответствии с упруго-пластической моделью, предложенной Айбиндером [1]:
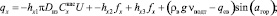 (3)
(3)
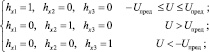 (4)
(4)
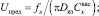 (5)
(5)
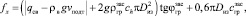 (6)
(6)
где ch – безразмерный коэффициент образования свода обрушения; qсв – собственный вес трубопровода, Н/м; vподт – площадь подтопленного поперечного сечения, м2; Dиз – диаметр трубопровода по изоляции, м; 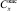 – обобщенный коэффициент касательного сопротивления грунта, Па/м; g = 9,81 м/с2; ρв – плотность воды, кг/м3;
– обобщенный коэффициент касательного сопротивления грунта, Па/м; g = 9,81 м/с2; ρв – плотность воды, кг/м3; 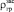 – плотность грунта засыпки, кг/м3;
– плотность грунта засыпки, кг/м3; 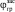 – угол внутреннего трения, град;
– угол внутреннего трения, град; 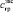 – сцепление грунта засыпки, Па.
– сцепление грунта засыпки, Па.
Составив уравнения равновесия, можно отметить важную особенность: учет сопротивления грунта продольным деформациям трубопровода приводит к уменьшению абсолютного значения дополнительного продольного напряжения в точках A и C и повышению в точке B по сравнению с незащемлённым в грунте трубопроводом:
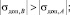 (7)
(7)
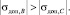 (8)
(8)
Дальнейший вывод проделаем только для участка AB. Для участка BC вывод аналогичен, достаточно лишь учитывать, что знак перемещений изменяется на противоположный.
Распишем эквивалентные напряжения в точках A и В:
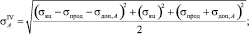 (9)
(9)
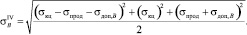 (10)
(10)
Подставив (9) и (10) в (1) и (2) и проведя простейшие преобразования, можно прийти к следующему результату:
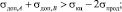 (11)
(11)
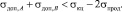 (12)
(12)
Поскольку неравенство (7) требует, чтобы напряжения σдоп,А и σдоп,B были попарно положительными или попарно отрицательными – одно из неравенств (11) или (12) выполняется всегда. Следовательно, в трубопроводе, испытывающем продольные удлинения, всегда есть опасное сечение, которое находится в одной из трех точек: А, В или С.
Из на результатов численных экспериментов и их поточечной аппроксимации авторами получены формулы, позволяющие приближенно оценивать дополнительные продольные напряжения, связанные с продольными удлинениями (13), (14) и перемещениями (13)–(16):
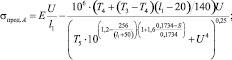 (13)
(13)
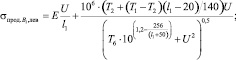 (14)
(14)
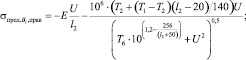 (15)
(15)
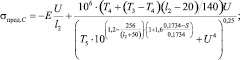 (16)
(16)
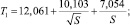 (17)
(17)
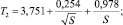 (18)
(18)
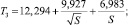 (19)
(19)
T4 = T2; (20)
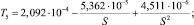 (21)
(21)
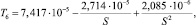 (22)
(22)
где S – площадь поперечного сечения трубопровода, м2; l1, l2 – длина участка в соответствии с рис. 1 и 2, м; U – продольные перемещения, м; E – модуль упругости стали, Па; σпрод.А, σпрод.С – дополнительные продольные напряжения в точках А и С, Па; 
 – дополнительные продольные напряжения слева и справа от точки В, Па.
– дополнительные продольные напряжения слева и справа от точки В, Па.
Получаемые по формулам (13)–(22) результаты можно использовать для расчетов эквивалентных напряжений по формулам (9)–(10).
Ниже изображены графики эквивалентных напряжений, рассчитанные по формулам (9)–(10), (13)–(22) для продольных удлинений (рис. 3) и продольных перемещений (рис. 4) при следующих исходных данных:
Диаметр: D = 1,22 м.
Толщина стенки: δm = 0,025 м.
Внутреннее давление: P = 6 МПа.
Температура трубопровода при строительстве: Tнач = –20 °С.
Температура перекачиваемого продукта: Tкон = 30 °С.
Модуль упругости стали: E = 2,06·1011 Па.
Коэффициент Пуассона стали: μ = 0,3.
Коэффициент линейного температурного расширения стали: α = 1,2·10–5 1/°С.
Можно заметить, что формулы (13)–(22) не содержат в себе физико-механических характеристик грунтов. Это связано с тем, что данные формулы дают оценку сверху для дополнительных продольных напряжений, а следовательно, физико-механические характеристики грунтов были подобраны таким образом, чтобы обеспечить максимальные эквивалентные напряжения.
Выводы
Показано, что магистральные трубопроводы, проложенные в инженерно-геологических условиях 3-й категории сложности, образуют с грунтами динамическую систему. Их пространственное положение непрерывно изменяется и зависит от режима эксплуатации трубопровода. Для оценки сверху величины дополнительных продольных напряжений выполнено доказательство существования наиболее опасных сечений по эквивалентным напряжениям и получены формулы, определяющие дополнительные продольные напряжения в этих сечениях.
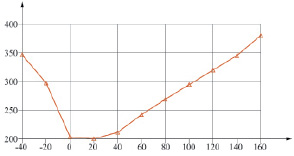
Рис. 3. Зависимость максимальных эквивалентных напряжений от продольных удлинений (расчетная схема соответствует рис. 1) для участка длиной l1 = 160 м
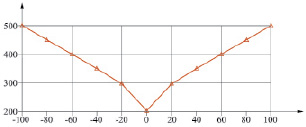
Рис. 4. Зависимость максимальных эквивалентных напряжений от продольных перемещений (расчетная схема соответствует рис. 2) для участка с длинами l1 = 80 м, l2 = 80 м
Библиографическая ссылка
Пульников С.А., Лазарев С.А. ОЦЕНКА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПРЯМОЛИНЕЙНОГО УЧАСТКА ТРУБОПРОВОДА ПРИ МОНИТОРИНГЕ ПЛАНОВО-ВЫСОТНОГО ПОЛОЖЕНИЯ // Фундаментальные исследования. 2016. № 4-2. С. 311-315;URL: https://fundamental-research.ru/ru/article/view?id=40173 (дата обращения: 21.02.2026).



