В [1–4] представлен обзор публикаций, в которых приводятся результаты исследования реологических свойств некоторых видов суспензий на основе мелкодисперсных частиц, демонстрирующих проявление эффекта «отвердевания». В [1] предложена реологическая модель жидкостей такого рода, а в [2] с привлечением этой реологической модели решена задача о течении в цилиндрическом канале. При этом показано, что в зависимости от перепада давления на длине канала возможны три схемы течения. В [3, 4] для первых двух схем течения проведено математическое моделирование конвективного теплопереноса в цилиндрическом канале с учетом диссипации механической энергии. В данной работе приводятся результаты моделирования конвективного теплопереноса с учетом диссипации для третьей схемы течения.
В работе [2] было показано, что третья схема течения реализуется при выполнении следующего условия
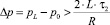 ,
,
где Δp – перепад давления на длине канала; p0, pL – давление на входе и выходе из канала; τ2 – параметр реологической модели суспензии, представляющий собой предельное значение касательного напряжения; L – длина канала; R – радиус канала.
Особенностью такой схемы является формирование в канале трех зон. Первые две из них представляют собой зоны соответственно псевдопластического и дилатантного течения. Третья же зона оказывается заполненной «отвердевшей» жидкостью. Границами раздела между этими зонами являются цилиндрические поверхности с радиусами [2]
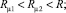
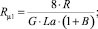
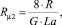
где G, La – геометрический критерий подобия и критерий подобия Лагранжа соответственно; B – параметр реологической модели.
Рассмотрим задачу конвективного теплопереноса в цилиндрическом канале с учетом диссипации механической энергии в случае реализации третьей схемы течения жидкости с эффектом «отвердевания», представленной на рис. 1.
Учитывая разбиение области течения на три зоны, решение задачи по определению распределения температуры в канале будем искать в виде
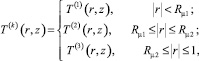
где T(k) (r, z) – распределения температур жидкости в основных зонах, представляющие собой неизвестные функции радиальной r и продольной z координат. Здесь и далее верхний индекс k в круглых скобках принимает значения k = 1, 2, 3 соответственно, для каждой из зон течения с тем же номером.
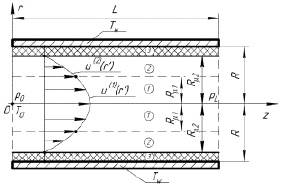
Рис. 1. Третья схема течения: 1, 2, – соответственно первая и вторая зоны течения; 3 – третья зона, заполненная материалом «отвердевшей» жидкости
Решение задачи проводилось в безразмерном виде, с учетом соотношений из [2, 3].
Уравнение конвективного теплопереноса в цилиндрическом канале [5] с учетом диссипации в безразмерном виде для первой и второй зон течения может быть записано следующим образом:
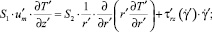 (1)
(1)
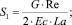
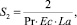
где 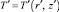 – температура жидкости в канале, представляющая собой неизвестную функцию радиальной r′ и продольной z′ координат;
– температура жидкости в канале, представляющая собой неизвестную функцию радиальной r′ и продольной z′ координат; 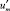 – средняя скорость по проходному сечению канала (с учетом наличия третьей зоны); S1, S2 – параметры уравнения, определяемые через основные критерии подобия;
– средняя скорость по проходному сечению канала (с учетом наличия третьей зоны); S1, S2 – параметры уравнения, определяемые через основные критерии подобия; 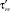 – касательное напряжение;
– касательное напряжение; 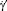 – скорость сдвига; Pr, Ec, Re – критерии подобия Прандтля, Эккерта и Рейнольдса соответственно.
– скорость сдвига; Pr, Ec, Re – критерии подобия Прандтля, Эккерта и Рейнольдса соответственно.
Здесь и далее верхним штрихом обозначены безразмерные величины.
Решение задачи проводили с учетом следующих граничных условий:
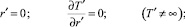 (2)
(2)
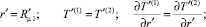 (3)
(3)
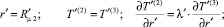 (4)
(4)
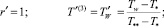 (5)
(5)
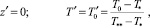 (6)
(6)
где T0 – температура жидкости на входе в канал; Tw – принимаемая постоянной температура стенки канала; T*, T** – некоторые характерные значения температуры среды в канале; λ′ – безразмерный параметр, равный отношению коэффициента теплопроводности «отвердевшей» жидкости к коэффициенту теплопроводности среды во второй зоне.
Применяя методику решения аналогичной задачи [3, 4] для первой и второй зон течения с учетом граничных условий (2), (3), функцию распределения температуры можно представить в виде
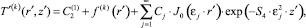 k = 1, 2, (7)
k = 1, 2, (7)
где J0(εj, r′) – функция Бесселя первого рода нулевого порядка; Cj – коэффициенты разложения; 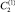 – неизвестная пока константа.
– неизвестная пока константа.
Для краткости записи в (7) приняты следующие обозначения:
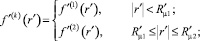
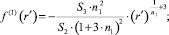
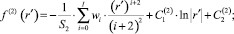
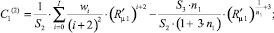
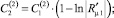
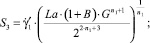
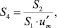
где wi – коэффициенты интерполирующего, степенного по радиальной координате, полинома порядка I, которым представлена диссипативная функция внутри второй зоны течения.
Распределение температуры в канале для третьей зоны должно удовлетворять уравнению
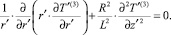 (8)
(8)
Сделаем следующее допущение относительно соотношения плотностей тепловых потоков в направлениях осей z и r:
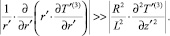 (9)
(9)
Решая тогда уравнение (8) с учетом допущения (9) и граничного условия (5), получаем следующее выражение для распределения температуры в третьей зоне:
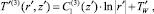 (10)
(10)
где 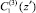 – константа интегрирования, представляющая собой неизвестную пока функцию продольной координаты.
– константа интегрирования, представляющая собой неизвестную пока функцию продольной координаты.
Для определения неизвестных констант интегрирования 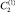 и
и 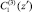 воспользуемся граничными условиями (4).
воспользуемся граничными условиями (4).
Из условия «сшивания» температур на границе второй и третьей зон получаем
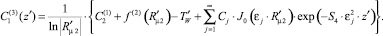
Выполнение условия «сшивания» тепловых потоков на этой же границе раздела зон приводит к следующему соотношению:
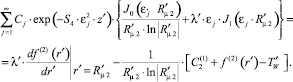
Поскольку это соотношение должно выполняться для любых значений 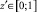 , приходим отсюда к уравнениям
, приходим отсюда к уравнениям
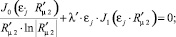 (11)
(11)
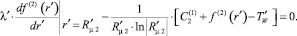 (12)
(12)
Соотношение (11) представляет собой характеристическое уравнение для рассматриваемой краевой задачи и позволяет определить набор значений εj. Решение этого характеристического уравнения проводили численно с привлечением ЭВМ.
Второе же соотношение (12) позволяет найти еще одну константу задачи:
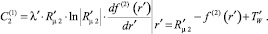 (13)
(13)
Используя условие ортогональности базисных функций, можно показать, что оставшиеся пока неизвестными коэффициенты разложения Cj определяются в виде
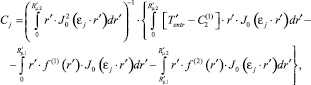 j = 1, 2, ...
j = 1, 2, ...
Таким образом, все константы интегрирования в выражениях (7), (10) для распределения температуры по основным зонам оказываются определенными.
Для оценки влияния параметров математической модели на характеристики диссипативного разогрева среды были проведены численные эксперименты. В ходе расчетов в качестве базовых значений принимался следующий набор безразмерных параметров: B = 0,752; G = 0,133; Pr = 2,476·105; Ec = 1,731·10–6; λ′ = 1; 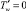 ;
; 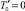 ; при следующих значениях, определенных в [1–4], параметров реологической модели n1 = 0,7;
; при следующих значениях, определенных в [1–4], параметров реологической модели n1 = 0,7;  ; n2 = 0,233, а также пороговых значениях критерия подобия Лагранжа Lacrit1 = 34,247; Lacrit2 = 60. При этом отдельные базовые параметры допускали варьирование своих значений в ходе выполнения численных экспериментов.
; n2 = 0,233, а также пороговых значениях критерия подобия Лагранжа Lacrit1 = 34,247; Lacrit2 = 60. При этом отдельные базовые параметры допускали варьирование своих значений в ходе выполнения численных экспериментов.
Для примера на рис. 2 представлено распределение безразмерной температуры в различных поперечных сечениях канала.
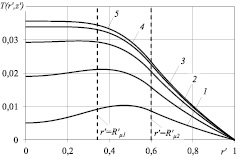
Рис. 2. Распределение безразмерной температуры в различных поперечных сечениях канала при La = 100; Re = 2,07·10–3; для z′ = 0,05 (1); 0,15 (2); 0,3 (3); 0,5 (4); 1 (5)
Штриховыми линиями на этом и следующем рисунках отмечены границы раздела 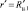 первой и второй зон течения, а также
первой и второй зон течения, а также 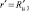 второй зоны течения и третьей зоны, заполненной материалом «отвердевшей» жидкости. Как следует из представленных зависимостей, распределение температуры в поперечном сечении не является монотонным. При этом температурный профиль имеет экстремум типа максимума, который по мере удаления от входного сечения смещается к центру канала.
второй зоны течения и третьей зоны, заполненной материалом «отвердевшей» жидкости. Как следует из представленных зависимостей, распределение температуры в поперечном сечении не является монотонным. При этом температурный профиль имеет экстремум типа максимума, который по мере удаления от входного сечения смещается к центру канала.
Кривые на рис. 3 иллюстрируют влияние критерия подобия Лагранжа на распределение температуры в выходном сечении канала.
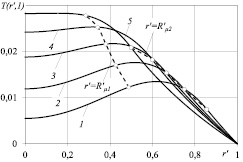
Рис. 3. Распределение безразмерной температуры в выходном сечении канала при Re = 0,01; La = 70 (1); 80 (2); 90 (3); 100 (4); 120 (5)
На рис. 4 для того же, что и на рис. 3, набора числовых значений исходных параметров представлена зависимость радиусов границы раздела первой и второй зон течения, а также границы раздела второй зоны течения и третьей зоны «отвердевшей» жидкости от величины критерия подобия Лагранжа.
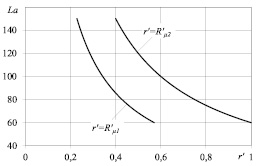
Рис. 4. Влияние критерия подобия Лагранжа на величину радиусов 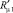 и
и 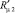
Как видно из представленных на этом рисунке зависимостей, по мере увеличения в указанном диапазоне значений критерия La третья зона расширяется, а соответственно, проходное сечение уменьшается, демонстрируя тем самым проявление эффекта «запирания» канала.
Работа выполнена при поддержке гранта РФФИ, проект № 12-08-00629.
Рецензенты:
Шашкин А.И., д.ф.-м.н., профессор, заведующий кафедрой «Математический и прикладной анализ», ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж;
Буховец А.Г., д.т.н., профессор кафедры «Прикладная математика и применение математических методов в экономике», ФГБОУ ВПО «Воронежский государственный аграрный университет им. императора Петра I», г. Воронеж.
Работа поступила в редакцию 05.08.2014.
Библиографическая ссылка
Колодежнов В.Н., Веретенников А.С. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ДИССИПАТИВНОГО РАЗОГРЕВА В ЦИЛИНДРИЧЕСКОМ КАНАЛЕ ДЛЯ ЖИДКОСТИ С ЭФФЕКТОМ «ОТВЕРДЕВАНИЯ» ПРИ РЕАЛИЗАЦИИ ТРЕТЬЕЙ СХЕМЫ ТЕЧЕНИЯ // Фундаментальные исследования. 2014. № 9-7. С. 1446-1451;URL: https://fundamental-research.ru/ru/article/view?id=35082 (дата обращения: 02.02.2026).



