В современных машинах применяется большое количество механизмов, которые могут быть приведены к кинематической схеме кулисного механизма [1, 5, 6]. В частности широкое применение в грузоподъемных и строительных машинах имеют механизмы с гидро- и пневмоцилиндрами. Исследование динамики таких машин является актуальной задачей. Первым этапом в таких исследованиях является кинематический анализ. В теории механизмов и машин используется несколько методов кинематического анализа. Наибольшее распространение получили метод векторных контуров, разработанный В.А. Зиновьевым [3], метод преобразования координат, развитый в работах Г.Ф. Морошкина [4], а также графические и аналитические методы кинематического анализа плоских механизмов [3, 5, 6].
Целью данной работы является развитие аналитических методов кинематического анализа, а также определение зависимостей между кинематическими параметрами кулисного механизма с одной степенью свободы. В работе приводятся результаты решения частных задач при различных начальных условиях.
Материалы и методы исследования
Рассматривается кулисный механизм (рис. 1) с одной степенью свободы, образованный замкнутой кинематической цепью с тремя подвижными звеньями. Кривошип 1 и кулиса 2 образуют со стойкой неподвижные вращательные кинематические пары O1 и O2.
Исходными данными для кинематического анализа являются длина кривошипа l и координаты неподвижных кинематических пар x1, y1 (пара O1) и x2, y2 (пара O2).
В качестве обобщенных координат рассматриваемой механической системы могут быть выбраны углы поворота кривошипа φ1 и кулисы φ2, а также закон относительного движения кулисного камня S. Связь между этими параметрами можно выразить уравнениями:
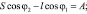 (1)
(1)
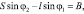 (2)
(2)
где A и B определяются выражениями:
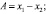
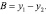
Рассмотрим случай, когда движение механизма задано законом вращения кривошипа, то есть известна зависимость обобщенной координаты φ1 от времени t.
φ1 = φ1(t). (3)
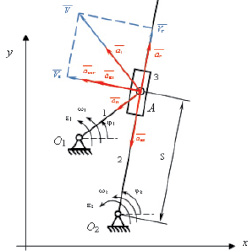
Рис. 1. Кинематическая схема механизма: 1 – кривошип; 2 – кулиса; 3 – кулисный камень
Выражая закон относительного движения кулисного камня S из уравнений (1) и (2), через обобщенную координату φ1, получим кинематическую зависимость
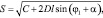 (4)
(4)
где С, D и α определяются выражениями
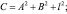
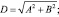
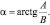
Параметр D – представляет собой расстояние между неподвижными кинематическими парами O1 и O2.
Кинематическая зависимость между углом поворота кулисы и углом поворота кривошипа может определяться по одному из выражений
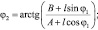 (5)
(5)
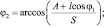 (6)
(6)
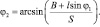 (7)
(7)
Дифференцируя по времени выражения (4) и (5), получим зависимости для относительной скорости кулисного камня Vr и угловой скорости кулисы ω2:
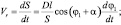 (8)
(8)
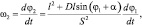 (9)
(9)
где 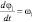 – угловая скорость кривошипа.
– угловая скорость кривошипа.
Скорость кулисного камня в переносном движении Ve, а также его абсолютная скорость Va (рис. 1) определяются выражениями:
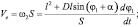 (10)
(10)
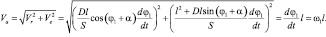 (11)
(11)
Дифференцируя по времени выражения (8) и (9), получим зависимости для относительного ускорения кулисного камня ar и углового ускорения кулисы ε2:
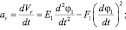 (12)
(12)
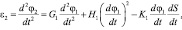 (13)
(13)
где 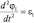 – угловое ускорение кривошипа, а переменные E1, F1, G1, H1 и K1 определяются выражениями:
– угловое ускорение кривошипа, а переменные E1, F1, G1, H1 и K1 определяются выражениями:
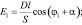
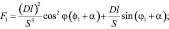
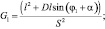
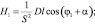
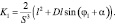
Нормальная 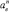 и касательная
и касательная 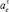 составляющие ускорения кулисного камня в переносном движении, а также ускорение Кориолиса acor (рис. 1) определяются выражениями:
составляющие ускорения кулисного камня в переносном движении, а также ускорение Кориолиса acor (рис. 1) определяются выражениями:
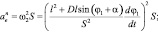 (14)
(14)
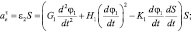 (15)
(15)
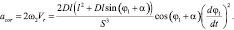 (16)
(16)
Рассмотрим случай, когда движение механизма задано законом относительного движения кулисного камня, то есть известна зависимость обобщенной координаты S от времени t
S = S(t). (17)
К этому случаю сводится большинство задач о движении механизмов с гидро- и пневмоцилиндрами. Кинематическая зависимость угла поворота кривошипа φ1 от расстояния S может быть выражена из уравнений (1) и (2)
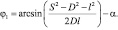 (18)
(18)
Для определения угла поворота кулисы φ2 может использоваться кинематическая зависимость (5), где φ1 определяется выражением (18).
Дифференцируя по времени выражения (18) и (5), получим зависимости для угловых скоростей кривошипа ω1 и кулисы ω2:
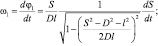 (19)
(19)
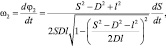 (20)
(20)
где 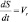 – относительная скорость кулисного камня.
– относительная скорость кулисного камня.
Дифференцируя по времени выражения (19) и (20), получим зависимости для угловых ускорений кривошипа ε1 и кулисы ε2:
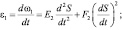 (21)
(21)
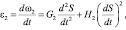 (22)
(22)
где 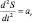 – относительное ускорение кулисного камня, а переменные E2, F2, G2, H2 определяются выражениями:
– относительное ускорение кулисного камня, а переменные E2, F2, G2, H2 определяются выражениями:
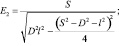
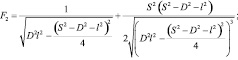
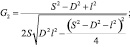
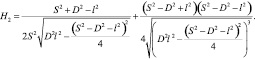
Нормальная 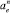 и касательная
и касательная 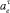 составляющие ускорения кулисного камня в переносном движении, а также ускорение Кориолиса acor, для рассматриваемого случая, определяются выражениями:
составляющие ускорения кулисного камня в переносном движении, а также ускорение Кориолиса acor, для рассматриваемого случая, определяются выражениями:
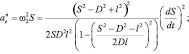 (23)
(23)
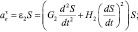 (24)
(24)
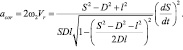 (25)
(25)
Нормальное an и касательное aτ ускорения кулисного камня, а также его полное ускорение a (рис. 1), определяются выражениями:
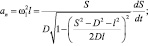 (26)
(26)
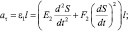 (27)
(27)
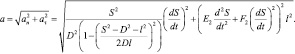 (28)
(28)
Полученные зависимости для кинематических характеристик являются общими для различных законов вращения кривошипа и относительного движения кулисного камня.
Результаты исследования и их обсуждение
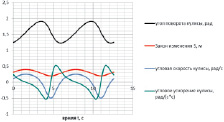
На рис. 2, а представлены зависимости кинематических характеристик механизма от времени в случае равномерного вращения кривошипа с угловой скоростью ω1, равной 1 рад/с, а на рис. 2, б в случае равноускоренного вращения кривошипа с угловым ускорением ε1, равным 0,1 рад/с2.
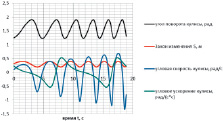
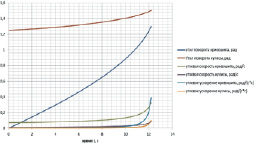
На рис. 3, а представлены зависимости кинематических характеристик механизма от времени в случае равномерного относительного движения кулисного камня со скоростью Vr, равной 0,00664 м/с, а на рис. 3, б в случае равноускоренного относительного движения кулисного камня с ускорением ar, равным 0,001 м/с2.
 а
а
 б
б
Рис. 2. Кинематические характеристики механизма: а – кинематические характеристики при равномерном вращении кривошипа; б – кинематические характеристики при равноускоренном вращении кривошипа
 а
а
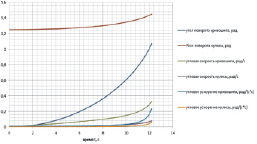 б
б
Рис. 3. Зависимость углов поворота стержней от времени: а – кинематические характеристики при равномерном относительном движении кулисного камня; б – кинематические характеристики при равноускоренном относительном движении кулисного камня
Представленные зависимости получены при следующих исходных данных и начальных условиях:
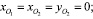
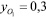 (м);
(м);
l = 0,1 (м); t0 = 0; φ1(t0) = 0.
Заключение
Анализ зависимостей кинематических характеристик от времени (рис. 2), полученных для случая задания движения механизма законом вращения кривошипа, показывает, что кинематические характеристики кулисы (φ2, ω2, ε2), а также кинематические характеристики кулисного камня (S, Vr, ar) носят периодический характер.
В случаях равномерного и равноускоренного движения кулисного камня, анализ зависимостей кинематических характеристик от времени (рис. 3) показывает, что угловые скорости кривошипа ω1 и кулисы ω2, а также угловые ускорения кривошипа ε1 и кулисы ε2 неограниченно возрастают при φ1 = φ2.
Результаты работы могут быть использованы для разработки математических моделей движения кулисных механизмов и разработки алгоритмов автоматизации соответствующих расчетов.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Ваганов А.Б., д.т.н., профессор кафедры «Аэрогидродинамика, прочность машин и сопротивление материалов», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Работа поступила в редакцию 02.06.2014.
Библиографическая ссылка
Смирнов Д.А. КИНЕМАТИЧЕСКИЙ АНАЛИЗ КУЛИСНОГО МЕХАНИЗМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ С НЕПОДВИЖНЫМИ ВРАЩАТЕЛЬНЫМИ КИНЕМАТИЧЕСКИМИ ПАРАМИ // Фундаментальные исследования. 2014. № 8-5. С. 1069-1074;URL: https://fundamental-research.ru/ru/article/view?id=34719 (дата обращения: 31.01.2026).



