В работе [1] была предложена реологическая модель жидкости, которая при определенных значениях скоростей сдвига демонстрирует проявление эффекта «отвердевания». В [2] рассмотрена задача о течении такого рода жидкости в цилиндрическом канале. Там же было показано, что в зависимости от диапазона изменения перепада давления могут быть реализованы три схемы течения. Задача о конвективном теплопереносе для первой схемы течения, когда жидкость всюду внутри канала демонстрирует псевдопластическое поведение со степенным законом вязкости, была рассмотрена в [3]. В данной работе рассматривается подобная задача, но для второй схемы течения.
В [1] было показано, что вторая схема течения реализуется при значениях перепада давления Δp на длине L цилиндрического канала радиуса R, которое удовлетворяет следующему условию:
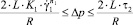 ,
,
где τ2 – константа реологической модели суспензии, представляющая собой предельное значение касательного напряжения; 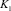 ,
,  ,
, 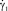 – коэффициент консистенции, индекс течения и пороговое значение скорости сдвига соответственно.
– коэффициент консистенции, индекс течения и пороговое значение скорости сдвига соответственно.
При этом область течения в канале разбивается на две зоны – псевдопластического течения в центральной части и дилатантного в окрестности стенки. Граница раздела между зонами течения представляет собой цилиндрическую поверхность радиуса 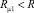 .
.
Дальнейшее увеличение Δp и, соответственно, выполнение условия
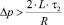
приводит к формированию в окрестности стенки канала третьей зоны течения, заполненной «отвердевшей» жидкостью.
Рассмотрим вторую схему течения в цилиндрическом канале жидкости демонстрирующей эффект «отвердевания». Согласно реологической модели, представленной в [1], в данном случае вязкость жидкости на некотором интервале изменения скорости сдвига уменьшается, а на другом – по мере увеличения модуля скорости сдвига возрастает до некоторого максимального значения.
Решение задачи по нахождению распределения температур с учетом разбиения области течения на зоны предлагается искать в виде
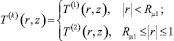 ,
,
где T(k)(r, z) – распределения температур жидкости в зонах течения, представляющие собой неизвестные функции радиальной r и продольной z координат.
Здесь и далее верхний индекс k в круглых скобках принимает значения k = 1 или k = 2 соответственно для первой и второй зон течения.
Решение поставленной задачи проводилось в безразмерном виде, с учетом соотношений, представленных в [3]. При этом гидродинамическая часть задачи решалась отдельно от тепловой. Выражения для распределения скоростей по сечению цилиндрического канала, а также средней скорости и объемного расхода, с учетом разбиения на зоны, представлены в работе [1]. В ходе решения этой части задачи было получено выражение для определения границы раздела зон течения
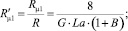
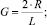
где G, La – геометрический критерий подобия и критерий подобия Лагранжа.
Здесь и далее верхним штрихом обозначены безразмерные величины.
Предполагалось, что конвективный теплоперенос вдоль оси канала допустимо определять по средней скорости  потока. Диссипативную же составляющую принимали с учетом точного распределения скорости [2] в поперечном сечении канала. С учетом этих допущений уравнение конвективного теплопереноса [4] в цилиндрическом канале с учетом диссипации в безразмерной форме может быть представлено в виде
потока. Диссипативную же составляющую принимали с учетом точного распределения скорости [2] в поперечном сечении канала. С учетом этих допущений уравнение конвективного теплопереноса [4] в цилиндрическом канале с учетом диссипации в безразмерной форме может быть представлено в виде
 (1)
(1)
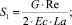
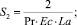
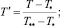
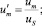
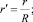
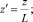
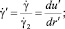
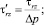
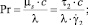
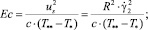
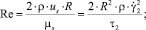
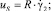
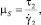
где S1, S2 – параметры уравнения, определяемые через основные критерии подобия; T = T(r, z) – температура жидкости в канале, представляющая собой неизвестную функцию радиальной и продольной координат; τrz, 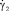 – касательное напряжение и пороговое значение скорости сдвига; T**, T*, uS, μS – некоторые характерные значения температуры среды в канале, а также скорости жидкости и динамической вязкости, принимаемые в качестве масштабных; ρ, c, λ – принимаемые постоянными плотность, теплоемкость, теплопроводность среды соответственно; Pr, Ec, Re – критерии подобия Прандтля, Эккерта и Рейнольдса соответственно.
– касательное напряжение и пороговое значение скорости сдвига; T**, T*, uS, μS – некоторые характерные значения температуры среды в канале, а также скорости жидкости и динамической вязкости, принимаемые в качестве масштабных; ρ, c, λ – принимаемые постоянными плотность, теплоемкость, теплопроводность среды соответственно; Pr, Ec, Re – критерии подобия Прандтля, Эккерта и Рейнольдса соответственно.
С учетом реологической модели [1] выражения для касательных напряжений записываются в виде
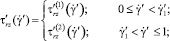
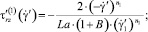
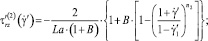
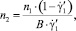
где n2 – параметр реологической модели.
Принимая во внимание полученные выражения для касательных напряжений, диссипативная функция W′(r′) представляется в виде
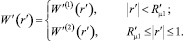
Учитывая выражение для распределения скорости в первой зоне [2], находим
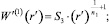
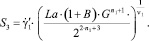
Прямое определение диссипативной функции для второй зоны в аналитическом виде представляется затруднительным. В этой связи представим диссипативную функцию в виде интерполирующего полинома порядка I:
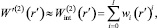
где wi – коэффициенты полинома.
При решении задачи использовались следующие температурные граничные условия:
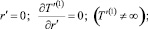 (2)
(2)
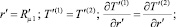 (3)
(3)
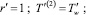 (4)
(4)
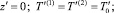 (5)
(5)
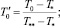
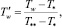
где T0 – температура жидкости на входе в канал; Tw – принимаемая постоянной температура стенки канала.
Решая (1) с учетом граничных условий (2)–(5), распределение температуры в канале может быть представлено в виде
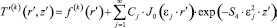 (6)
(6)
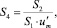
где J0 – функция Бесселя первого рода нулевого порядка [5]; εj – корни характеристического уравнения J0(ε) = 0; Cj – коэффициенты разложения.
Для краткости записи в (6) приняты следующие обозначения:
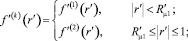
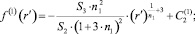
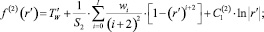
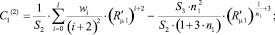
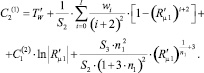
Учитывая условие ортогональности базисных функций, коэффициенты разложения Cj в выражении (6) принимают вид
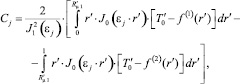
где J1 – функция Бесселя первого рода первого порядка [5].
С полученными выражениями для распределения температуры в канале были проведены численные эксперименты по анализу влияния параметров математической модели на характеристики теплопереноса. В качестве базовых параметров модели были приняты следующие значения: n1 = 0,7; 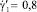 ; B = 0,752; n2 = 0,233; G = 0,133; Pr = 2,476·105; Ec = 1,731·10–6; La = 50; Re = 2,07·10–3;
; B = 0,752; n2 = 0,233; G = 0,133; Pr = 2,476·105; Ec = 1,731·10–6; La = 50; Re = 2,07·10–3; 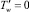 ;
; 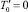 . Заметим, что для данного набора параметров вторая схема течения реализуется при условии изменения критерия подобия Лагранжа в диапазоне от La1 = 34,247 до La2 = 60.
. Заметим, что для данного набора параметров вторая схема течения реализуется при условии изменения критерия подобия Лагранжа в диапазоне от La1 = 34,247 до La2 = 60.
Для примера на рис. 1 представлено распределение безразмерной температуры по радиальной координате в различных поперечных сечениях канала.
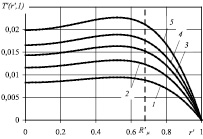
Рис. 1. Распределение безразмерной температуры в различных поперечных сечениях канала для z′ = 0,05 (1); 0,1 (2); 0,2 (3); 0,4 (4); 0,6 (5); 0,8 (6); 1 (7)
Штриховой линией на этом и следующем рисунках отмечена граница раздела  первой и второй зон течения. Из зависимостей, представленных на рис. 1, видно, что по мере течения жидкости по цилиндрическому каналу происходит ее прогрев за счет диссипации механической энергии. При этом наблюдается экстремум температуры, который по мере продвижения жидкости по каналу смещается из второй в первую зону течения.
первой и второй зон течения. Из зависимостей, представленных на рис. 1, видно, что по мере течения жидкости по цилиндрическому каналу происходит ее прогрев за счет диссипации механической энергии. При этом наблюдается экстремум температуры, который по мере продвижения жидкости по каналу смещается из второй в первую зону течения.
На рис. 2 представлено влияние критерия подобия Эккерта на распределение температуры в выходном сечении канала.
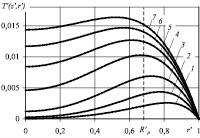
Рис. 2. Влияние критерия подобия Эккерта на распределение температуры в выходном сечении канала при Ec = 1·10–6 (1); 1,4·10–6 (2); 1,731·10–6 (3); 2·10–6 (4); 2,4·10–6 (5)
Из представленных данных следует, что увеличение значений критерия подобия Эккерта приводит к более интенсивному диссипативному разогреву жидкости, который сопровождается появлением пика температуры в первой зоне течения.
Работа выполнена при поддержке гранта РФФИ, проект № 12-08-00629.
Рецензенты:
Шашкин А.И., д.ф.-м.н., профессор, заведующий кафедрой «Математический и прикладной анализ», ГОУ ФБГОУ ВПО «Воронежский государственный университет», г. Воронеж;
Буховец А.Г., д.т.н., профессор кафедры «Прикладная математика и применение математических методов в экономике», ГОУ ФБГОУ ВПО «Воронежский государственный аграрный университет им. императора Петра I», г. Воронеж.
Работа поступила в редакцию 10.12.2013.
Библиографическая ссылка
Колодежнов В.Н., Капранчиков С.С., Веретенников А.С. МОДЕЛИРОВАНИЕ ДИССИПАТИВНОГО РАЗОГРЕВА В ЦИЛИНДРИЧЕСКОМ КАНАЛЕ ДЛЯ ЖИДКОСТИ С ЭФФЕКТОМ «ОТВЕРДЕВАНИЯ» ПРИ РЕАЛИЗАЦИИ ВТОРОЙ СХЕМЫ ТЕЧЕНИЯ // Фундаментальные исследования. 2013. № 11-2. С. 179-183;URL: https://fundamental-research.ru/ru/article/view?id=33093 (дата обращения: 16.02.2026).



