Представление большинства существующих математических моделей систем физической защиты (СФЗ) [3, 4, 7, 9, 11, 12 и др.] произведено методом прямого описания [10], основанного на вероятностных мерах. В то же время решение задачи структурно-параметрического синтеза обуславливает необходимость косвенного описания: представления входных (управляемых) переменных модели СФЗ, составления уравнения связи, учитывающее топологическую структуру СФЗ и позволяющее определить значения выходных параметров [10]. В [5] на основе анализа модели системы безопасности объекта (метасистемы СФЗ) произведена формализация математической модели СФЗ со сложной топологией в виде ориентированного мультиграфа [5]:
S = S(X, Γ, D, H), (1)
где X – конечное множество вершин графа S; Γ – отображение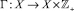 
, заданное конечным подмножеством дуг 
, 
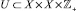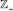– множество неотрицательных целых чисел; D ⊂ X – множество элементов «объект защиты»; H ⊂ X – множество элементов «субъект угрозы».
Предложенное представление ограничивает постановку задачи синтеза до параметрического. Другими словами, на основе сформированной в [5] математической модели возможно решение задачи синтеза, обеспечивающего рациональный набор опций по реализации рубежей защиты – весов ребер орграфа, определяемых из указанного множества «…альтернативных реализаций рубежа защиты …» [5] с учетом заранее заданной топологией СФЗ.
В свою очередь структурно-параметрический синтез комплекса инженерно-технических средств (КИТС) СФЗ предполагает проведение совместного решения задачи нахождения рациональных (с точки зрения заданного критерия эффективности):
1) топологии КИТС СФЗ, определяющей расстановку и смежность между узлами орграфа (подступами к объекту, рубежами защиты и охраняемыми зонами) с учетом ограничения на существование путей (доступа) от подступов до объекта к определенным зонам охраны, т.е. задача структурного синтеза;
2) плана установки на рубежах защиты различных технических средств охраны (ТСО), т. е. задача параметрического синтеза.
Цель статьи заключается в разработке математической модели КИТС СФЗ, позволяющей учесть структурные и функциональные свойства системы физической защиты объекта охраны.
Математическая модель КИТС СФЗ объекта охраны
Представим структуру КИТС СФЗ объекта охраны в виде многоуровневой иерархической системы с сильными связями [8], топология которой задана в виде ориентированного связного графа G(V, E) без петель и кратных рёбер (корневого ориентированного графа с древовидной структурой) [2], представленного совокупностью непустого множества вершин V и множества ребер E двухэлементных подмножеств множества V [8]:
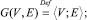
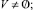
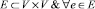
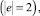(2)
где 
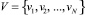, а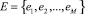 
, 
, 
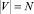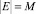(N и M – общее число вершин и ребер графа соответственно).
В соответствии с типом синтезируемой системы множество вершин V графа G(V, E) представим совокупностью трех непересекающихся подмножеств:
1) Vs – подступы к объекту (корни ориентированного дерева);
2) Vp – рубежи защиты (промежуточные вершины ориентированного дерева);
3) Ve – охраняемые зоны (листья ориентированного дерева), где V = Vs ∪ Vp ∪ Ve с условиями: Vs ∩ Vp ∩ Ve = ∩V,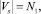 
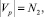
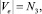N = N1 + N2 + N3.
В рамках рассматриваемой задачи ребра графа задают «правила взаимодействия» между элементами (вершинами графа) иерархической системы, т.е. по существу определяют возможность доступа (пути) нарушителя к охраняемым зонам (вершинам графа). Геометрическое представление ориентированного графа G(V, E) в рассматриваемой постановке задачи отражено на рис. 1.
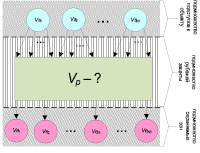
Рис. 1. Геометрическое представление ориентированного графа G(V, E)
Ориентированный граф G(V, E) зададим двумя матрицами инцидентности для прямого и обратного потоков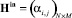 
и 
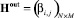соответственно, элементы которых определяются выражениями [13]
(3)
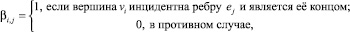(4)
причем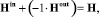 
где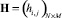 
– общая матрица инцидентности для графа G(V, E). Поскольку решением задачи синтеза структуры иерархической системы является некоторая древовидная структура, то для нахождения оптимальной система должна содержать все возможные орграфы древовидного типа с корнями Vs и висячими вершинами Ve. Будем считать, что корни графа опираются на некоторый полносвязный подграф, построенный на заданном множестве вершин, а листья соединены со всеми вершинами полносвязного подграфа.
С учетом возможной разнородности рубежей защиты подмножество Vp множеств вершин V исходного графа представляется объединением R непересекающихся множеств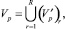 
, где r-е множество 
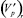определяет совокупность 
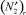рубежей защиты r-го типа, характеризующегося различной степенью защиты от возможных способов преодоления. Последнее задает характеристику i2-х рубежей защиты соответствующих r-м типам в виде матрицы 
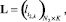(i2, k)-е элементы которого отражают вероятность преодоления i2-го рубежа защиты k-м способом. В свою очередь различные условия расположения подступов к объекту охраны обусловливают неоднородность распределения вероятностей задания пути проникновения злоумышленника через них на охраняемый объект, численно задаваемый исходным вектором 
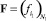– вероятности угрозы со стороны i1-х подступов к объекту охраны.
Формальное представление задачи параметрического синтеза состоит в определении рационального плана установки ТСО на i2-х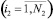 
рубежах защиты. С учетом указанной возможности установки на рубежах ТСО различного класса в исходной постановке задачи задается P типов ТСО, характеризующихся матрицей 
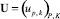и вектором 
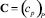стоимости p-го типа ТСО. Элементы матрицы U определяют вероятность защиты p-м ТСО от k-го способа преодоления рубежа злоумышленником. При этом размещение определенного числа ТСО на рубежах защиты ограничено заданным максимальным значением стоимости используемых ресурсов 
.
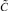Исходная характеристика i3-х охраняемых зон задается вектором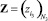 
значимости, i3-е элементы которого численно определяют материальный ущерб от злоумышленника в случае доступа к i3-й зоне охраны. Ограничения на топологическую структуру синтезируемого КИТС СФЗ задается матрицей 
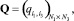элементы которой определяют правило существования пути из i1-го подступа к объекту в i3-ю охраняемую зону:
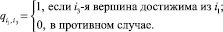(5)
С учетом принятых представлений и сформированной на их основе структурной схемы КИТС СФЗ (рис. 2) произведем описание математической модели КИТС СФЗ путем указания характеристик ее входных и выходных параметров и их математической взаимосвязи. Последнюю представим функциональным оператором Ψ(X, Y, T), преобразующим пространство матриц управляющих переменных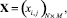 
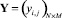и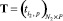 
в выходной параметр, величина которого количественно характеризует заданный критерий эффективности КИТС СФЗ. Элементы матриц управляющих переменных X и Y определяют соответствующие элементы матриц инцидентности для прямого Hin и обратного Hout потоков синтезируемой структуры СФЗ. Элементы матрицы T характеризуют количество устанавливаемых на i2-м рубеже защиты p-х типов ТСО. При этом элементы матриц управляющих переменных X, Y, T могут принимать фиксированные значения, множества которых определяются условиями:
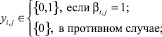(6)
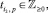(7)
где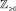 
– множество неотрицательных целых чисел: {0, 1, 2, ...}.
Принятые обозначения позволяют записать обобщенную задачу структурно-параметрического синтеза КИТС СФЗ в виде:
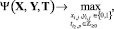(8)
с учетом ограничения на максимально допустимую стоимость устанавливаемых ТСО на i2-х рубежах защиты:
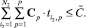(9)
Вышеописанное позволяет разработать обобщенное геометрическое представление задачи структурно-параметрического синтеза КИТС СФЗ (рис. 3).
Сформированное представление позволяет перейти к разработке функциональной зависимости целевой функции (8) от матриц управляемых переменных X, Y, T, определяющей критерий эффективности КИТС СФЗ, заданного по правилу «результативность – стоимость».
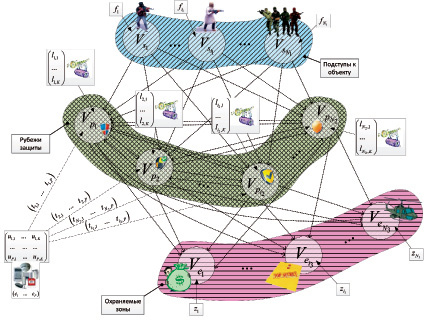
Рис. 2. Структурная схема комплекса инженерно-технических средств системы физической защиты объекта охраны
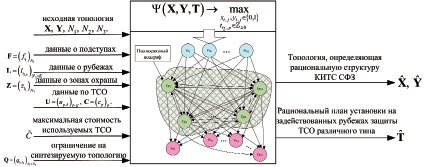
Рис. 3. Геометрия решения задачи структурно-параметрического синтеза системы физической защиты
Критерий оценки эффективности структурно-параметрического синтеза КИТС СФЗ
С целью определения аналитической зависимости целевой функции (8) от матриц управляющих переменных X, Y, T введем следующие представления.
Утверждение 1. Для ориентированного графа G(V, E) без петель и кратных ребер произвольной топологии, заданной двумя матрицами инцидентности для прямого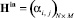 
и обратного 
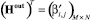потоков, матрица достижимости S(r) для путей длины r ∈ определяется в соответствии с равенством
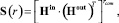(10)
где операция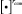 
определяет композицию отношений степени r.
Доказательство. Пусть G(V, E) есть ориентированный граф без петель и кратных ребер, состоящий из N вершин и M дуг, топология которого задана двумя матрицами размерности N×M инцидентности для прямого Hin и обратного Hout потоков. Тогда композиция отношения матрицы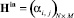 
и транспонированной матрицы 
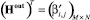будет характеризоваться матрицей 
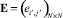, (i′, j′)-й элемент которой определяется в соответствии с отношением
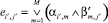. (11)
Поскольку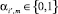 
и 
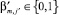определяют инцидентность m-го ребра к i’-й и j’-й вершинам соответственно, очевидно, что элемент 
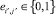матрицы 
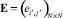для ориентированного графа G(V, E) без петель и кратных ребер в конечном счете задает достижимость вершины i’ к вершине j’ через одно ребро (для пути кратности 1), т.е. по существу определяет смежность вершин i’ и j’.
Тогда в соответствии с теоремой 1.4, доказательство которой представлено в [1], возведение матрицы смежности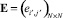 
в натуральную степень r определяет матрицу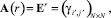 
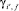-е элементы которой задают число 
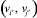– маршрутов длины r, а соответственно композиция отношений степени r над матрицей 
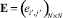определяет матрицу достижимости S(r)для путей длины r ∈ .
Следствие 1 из утверждения 1. В соответствии с выраженим (10) матрица достижимости для всех возможных путей кратности от 1 до R будет задаваться соотношением
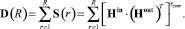(12)
Следствие 2 из утверждения 1. Для ориентированного взвешенного графа G(V, E) без петель и кратных ребер, для которого задан вектор весов ребер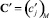 
, матрица смежности 
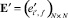определяется равенством
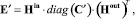(13)
где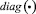 
– оператор преобразования произвольного вектора размерностью N в диагональную матрицу N×N, элементы главной диагонали которой соответствуют элементам исходного вектора, а все остальные элементы (расположенные выше/ниже главной диагонали) равны 0.
С учетом отношений (10), (12), (13) определим искомое аналитическое представление функции Ψ(X, Y, T), задающей обратную величину суммарного вероятного уровня ущерба (риска [14]) КИТС СФЗ, в виде равенства
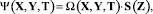(14)
где S(Z) – векторная функция, преобразующая N3 мерный вектор значимости охраняемых зон в вектор размерности N, элементы которого определяют значимость i-й вершины графа (узла СФЗ)
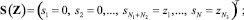
Ω(X, Y, T) – векторная функция, обратная величине действительного риска размерности N, элементы которой задают вероятность защиты от угрозы к i-м узлам КИТС СФЗ с учетом воздействий субъектов защиты (ТСО) на субъект угрозы (злоумышленника), и определяются в соответствии с отношением
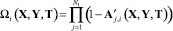(15)
Здесь A′(X, Y, T) – матрица размерности N×N, (i, j)-е, элементы которой задаются в виде:
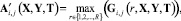(16)
где G(r, X, Y, T) – матричная функция размерности N×N, определяемая рекурсией:
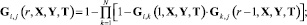
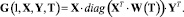(17)
В выражении (16) применение оператора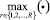 
задает значение максимальной вероятности угрозы для всех возможных путей кратности r. Последнее определяет решение задачи структурно-параметрического синтеза КИТС СФЗ на «наихудший случай», обусловленное необходимостью нахождения оптимального решения в условиях полной априорной неопределённости о стратегии злоумышленника [15].
В выражении (17) W(T) – векторная функция размерности N, i-е элементы которой задаются в соответствии с равенством
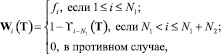(18)
где ϒ(T) – векторная функция размерностью N2, элементы которой характеризуют вероятность препятствованию действиям злоумышленника хотя бы одного ТСО (вероятность появления хотя бы одного события [6]), устанавливаемого на i2-м рубеже защиты, и задаются отношением
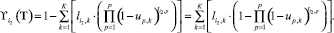(19)
С учетом представлений, рассмотренных выше, критерий эффективности КИТС СФЗ, заданный по правилу «результативность – стоимость» в исходной задаче структурно-параметрического синтеза, примет вид:
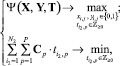(20)
при условии, что:
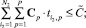
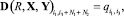(21)
где D(R, X, Y, T) – матрица размерности N×N достижимости всех возможных путей кратности от 1 до R, определяемой в соответствии с выражением (12).
Значение R определяет максимально возможную длину пути в синтезируемой структуре КИТС СФЗ и в первом приближении задается равным числу промежуточных пунктов графа исходной задачи N2 (рубежей защиты).
С целью сведения двухкритериальной задачи (20) к однокритериальной представим обобщенный критерий эффективности КИТС СФЗ в виде отношения максимизируемой функции к минимизируемой:
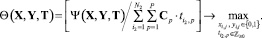(22)
Значение функции Θ(X, Y, T) в выражении (22) аналогично [8] определяет рентабельность СФЗ.
Выводы
Разработана математическая модель КИТС СФЗ, отличающаяся тем, что сформированное представление позволяет учесть структурные и функциональные свойства КИТС СФЗ: структуру (3), (4), определяющую топологические связи между подступами к объекту, рубежами защиты и охраняемыми зонами; k-е способы преодоления рубежей защиты; различие ТСО по принципу действия, обеспечивающих разноэффективный уровень защиты рубежа от известных способов его преодоления; стоимость технических средств охраны; ограничение на допустимую стоимость устанавливаемых технических средств охраны, необходимых для решения задачи по нахождению рациональных топологий КИТС СФЗ и плана установки на рубежах защиты различных ТСО.
На основе произведенной формализации определена аналитическая зависимость (22) критерия оценки эффективности КИТС СФЗ, количественно определяющего его рентабельность, от матриц управляющих переменных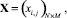 
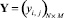и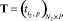 
, элементы которых задают структурную топологию синтезируемой КИТС СФЗ и плана установки на рубежах защиты различных ТСО.
Рецензенты:
Саитов И.А., д.т.н., профессор, сотрудник Академии ФСО России, г. Орел;
Иванов Б.Р., д.т.н., профессор, сотрудник Академии ФСО России, г. Орел.
Работа поступила в редакцию 03.06.2013.
Библиографическая ссылка
Полянский И.С., Беседин И.И., Панин Б.Л. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОМПЛЕКСА ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ СРЕДСТВ СИСТЕМЫ ФИЗИЧЕСКОЙ ЗАЩИТЫ ОБЪЕКТА ОХРАНЫ // Фундаментальные исследования. 2013. № 6-6. С. 1359-1365;URL: https://fundamental-research.ru/ru/article/view?id=31741 (дата обращения: 04.04.2025).