Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Наумова Н.А. 1

---

1 ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ

Предложена вероятностная модель транспортного потока, базирующаяся на гипотезе о распределении интервалов по времени между подряд идущими автомобилями по закону Эрланга, который позволяет описывать потоки высокой плотности. Разработано граф-представление модели, а также приведена структура матриц, хранящих всю необходимую информацию о потоках на сети для аналитической реализации модели. Приведена классификация узловых точек сети. Предложены критерии оптимизации распределения потоков в узлах сети. Разработан алгоритм численного решения задачи определения оптимальных параметров регулирования для узловой точки II типа. С учетом граф-представления модели предложен методы определения оптимальной (из числа заданных) схемы распределения потоков по сети. Предлагаемая модель, ее граф-представление и методы решения оптимизационных задач могут быть применены не только к автотранспортной сети, но и к любой сетевой структуре при надлежащем выборе способа определения параметров распределения Эрланга.

Статья в формате PDF

973 KB

транспортная сеть

сетевые потоки

математическая модель

граф-представление

узловая точка

оптимизация

1. Наумова Н.А. Моделирование и программная реализация движения автотранспортных средств по улично-дорожной сети: монография / Н.А. Наумова, Л.М. Данович. – Краснодар: Издательский Дом – Юг, 2011. – 80 с.

2. Домбровский А.Н. Транспортные потоки на улично-дорожной сети городов: моделирование и управление: монография / А.Н. Домбровский, Н.А. Наумова; – Краснодар: Издательский Дом – Юг, 2012. – 124 с.

3. Cox D.R., Smith W.L., Queues, Methuen, London, 1961.

4. Drew D.R. Traffic Flow Theory and Control, McGraw-Hill Book Company. – New York, 1968.

5. Inose H., Hamada T., Road Traffic Control, University of Tokyo Press. – Tokyo, Japan, 1975.

Стремительный рост числа автовладельцев привел к значительному повышению объемов движения, частым транспортным заторам и увеличению себестоимости автомобильных перевозок. В связи с этим проблема рационального использования существующей улично-дорожной сети путем выбора оптимальной организации движения автотранспортных средств является очень актуальной.

Для эффективного управления потоками транспортной сети города и выбора оптимальных решений по проектированию транспортных сетей необходимо учитывать широкий спектр характеристик потока. Возникающие трудности связаны с нестабильностью транспортного потока и противоречивостью критериев качества управления движением. Время проезда по конкретному маршруту складывается из задержек на перекрестках и времени движения между перекрестками. Оптимизировать время движения между двумя пунктами улично-дорожной сети можно за счет сокращения потерь времени на перекрестках. Перспективной задачей является разработка микромодели транспортной динамики в узлах сети и оценка их влияния на распределение потоков по сети.

Представление транспортной сети в виде графа

Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое число. Поток на графе – это некоторая функция, заданная на дугах графа. В нашем случае поток на графе задается в виде функции плотности распределения интервалов по времени между требованиями. Будем считать распределение интервалов по времени в каждом из потоков требований (каналов) подчиненным распределению Эрланга:

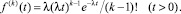(1)

Этот закон позволяет описывать потоки достаточно высокой плотности. В частности, для транспортных потоков гипотеза о распределении интервалов по времени между подряд идущими автомобилями по закону Эрланга подтверждается при интенсивности движения по каждой полосе до 500 авт./ч.

Назовем сетевые потоки неконфликтными, если на данном участке сети они не пересекаются, и конфликтными – в противном случае. Вершинами графа будем считать узловые точки – точки, в которых либо расположены источники или потребители информации, либо происходит пересечение конфликтных потоков. То есть узловые точки образуются пересечением многоканальных магистралей.

Рассмотрим узловую точку (УТ), в которой пересечение конфликтных потоков происходит следующим образом: одна часть потоков (назовем их главными) проходит через УТ беспрепятственно; требования второй части потоков (второстепенных) ожидают возникновения достаточных интервалов по времени между требованиями главных потоков для пересечения УТ. Назовем такую УТ узловой точкой первого типа (УТ I типа).

Узловую точку (УТ), в которой для возможности ее пересечения поочередно перекрывается движение для одной из групп неконфликтных потоков на фиксированное время Ti, назовем узловой точкой второго типа (УТ II типа).

Пусть {li} – множество дуг графа, {zi} – множество вершин (узловых точек). Дуга представляет собой часть многоканальной магистрали, заключенную между двумя вершинами (узловыми точками). Присвоим магистралям сети идентификационные номера WAY_i, i ∈ N. В этом случае

.

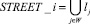Тогда можно представить граф с помощью следующих связанных матриц:

I.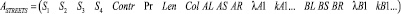

1) № – номер строки матрицы ASTREETS соответствует номеру дуги графа, соединяющей узловые точки I и II; количество строк соответствует количеству дуг графа;

2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;

3) S3 и S4 – пересекающиеся магистрали, образующие вершину II графа;

4) Contr – тип узловой точки;

5) Pr – наличие приоритета (главная или второстепенная магистраль);

6) Len – длина дуги между узловыми точками;

7) Col – количество потоков на дуге;

8) AL – допустимость поворота налево из направления А в вершине II;

9) AS – допустимость движения прямо из направления А вершине II;

10) AR – допустимость поворота направо из направления А вершине II;

11) λА1, λА2 и т.д. – параметр λ в направлении А;

12) kA1, kA2 и т.д. – параметр k в направлении А;

13) BL – допустимость поворота налево из направления В вершине I;

14) BS – допустимость движения прямо из направления В вершине I;

15) BR – допустимость поворота налево из направления В вершине I;

16) λВ1, λВ2 и т.д. – параметр λ в направлении В.

17) kB1, kB2 и т.д. – параметр k в направлении В.

II.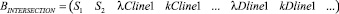

1) № строки совпадает с номером дуги графа, соединяющей узловые точки I и II в матрице ASTREETS ;

2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;

3) λCline1, λCline2 и т.д. –параметр λ потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;

4) kC line1, kC line2 и т.д. – параметр k потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;

5) λD line1, λD line2 и т.д. – параметр λ потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I;

6) kD line1, kD line2 и т.д. – параметр k потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I.

Определение оптимального распределения потоков в узловой точке

Рассмотрим следующую задачу: определить оптимальное (из множества

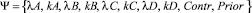
известных способов) распределение потоков для данной вершины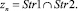

Критерием оптимизации, в зависимости от преследуемой цели, может служить:

1) 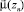 – вес вершины zn (узловой точки) для потока данного направления;

2) μ(zn) – вес вершины zn (узловой точки);

3) ωM(zn) – средняя задержка требования выбранных направлений.

Для узловой точки I типа:

1) 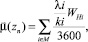 где М – множество выбранных направлений;

2) 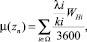 где Ω – множество всех направлений;

3) 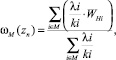 где М – множество выбранных направлений.

Здесь принято обозначение: Wн – средняя задержка (в секундах) в УТ одного требования второстепенного направления в потоке с параметрами распределения λ и k:

Для узловой точки II типа:

1) 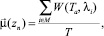 где М – множество выбранных направлений, a ∈ {1; 2};

2) 

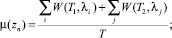
3) 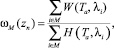 где М – множество выбранных направлений, a ∈ {1; 2}.

Здесь приняты обозначения:

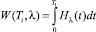(треб.∙с.) – суммарная задержка всех требований данного потока за один цикл регулирования T = T1 + T2;

H(t) – число требований, прибывающих к данной точке дороги за интервал времени (0; t).

Пусть задана вершина 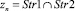(с точностью до порядка Str1 и Str2). Информация о входящих потоках содержится в матрицах ASTREETS и BINTERSECTION.

Лемма 1. Параметры распределения Эрланга, входящих в вершину 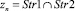потоков, заданы:

1) в матрице ASTREETS в строке

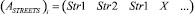– направление В;

2) в матрице BINTERSECTION в строке (BINTERSECTION)i в направлениях С и D;

3) в матрице ASTREETS в строке

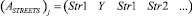– в направлении А.

Оптимальное распределение потоков в узловой точке является решением задачи (в зависимости от преследуемой цели):

1) 

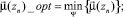
2) 

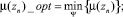
3) 

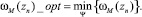
Выбор оптимальных параметров регулирования для узловой точки II типа

Поставим следующую задачу оптимизации функционирования узловой точки II типа: минимизировать суммарную часовую задержку μ(zn) всех требований в данном узле. При этом для каждого потока должно выполняться условие отсутствия затора:

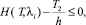i = 1, 2, ..., n1; (2)

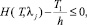j = 1, 2, ..., n2, (3)

где n1 – число потоков магистрали № 1; n2 – число потоков магистрали № 2. Кроме этого необходимо выполнение условия: T ≥ 2M, где М – минимальное время (в секундах), необходимое требованию для пересечения узловой точки II типа.

Задача математического (нелинейного) программирования имеет вид:

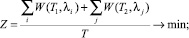(4)

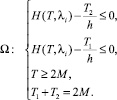(5)

В результате следует получить оптимальные значения параметров регулирования T1, T2.

Алгоритм численного решения задачи (4–5) зададим как релаксационный процесс – процесс построения последовательных приближений M1, M2, ..., Mk, ... таких, что Mi ∈ Ω и Z(Mk+1) < Z(Mk).

1-й шаг. Задаем начальные значения:

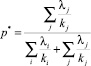
и 

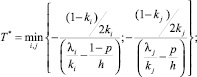
и значения для завершения алгоритма εp = 0,01; εT = 0,5; εZ = 0,1.

2-й шаг. Находим численно (например, методом половинного деления) решение уравнения 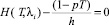, соответствующего условию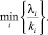

3-й шаг. Проверяем выполнение остальных неравенств системы ограничений:

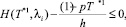i = 1, 2, ..., n1;

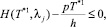j = 1, 2, ..., n2.

4-й шаг. Если условия шага 3 выполнены, вычисляем 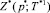и переходим к шагу 5.

Если условия шага 3 не выполнены, то находим численно (например, методом половинного деления) решение T*1 уравнения 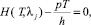соответствующего условию 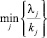; проверяем выполнение остальных неравенств системы ограничений:

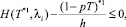i = 1, 2, ..., n1;

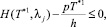j = 1, 2, ..., n2.

Затем вычисляем 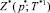и переходим к шагу 5.

5-й шаг. Приняв T = T*1 (начальное значение 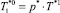) находим численно решение 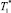уравнения:

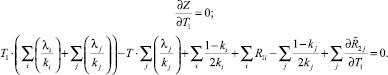
Тогда новое значение .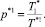

6-й шаг. Повторяем шаги 2–4 до тех пор, пока ΔZ < εz, Δp < εp, ΔT < εT.

Автором доказано, что последовательные приближения отвечают условиям сходимости к оптимальному решению M0:

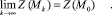
Определение критических значений параметров распределения Эрланга для узловой точки II типа

Как отмечено выше, «затор» в УТ II типа не образуется при выполнении условий (2‒3). В случае распределения интервалов по времени по закону Эрланга (1) данные условия равносильны следующей системе неравенств:

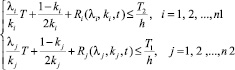(6)

Так как

,

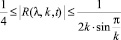то приближенное решение системы относительно параметра λ (при известном параметре k) следующее:

(7)

При необходимости значение параметра λ распределения Эрланга для каждого из потоков, гарантирующее отсутствие «заторов» в УТ II типа, может быть найдено численными методами с любой степенью точности путем решения (соответственно) уравнения:

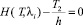
или

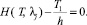(8)

Определение оптимальной (из числа заданных) схемы распределения потоков по сети

Пусть задан подграф {zn}n∈V, подлежащий реорганизации. Возможные варианты реорганизации распределения потоков на сети должны быть отражены в матрицах (ASTREETS)i и (BINTERSECTION)i , i ∈ K.

Если цель реорганизации – сведение к минимуму задержек в узловых точках, то критерий оптимизации – сумма весов узловых точек:

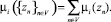
Оптимальная схема распределения потоков по сети является решением задачи:

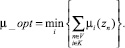
Если цель реорганизации – оптимизация движения потоков по данному маршруту (V, D) сети, то в качестве целевой функции следует взять

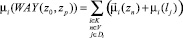
– вес маршрута, то есть время, затраченное на прохождение данного маршрута.

Здесь 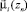– вес вершины zn (узловой точки) для потока данного направления;

μi(lj) – вес дуги lj для потока данного направления;

D – множество дуг маршрута;

V – множество вершин маршрута.

Тогда оптимальная схема распределения потоков является решением следующей задачи:

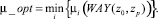
Заключение

Рассмотренные выше оптимизационные задачи базируются на гипотезе о распределении интервалов по времени между следующими подряд требованиями по закону Эрланга. Для транспортных потоков адекватность данной гипотезы проверена автором экспериментально. В работах [1–2] подробно рассматривается построение математической модели, построенной на гипотезе об эрланговском распределении интервалов по времени и ее аналитической реализации. Одной из положительных сторон модели является минимальное количество исходных данных, требующихся для расчетов показателей качества функционирования сети. Предложенное в данной работе граф-представление транспортной сети позволяет решать задачи по оптимизации распределения сетевых потоков. При наличии базы данных для конкретного участка улично-дорожной сети, построенной в соответствии со структурой матриц ASTREETS и BINTERSECTION, нетрудно осуществить компьютерную реализацию алгоритмов решения этих задач, например, в среде DELPHI.

Рецензенты:

Атрощенко В.А., д.т.н., профессор, декан факультета компьютерных технологий ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар;

Видовский Л.А., д.т.н., профессор, заведующий кафедрой вычислительной техники и автоматизированных систем управления ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.

Работа поступила в редакцию 07.11.2012.

Библиографическая ссылка